2026-01-25 00:56:33
I saw a post on X recently that said
Bill Gates is closer to you in wealth than he is to Elon Musk. Mind blown.
For round numbers, let’s say Elon Musk’s net worth is 800 billion and Bill Gates’ net worth is 100 billion. So if your net worth is less 450 billion, the statement in the post is true.
The reason the statement above is mind blowing is that in this context you naturally think on a logarithmic scale, even if you don’t know what a logarithm is.
Or to put it another way, we think in terms of orders of magnitude. Musk’s net worth is an order of magnitude greater than Gates’, and Gates’ net worth would be an order of magnitude greater than that of someone worth 10 billion. Musk is a notch above Gates, and Gates is a notch above someone with a net worth around 10 billion, where a “notch” is an order of magnitude.
To put it another way, we think in terms of geometric mean √ab rather than arithmetic mean (a + b)/2 in this context. 100 billion is the geometric mean between 12.5 billion and 800 billion. Geometric mean corresponds to the arithmetic mean on a log scale. And on this scale, Gates is closer to Musk than you are, unless you’re worth more than 12.5 billion.
Here are three more examples of geometric means.
The size of Jupiter is about midway between that of earth and the sun; it’s the geometric mean. On a linear scale Jupiter is much closer to the size of the earth than the sun, but on a logarithmic scale it’s about in the middle. More on that here.
The tritone (augmented fourth) is half an octave. So, for example, an F# is in the middle between a C and the C an octave higher. Its frequency is the geometric mean of the frequencies of the two C’s. More here.
Finally, the humans body is a middle-sized object in the universe. From Kevin Kelly:
Our body size is, weirdly, almost exactly in the middle of the size of the universe. The smallest things we know about are approximately 30 orders of magnitude smaller than we are, and the largest structures in the universe are about 30 orders of magnitude bigger.
The post Fortunes and Geometric Means first appeared on John D. Cook.2026-01-25 00:21:32
There is a way to prove that you know two numbers a and b, and their product c = ab, without revealing a, b, or c. This isn’t very exciting without more context — maybe you know that 7 × 3 = 21 — but it’s a building block of more interesting zero knowledge proofs, such as proving that a cryptocurrency transaction is valid without revealing the amount of the transaction.
The proof mechanism requires an elliptic curve G and a pairing of G with itself. (More on pairings shortly.) It also requires a generator g of the group structure on G.
The prover takes the three secret numbers and multiplies the generator g by each, encrypting the numbers as ag, bg, and cg. When G is a large elliptic curve, say one with on the order of 2256 points, then computing products like ag can be done quickly, but recovering a from g and ag is impractical. In a nutshell, multiplication is easy but division [1] is practically impossible [2].
The verifier receives ag, bg, and cg. How can he verify that ab = c without knowing a, b, or c? Here’s where pairing come in.
I go more into pairings here, but essentially a pairing is a mapping from two groups to a third group
e: G1 × G2 → GT
such that
e(aP, bQ) = e(P, Q)ab.
In our case G1 and G2 are both equal to the group G above, and the target group GT doesn’t matter for our discussion here. Also, P and Q will both be our generator g.
By the defining property of a pairing,
e(ag, bg) = e(g, g)ab
and
e(cg, g) = e(g, g)c.
So if ab = c, then e(g, g)ab and e(g, g)c will be equal.
[1] The literature will usually speak of discrete logarithms rather than division. The group structure on an elliptic curve is Abelian, and so it is usually written as addition. If you write the group operation as multiplication, then you’re taking logs rather than dividing. The multiplicative notation highlights the similarity to working in the multiplicative group modulo a large prime.
[2] The computation is theoretically possible but not possible in practice without spending enormous resources, or inventing a large scale quantum computer. This is the discrete logarithm assumption.
The post Proving you know a product first appeared on John D. Cook.2026-01-24 00:51:33
In a high school math class, the solution to the equation
bx = y
is the logarithm of y in base b. The implicit context of the equation is the real numbers, and the solution is easy to calculate.
The same problem in the context of finite groups is called the discrete logarithm problem, and it is difficult to solve for large groups. In particular, it is impractical to solve when working modulo a sufficiently large prime number or when working over a sufficiently large elliptic curve [1]. In either context, the exponential bx can be computed efficiently but its inverse cannot.
Now suppose you want to prove that you know x without revealing x itself. That is, you’d like to construct a zero knowledge proof that you know x. How could you do this?
Here’s one way.
Let’s see why this works.
First of all, what have you revealed to the prover? Two values: t and s. The value t is the exponential of a random number, and so another random number. The value s is based on x, and so conceivably you’ve revealed your secret. But the verifier does not know r, only a value computed from r (i.e. t) and the verifier cannot recover r from t because this would require computing a discrete logarithm.
Next, why should bs = t yc? Because
bs = br + cx = brbcx = t (bx)c = t yc.
Finally, why should the verifier believe you know x? If you don’t know x, but were able to come up with an s that satisfies the verifier, then you were able to compute the discrete logarithm of t yc.
[1] At least without a large-scale quantum computer. Schor’s algorithm could efficiently compute discrete logarithms if only there were a large quantum computer to run it on.
The post How to prove you know a discrete logarithm first appeared on John D. Cook.2026-01-21 23:27:57
The Mills ratio [1] is the ratio of the CCDF to the PDF. That is, for a random variable X, the Mills ratio at x is the complementary cumulative distribution function divided by the density function. If the density function of X is f, then
The Mills ratio highlights an important difference between the Student t distribution and the normal distribution.
Introductory statistics classes will say things like “you can approximate a t distribution with a normal if it has more than 30 degrees of freedom.” That may be true, depending on the application. A t(30) distribution and a normal distribution behave similarly in the middle but not in the tails.
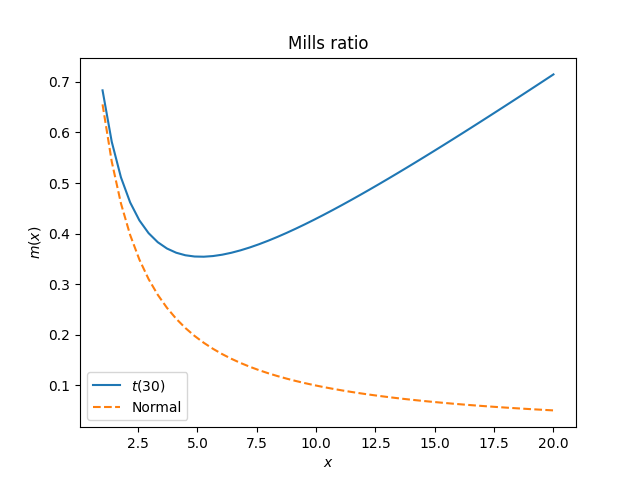
The Mills ratio for a t distribution with ν degrees of freedom is asymptotically x/ν, while the Mills ratio for a standard normal distribution is asymptotically 1/x. Note that increasing ν does make the Mills function smaller, but it still eventually grows linearly whereas the Mills function of a normal distribution decays linearly.
In general, the Mills ratio is a decreasing function for thin-tailed distributions and an increasing function for fat-tailed distributions. The exponential distribution is in the middle, with constant Mills function.
[1] Named after John P. Mills, so there’s no apostrophe before the s.
The post Mills ratio and tail thickness first appeared on John D. Cook.2026-01-21 21:20:49
I saw something yesterday saying that the Japanese bond market had experienced a six standard deviation move. This brought to mind a post I’d written eight years ago.
All probability statements depend on a model. And if you’re probability model says an event had a probability six standard deviations from the mean, it’s more likely that your model is wrong than that you’ve actually seen something that rare. I expand on this idea here.
How likely is it that a sample from a random variable will be six standard deviations from its mean? If you have in mind a normal (Gaussian) distribution, as most people do, then the probability is on the order of 1 chance in 10,000,000. Six sigma events are not common for any distribution, but they’re not unheard of for distributions with heavy tails.
Let X be a random variable with a Student t distribution and ν degrees of freedom. When ν is small, i.e. no more than 2, the tails of X are so fat that the standard deviation doesn’t exist. As ν → ∞ the Student t distribution approaches the normal distribution. So in some sense this distribution interpolates between fat tails and thin tails.
What is the probability that X takes on a value more than six standard deviations from its mean at 0, i.e. what does the function
f(ν) = Prob(X > 6σ)
look like as a function of ν where σ² = ν/(ν − 2) is the variance of X?
As you’d expect, the limit of f(ν) as ν → ∞ is the probability of a six-sigma event for a normal distribution, around 10−7 as mentioned above. Here’s a plot of f(ν) for ν > 3. Notice that the vertical axis is on a log scale, i.e. the probability decreases exponentially.
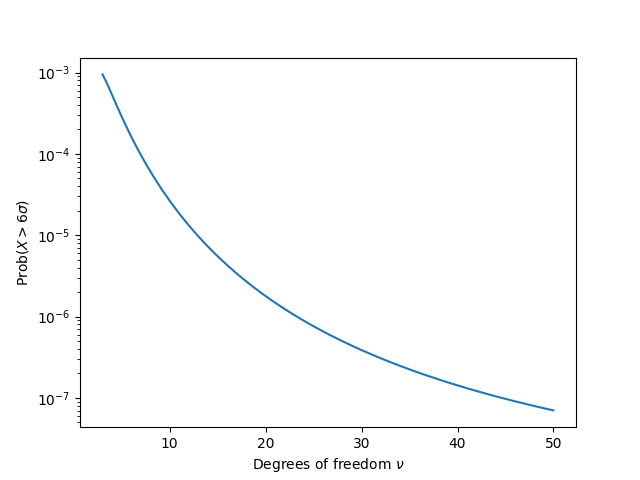
What you might not expect is that f(ν) isn’t monotone. It rises to a maximum value before it decays exponentially. In hindsight this makes sense. As ν → 2+ the variance becomes infinite, and the probability of being infinitely far from the mean is 0. Here’s a plot of f(ν) between 2 and 3.
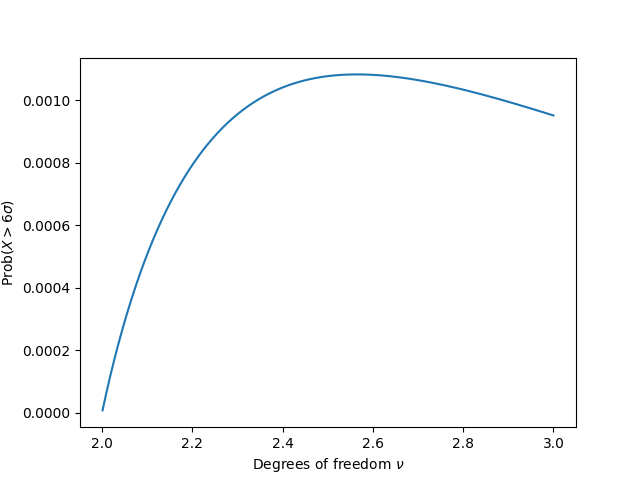
So six sigma probabilities for a Student t distribution rise from 0 up to a maximum of around 10−3 then decrease exponentially, then asymptotically approach a value around 10−7.
2026-01-20 23:10:02
I was reading an article this morning that mentioned a styometric analysis of a controversial paragraph written by Roman historian Flavius Josephus. I’ve written several posts that could be called stylometry or adjacent, but I haven’t used that word. Here are some posts that touch on the statistical analysis of a text or of an author.