2025-12-03 03:23:40
![]()
To immediately enable Wolfram Compute Services in Version 14.3 Wolfram Desktop systems, run
(The functionality is automatically available in the Wolfram Cloud.)
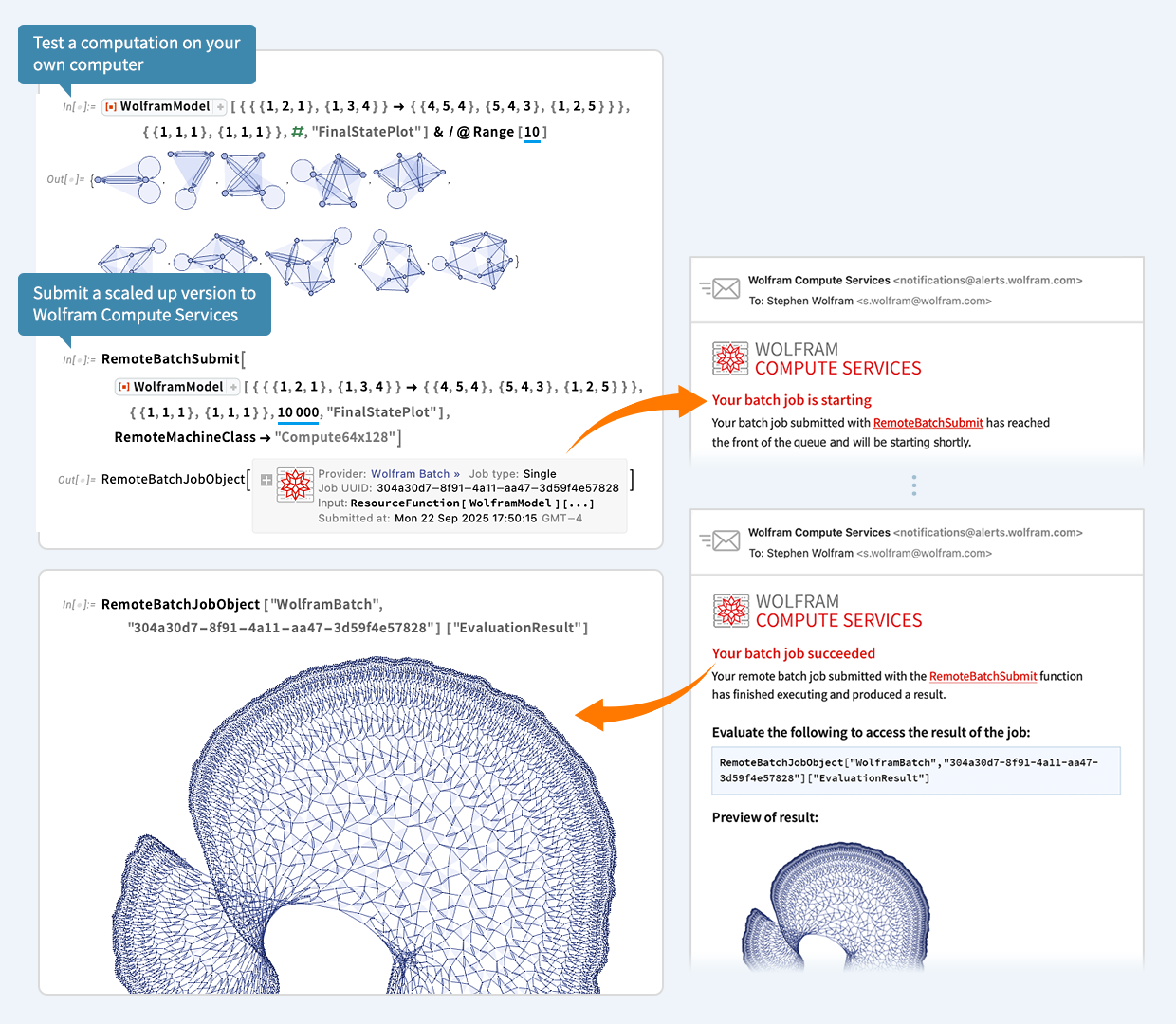
Let’s say you’ve done a computation in Wolfram Language. And now you want to scale it up. Maybe 1000x or more. Well, today we’ve released an extremely streamlined way to do that. Just wrap the scaled up computation in RemoteBatchSubmit and off it’ll go to our new Wolfram Compute Services system. Then—in a minute, an hour, a day, or whatever—it’ll let you know it’s finished, and you can get its results.
For decades I’ve often needed to do big, crunchy calculations (usually for science). With large volumes of data, millions of cases, rampant computational irreducibility, etc. I probably have more compute lying around my house than most people—these days about 200 cores worth. But many nights I’ll leave all of that compute running, all night—and I still want much more. Well, as of today, there’s an easy solution—for everyone: just seamlessly send your computation off to Wolfram Compute Services to be done, at basically any scale.
For nearly 20 years we’ve had built-in functions like ParallelMap and ParallelTable in Wolfram Language that make it immediate to parallelize subcomputations. But for this to really let you scale up, you have to have the compute. Which now—thanks to our new Wolfram Compute Services—everyone can immediately get.
The underlying tools that make Wolfram Compute Services possible have existed in the Wolfram Language for several years. But what Wolfram Compute Services now does is to pull everything together to provide an extremely streamlined all-in-one experience. For example, let’s say you’re working in a notebook and building up a computation. And finally you give the input that you want to scale up. Typically that input will have lots of dependencies on earlier parts of your computation. But you don’t have to worry about any of that. Just take the input you want to scale up, and feed it to RemoteBatchSubmit. Wolfram Compute Services will automatically take care of all the dependencies, etc.
And another thing: RemoteBatchSubmit, like every function in Wolfram Language, is dealing with symbolic expressions, which can represent anything—from numerical tables to images to graphs to user interfaces to videos, etc. So that means that the results you get can immediately be used, say in your Wolfram Notebook, without any importing, etc.
OK, so what kinds of machines can you run on? Well, Wolfram Compute Services gives you a bunch of options, suitable for different computations, and different budgets. There’s the most basic 1 core, 8 GB option—which you can use to just “get a computation off your own machine”. You can pick a machine with larger memory—currently up to about 1500 GB. Or you can pick a machine with more cores—currently up to 192. But if you’re looking for even larger scale parallelism Wolfram Compute Services can deal with that too. Because RemoteBatchMapSubmit can map a function across any number of elements, running on any number of cores, across multiple machines.
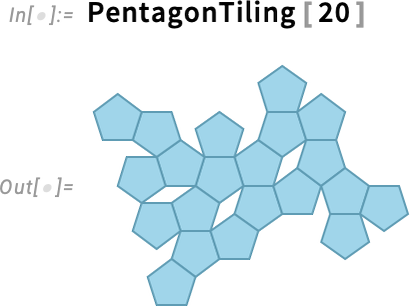
OK, so here’s a very simple example—that happens to come from some science I did a little while ago. Define a function PentagonTiling that randomly adds nonoverlapping pentagons to a cluster:

For 20 pentagons I can run this quickly on my machine:
But what about for 500 pentagons? Well, the computational geometry gets difficult and it would take long enough that I wouldn’t want to tie up my own machine doing it. But now there’s another option: use Wolfram Compute Services!
And all I have to do is feed my computation to RemoteBatchSubmit:

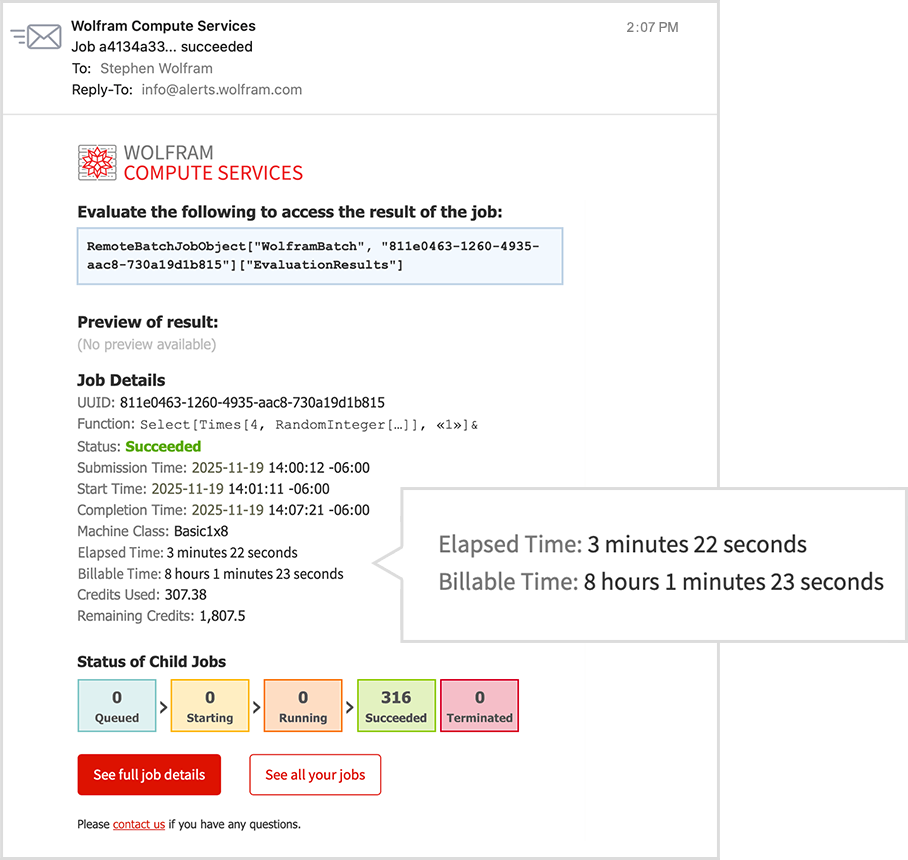
Immediately, a job is created (with all necessary dependencies automatically handled). And the job is queued for execution. And then, a couple of minutes later, I get an email:
Not knowing how long it’s going to take, I go off and do something else. But a while later, I’m curious to check how my job is doing. So I click the link in the email and it takes me to a dashboard—and I can see that my job is successfully running:
I go off and do other things. Then, suddenly, I get an email:
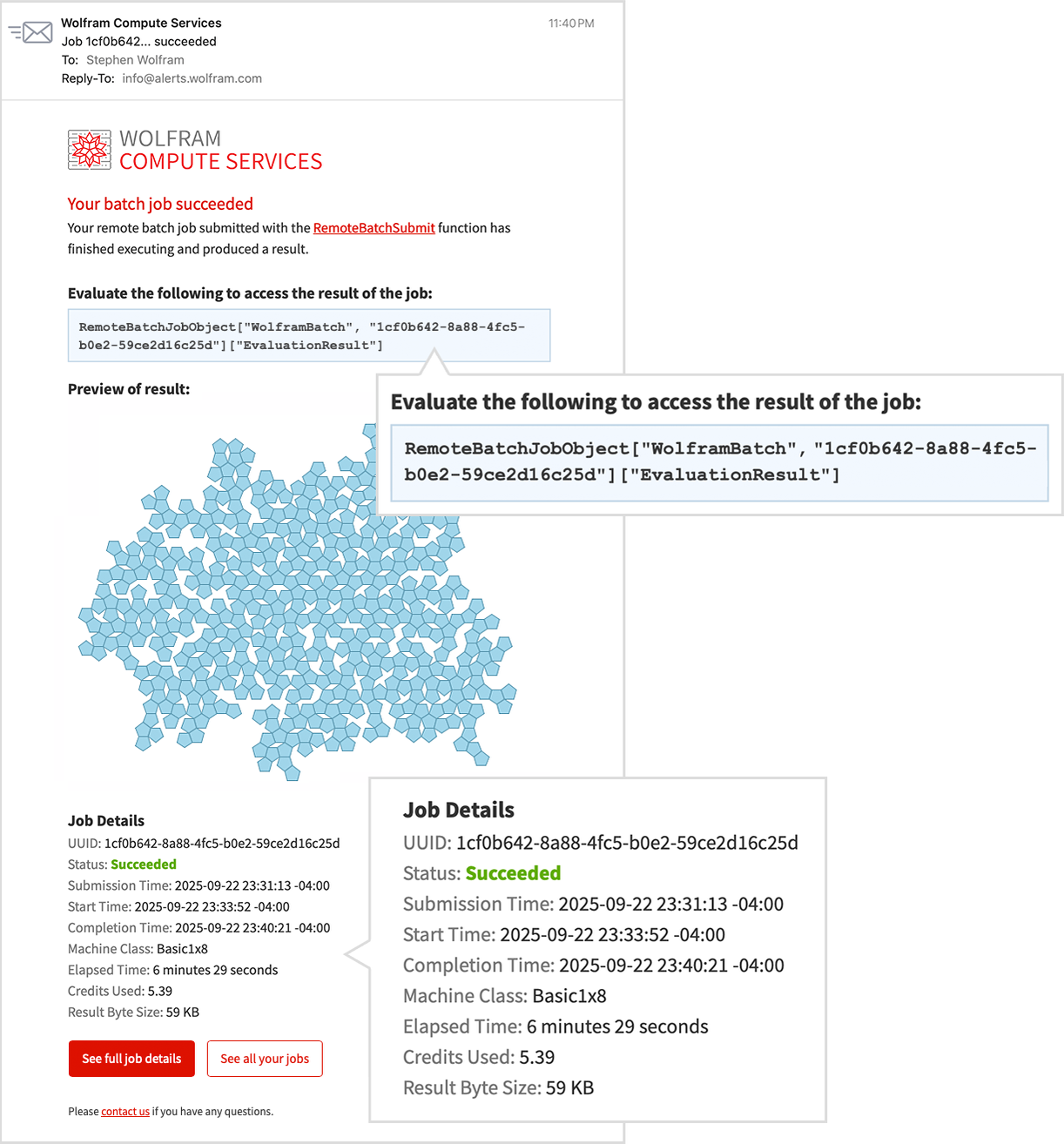
It finished! And in the mail is a preview of the result. To get the result as an expression in a Wolfram Language session I just evaluate a line from the email:

And this is now a computable object that I can work with, say computing areas
or counting holes:
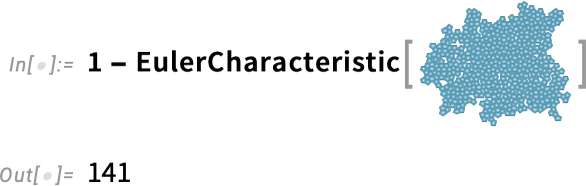
One of the great strengths of Wolfram Compute Services is that it makes it easy to use large-scale parallelism. You want to run your computation in parallel on hundreds of cores? Well, just use Wolfram Compute Services!
Here’s an example that came up in some recent work of mine. I’m searching for a cellular automaton rule that generates a pattern with a “lifetime” of exactly 100 steps. Here I’m testing 10,000 random rules—which takes a couple of seconds, and doesn’t find anything:
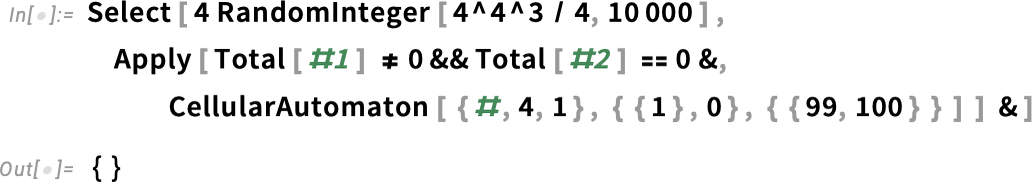
To test 100,000 rules I can use ParallelSelect and run in parallel, say across the 16 cores in my laptop:
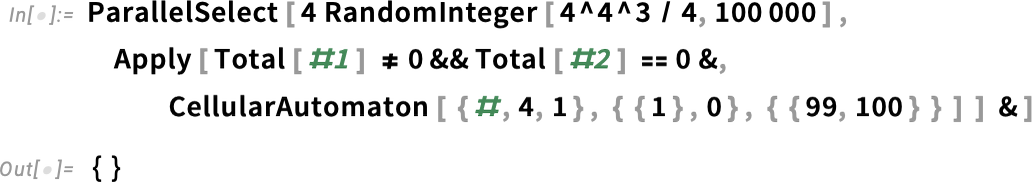
Still nothing. OK, so what about testing 100 million rules? Well, then it’s time for Wolfram Compute Services. The simplest thing to do is just to submit a job requesting a machine with lots of cores (here 192, the maximum currently offered):
A few minutes later I get mail telling me the job is starting. After a while I check on my job and it’s still running:
I go off and do other things. Then, after a couple of hours I get mail telling me my job is finished. And there’s a preview in the email that shows, yes, it found some things:

I get the result:

And here they are—rules plucked from the hundred million tests we did in the computational universe:

But what if we wanted to get this result in less than a couple of hours? Well, then we’d need even more parallelism. And, actually, Wolfram Compute Services lets us get that too—using RemoteBatchMapSubmit. You can think of RemoteBatchMapSubmit as a souped up analog of ParallelMap—mapping a function across a list of any length, splitting up the necessary computations across cores that can be on different machines, and handling the data and communications involved in a scalable way.
Because RemoteBatchMapSubmit is a “pure Map” we have to rearrange our computation a little—making it run 100,000 cases of selecting from 1000 random instances:
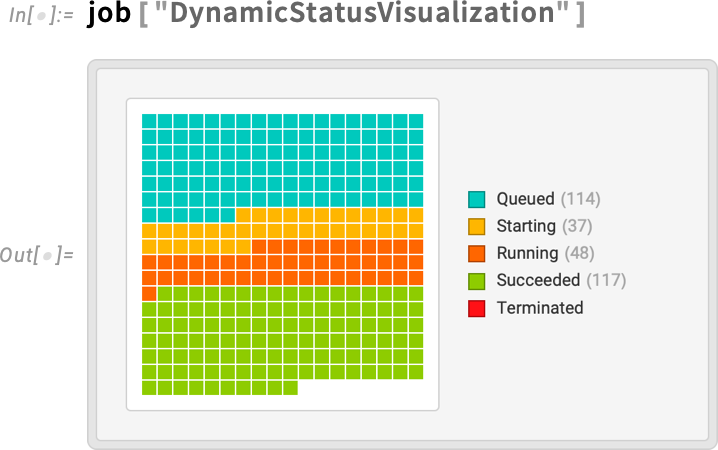
The system decided to distribute my 100,000 cases across 316 separate “child jobs”, here each running on its own core. How is the job doing? I can get a dynamic visualization of what’s happening:
And it doesn’t take many minutes before I’m getting mail that the job is finished:
And, yes, even though I only had to wait for 3 minutes to get this result, the total amount of computer time used—across all the cores—is about 8 hours.
Now I can retrieve all the results, using Catenate to combine all the separate pieces I generated:

And, yes, if I wanted to spend a little more, I could run a bigger search, increasing the 100,000 to a larger number; RemoteBatchMapSubmit and Wolfram Compute Services would seamlessly scale up.
Like everything around Wolfram Language, Wolfram Compute Services is fully programmable. When you submit a job, there are lots of options you can set. We already saw the option RemoteMachineClass which lets you choose the type of machine to use. Currently the choices range from "Basic1x8" (1 core, 8 GB) through "Basic4x16" (4 cores, 16 GB) to “parallel compute” "Compute192x384" (192 cores, 384 GB) and “large memory” "Memory192x1536" (192 cores, 1536 GB).
Different classes of machine cost different numbers of credits to run. And to make sure things don’t go out of control, you can set the options TimeConstraint (maximum time in seconds) and CreditConstraint (maximum number of credits to use).
Then there’s notification. The default is to send one email when the job is starting, and one when it’s finished. There’s an option RemoteJobName that lets you give a name to each job, so you can more easily tell which job a particular piece of email is about, or where the job is on the web dashboard. (If you don’t give a name to a job, it’ll be referred to by the UUID it’s been assigned.)
The option RemoteJobNotifications lets you say what notifications you want, and how you want to receive them. There can be notifications whenever the status of a job changes, or at specific time intervals, or when specific numbers of credits have been used. You can get notifications either by email, or by text message. And, yes, if you get notified that your job is going to run out of credits, you can always go to the Wolfram Account portal to top up your credits.
There are many properties of jobs that you can query. A central one is "EvaluationResult". But, for example, "EvaluationData" gives you a whole association of related information:

If your job succeeds, it’s pretty likely "EvaluationResult" will be all you need. But if something goes wrong, you can easily drill down to study the details of what happened with the job, for example by looking at "JobLogTabular".
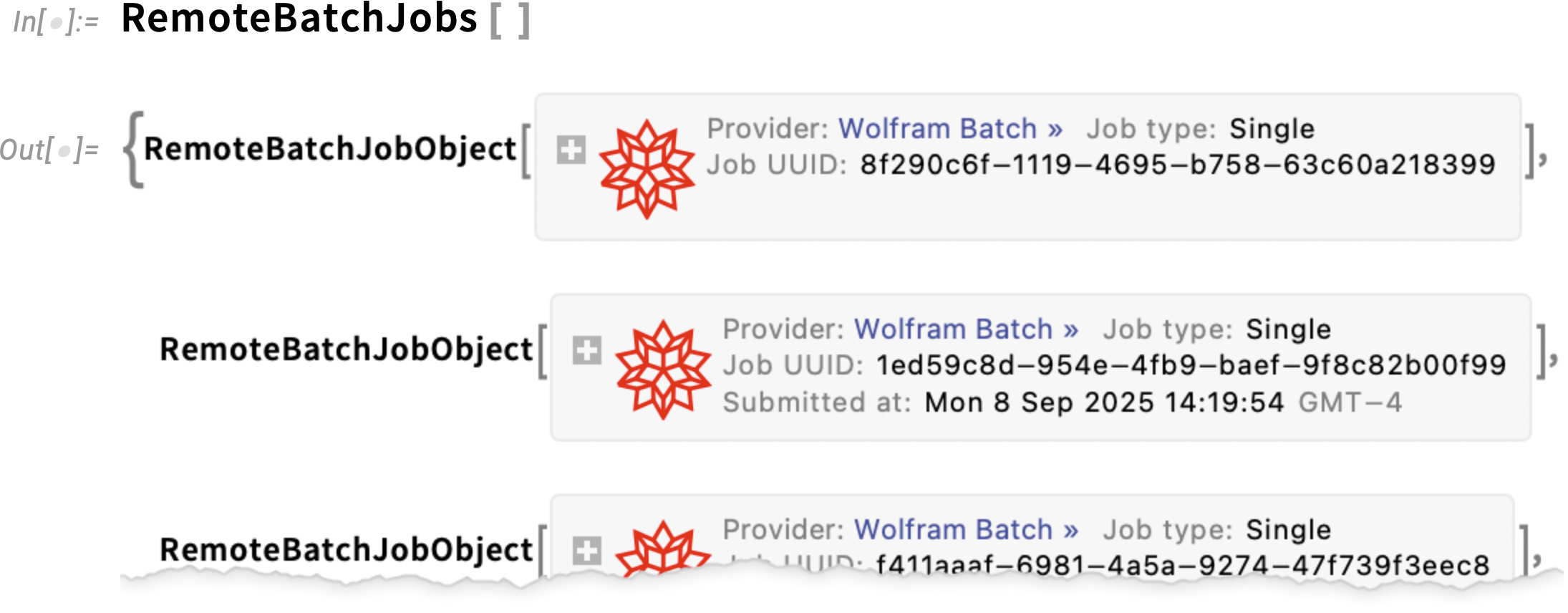
If you want to know all the jobs you’ve initiated, you can always look at the web dashboard, but you can also get symbolic representations of the jobs from:
For any of these job objects, you can ask for properties, and you can for example also apply RemoteBatchJobAbort to abort them.
Once a job has completed, its result will be stored in Wolfram Compute Services—but only for a limited time (currently two weeks). Of course, once you’ve got the result, it’s very easy to store it permanently, for example, by putting it into the Wolfram Cloud using CloudPut[expr]. (If you know you’re going to want to store the result permanently, you can also do the CloudPut right inside your RemoteBatchSubmit.)
Talking about programmatic uses of Wolfram Compute Services, here’s another example: let’s say you want to generate a compute-intensive report once a week. Well, then you can put together several very high-level Wolfram Language functions to deploy a scheduled task that will run in the Wolfram Cloud to initiate jobs for Wolfram Compute Services:
And, yes, you can initiate a Wolfram Compute Services job from any Wolfram Language system, whether on the desktop or in the cloud.
Wolfram Compute Services is going to be very useful to many people. But actually it’s just part of a much larger constellation of capabilities aimed at broadening the ways Wolfram Language can be used.
Mathematica and the Wolfram Language started—back in 1988—as desktop systems. But even at the very beginning, there was a capability to run the notebook front end on one machine, and then have a “remote kernel” on another machine. (In those days we supported, among other things, communication via phone line!) In 2008 we introduced built-in parallel computation capabilities like ParallelMap and ParallelTable. Then in 2014 we introduced the Wolfram Cloud—both replicating the core functionality of Wolfram Notebooks on the web, and providing services such as instant APIs and scheduled tasks. Soon thereafter, we introduced the Enterprise Private Cloud—a private version of Wolfram Cloud. In 2021 we introduced Wolfram Application Server to deliver high-performance APIs (and it’s what we now use, for example, for Wolfram|Alpha). Along the way, in 2019, we introduced Wolfram Engine as a streamlined server and command-line deployment of Wolfram Language. Around Wolfram Engine we built WSTPServer to serve Wolfram Engine capabilities on local networks, and we introduced WolframScript to provide a deployment-agnostic way to run command-line-style Wolfram Language code. In 2020 we then introduced the first version of RemoteBatchSubmit, to be used with cloud services such as AWS and Azure. But unlike with Wolfram Compute Services, this required “do it yourself” provisioning and licensing with the cloud services. And, finally, now, that’s what we’ve automated in Wolfram Compute Services.
OK, so what’s next? An important direction is the forthcoming Wolfram HPCKit—for organizations with their own large-scale compute facilities to set up their own back ends to RemoteBatchSubmit, etc. RemoteBatchSubmit is built in a very general way, that allows different “batch computation providers” to be plugged in. Wolfram Compute Services is initially set up to support just one standard batch computation provider: "WolframBatch". HPCKit will allow organizations to configure their own compute facilities (often with our help) to serve as batch computation providers, extending the streamlined experience of Wolfram Compute Services to on-premise or organizational compute facilities, and automating what is often a rather fiddly job process of submission (which, I must say, personally reminds me a lot of the mainframe job control systems I used in the 1970s).
Wolfram Compute Services is currently set up purely as a batch computation environment. But within the Wolfram System, we have the capability to support synchronous remote computation, and we’re planning to extend Wolfram Compute Services to offer this—allowing one, for example, to seamlessly run a remote kernel on a large or exotic remote machine.
But this is for the future. Today we’re launching the first version of Wolfram Compute Services. Which makes “supercomputer power” immediately available for any Wolfram Language computation. I think it’s going to be very useful to a broad range of users of Wolfram Language. I know I’m going to be using it a lot.
2025-11-11 23:19:17
![]()

It’s a key feature of living systems, perhaps even in some ways the key feature: that even right down to a molecular scale, things are orchestrated. Molecules (or at least large ones) don’t just move around randomly, like in a liquid or a gel. Instead, what molecular biology has discovered is that there are endless active mechanisms that in effect orchestrate what even individual molecules in living systems do. But what is the result of all that orchestration? And could there perhaps be a general characterization of what happens in systems that exhibit such “bulk orchestration”? I’ve been wondering about these questions for some time. But finally now I think I may have the beginnings of some answers.
The central idea is to consider the effect that “being adapted for an overall purpose” has on the underlying operation of a system. At the outset, one might imagine that there’d be no general answer to this, and that it would always depend on the specifics of the system and the purpose. But what we’ll discover is that there is in fact typically a certain universality in what happens. Its ultimate origin is the Principle of Computational Equivalence and certain universal features of the phenomenon of computational irreducibility that it implies. But the point is that so long as a purpose is somehow “computationally simple” then—more or less regardless of what in detail the purpose is—a system that achieves it will show certain features in its behavior.
Whenever there’s computational irreducibility we can think of it as exerting a powerful force towards unpredictability and randomness (as it does, for example, in the Second Law of thermodynamics). So for a system to achieve an overall “computationally simple purpose” this computational irreducibility must in some sense be tamed, or at least contained. And in fact it’s an inevitable feature of computational irreducibility that within it there must be “pockets of computational reducibility” where simpler behavior occurs. And at some level the way computationally simple purposes must be achieved is by tapping into those pockets of reducibility.
When there’s computational irreducibility it means that there’s no simple narrative one can expect to give of how a system behaves, and no overall “mechanism” one can expect to identify for it. But one can think of pockets of computational reducibility as corresponding to at least small-scale “identifiable mechanisms”. And what we’ll discover is that when there’s a “simple overall purpose” being achieved these mechanisms tend to become more manifest. And this means that when a system is achieving an overall purpose there’s a trace of this even down in the detailed operation of the system. And that trace is what I’ve called “mechanoidal behavior”—behavior in which there are at least small-scale “mechanism-like phenomena” that we can think of as acting together through “bulk orchestration” to achieve a certain overall purpose.
The concept that there might be universal features associated with the interplay between some kind of overall simplicity and underlying computational irreducibility is something not unfamiliar. Indeed, in various forms it’s the ultimate key to our recent progress in the foundations of physics, mathematics and, in fact, biology.
In our effort to get a general understanding of bulk orchestration and the behavior of systems that “achieve purposes” there’s an analogy we can make to statistical mechanics. One might have imagined that to reach conclusions about, say, gases, we’d have to have detailed information about the motion of molecules. But in fact we know that if we just consider the whole ensemble of possible configurations of molecules, then by taking statistical averages we can deduce all sorts of properties of gases. (And, yes, the foundational reason this works we can now understand in terms of computational irreducibility, etc.)
So could we perhaps do something similar for bulk orchestration? Is there some ensemble we can identify in which wherever we look there will with overwhelming probability be certain properties? In the statistical mechanics of gases we imagine that the underlying laws of mechanics are fixed, but there’s a whole ensemble of possible initial configurations for the molecules—almost all of which turn out to have the same limiting features. But in biology, for example, we can think of different genomes as defining different rules for the development and operation of organisms. And so now what we want is a new kind of ensemble—that we can call a rulial ensemble: an ensemble of possible rules.
But in something like biology, it’s not all possible rules we want; rather, it’s rules that have been selected to “achieve the purpose” of making a successful organism. We don’t have a general way to characterize what defines biological fitness. But the key point here is that at a fundamental level we don’t need that. Instead it seems that just knowing that our fitness function is somehow computationally simple tells us enough to be able to deduce properties of our “rulial ensemble”.
But are the fitness functions of biology in fact computationally simple? I’ve recently argued that their simplicity is precisely what makes biological evolution possible. Like so many other foundational phenomena, it seems that biological evolution is a reflection of the interplay between computational simplicity—in the case of fitness functions—and underlying computational irreducibility. (In effect, organisms have a chance only because the problems they have to solve aren’t too computationally difficult.) But now we can use the simplicity of fitness functions—without knowing any more details about them—to make conclusions about the relevant rulial ensemble, and from there to begin to derive general principles associated with bulk orchestration.
When one describes why a system does what it does, there are two different approaches one can take. One can go from the bottom up and describe the underlying rules by which the system operates (in effect, its “mechanism”). Or one can go from the top down and describe what the system “achieves” (in effect, its “goal” or “purpose”). It tends to be difficult to mix these two approaches. But what we’re going to find here is that by thinking in terms of the rulial ensemble we will be able to see the general pattern of both the “upward” effect of underlying rules, and the “downward” effect of overall purposes.
What I’ll do here is just a beginning—a first exploration, both computational and conceptual, of the rulial ensemble and its consequences. But already there seem to be strong indications that by thinking in terms of the rulial ensemble one may be able to develop what amounts to a foundational theory of bulk orchestration, and with it a foundational theory of certain aspects of adaptive systems, and most notably biology.
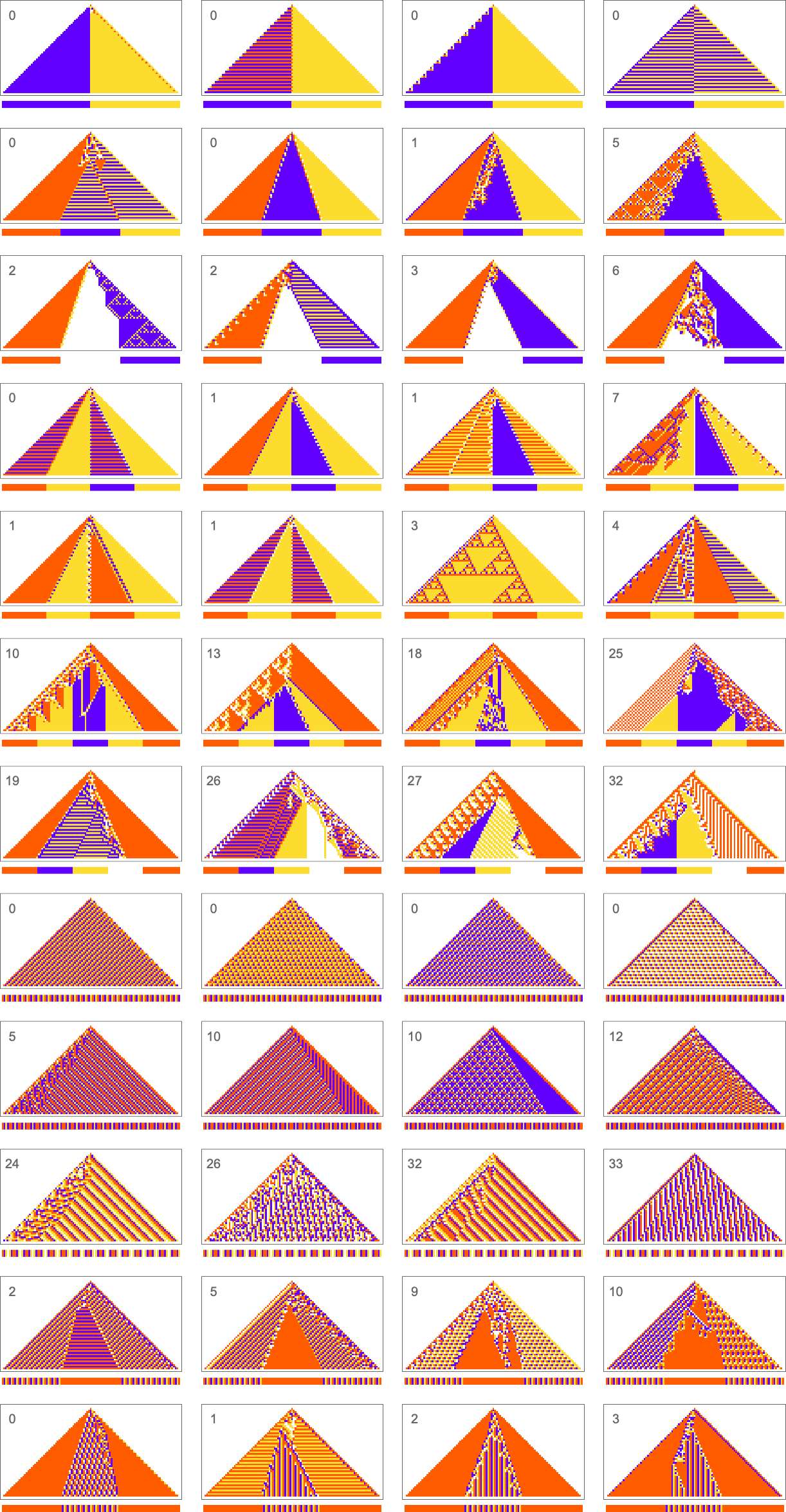
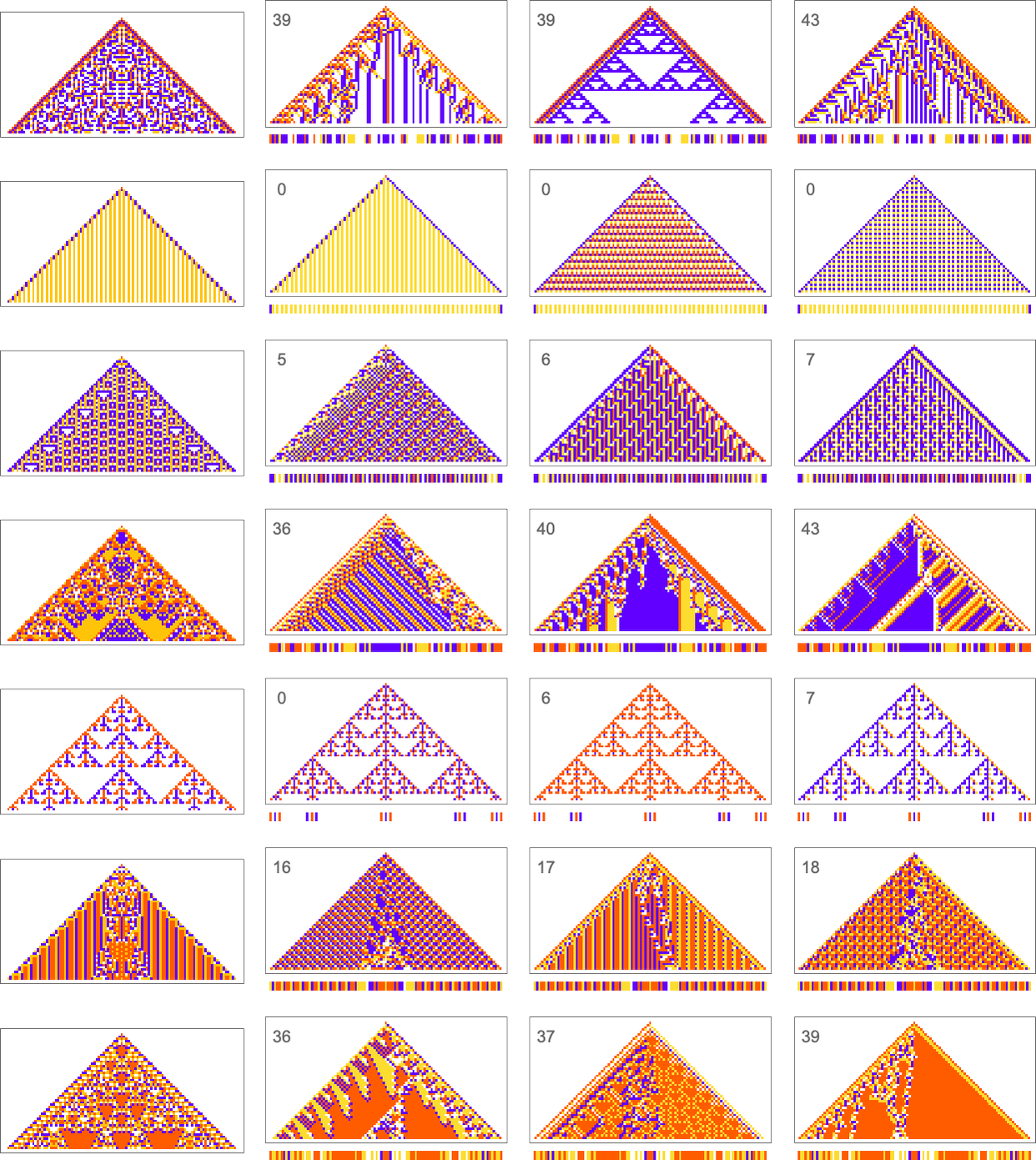
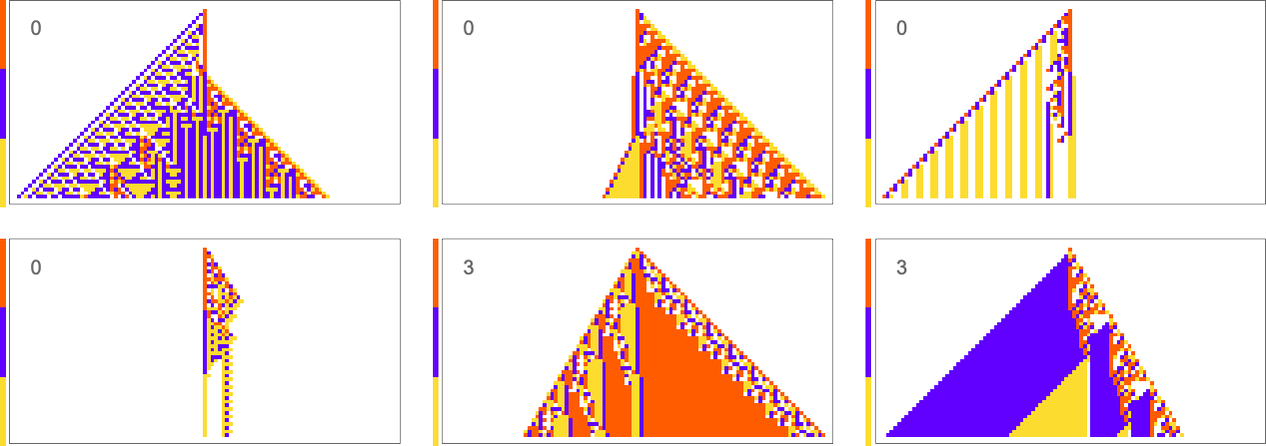
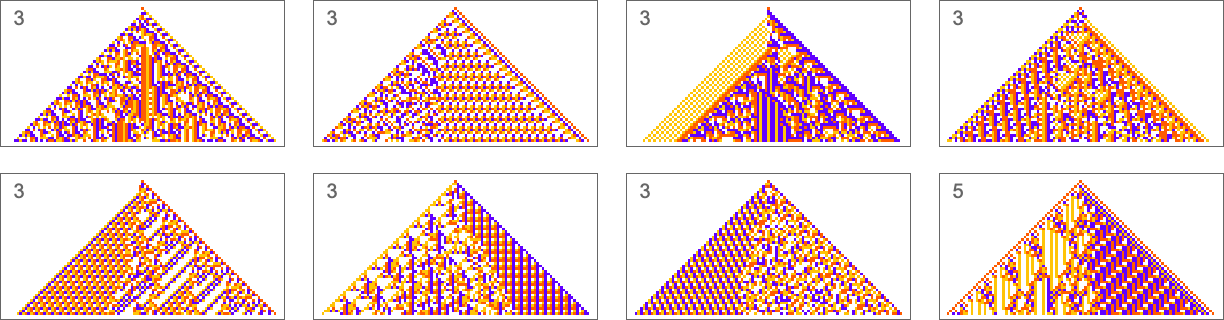
To begin our explorations and start developing our intuition let’s look at a few simple examples. We’ll use the same basic framework as in my recent work on biological evolution. The idea is to have cellular automata whose rules serve as an idealization of genotypes, and whole behavior serves as an idealization of the development of phenotypes. For our fitness function we’re going to start with something very specific: that after 50 steps (starting from a single-cell “seed”) our cellular automaton should generate “output” that consists of three equal blocks of cells colored red, blue and yellow.
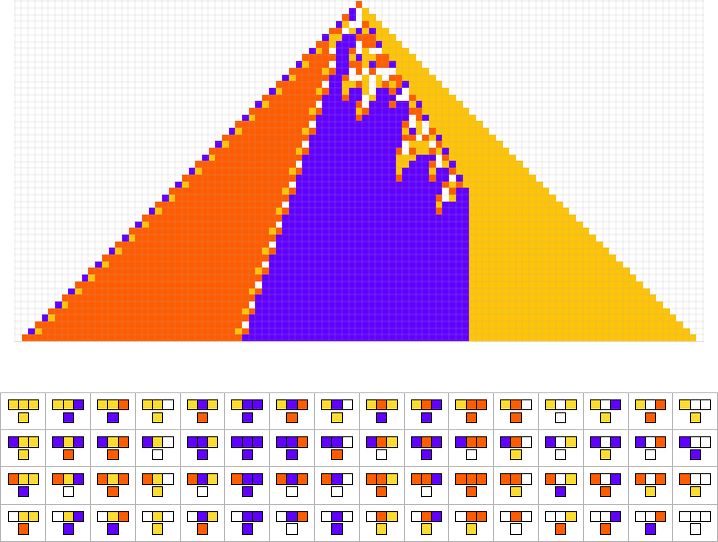
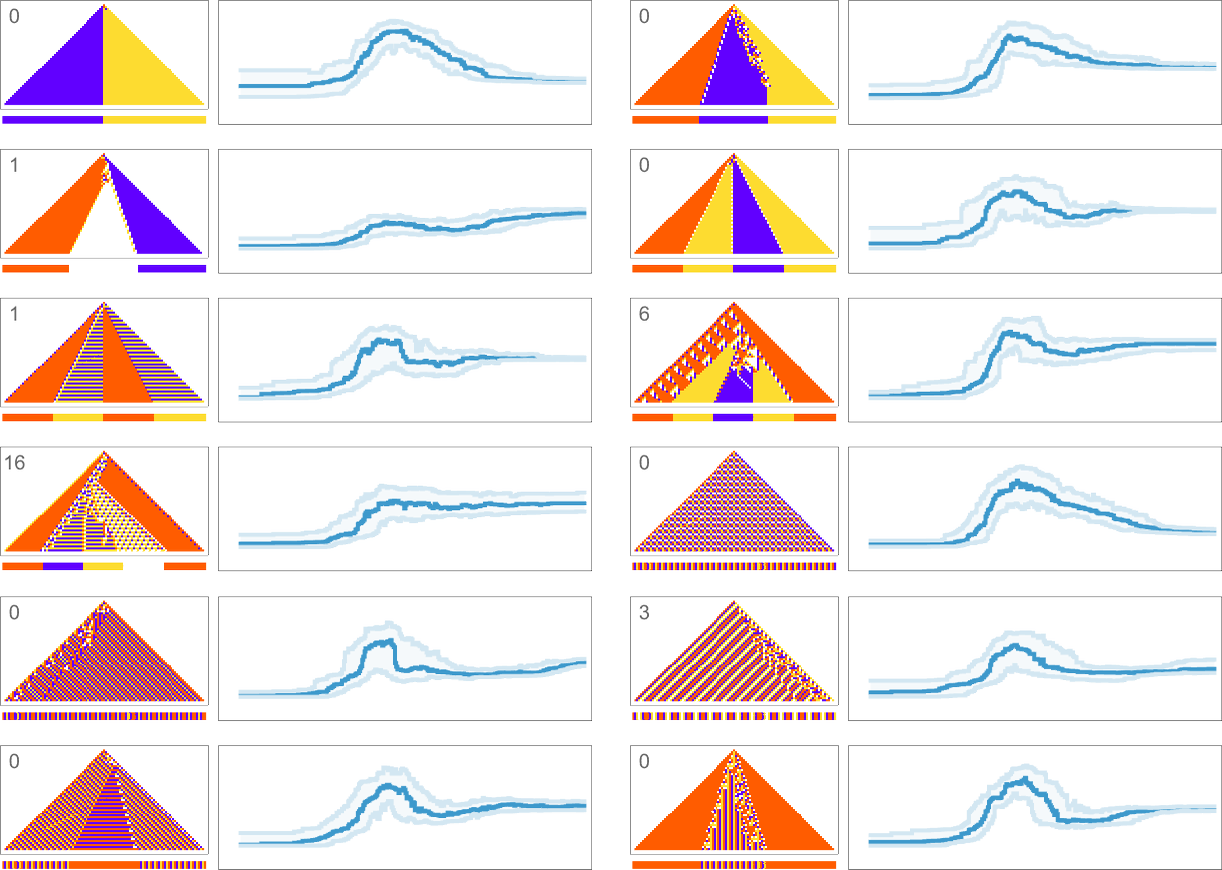
Here are some examples of rules that “solve this particular problem”, in various different ways:
How can such rules be found? Well, we can use an idealization of biological evolution. Let’s consider the first rule above:
We start, say, from a null rule, then make successive random point mutations in the rule
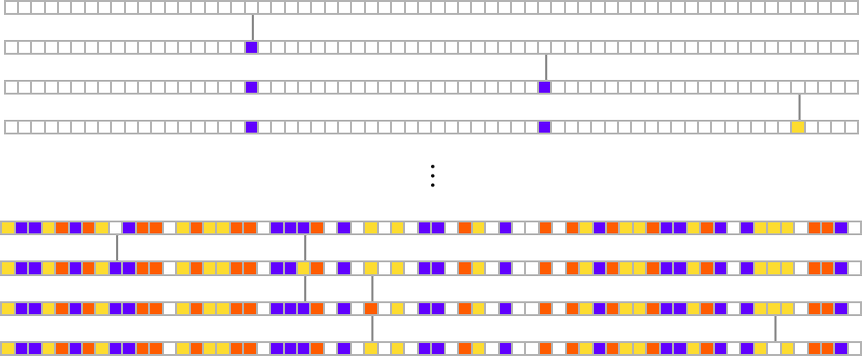
keeping those mutations that don’t take us further from achieving our goal (and dropping those that do, each indicated here by a red dot):
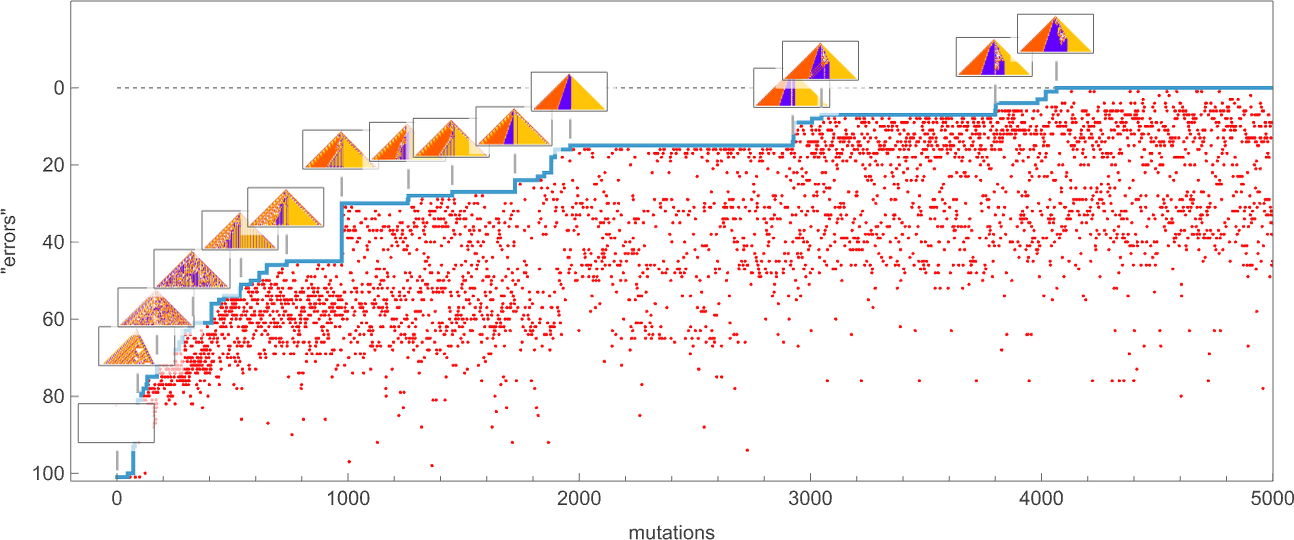
The result is that we “progressively adapt” over the course of a few thousand mutations to successively reduce the number of “errors” and eventually (and in this case, perfectly) achieve our goal:
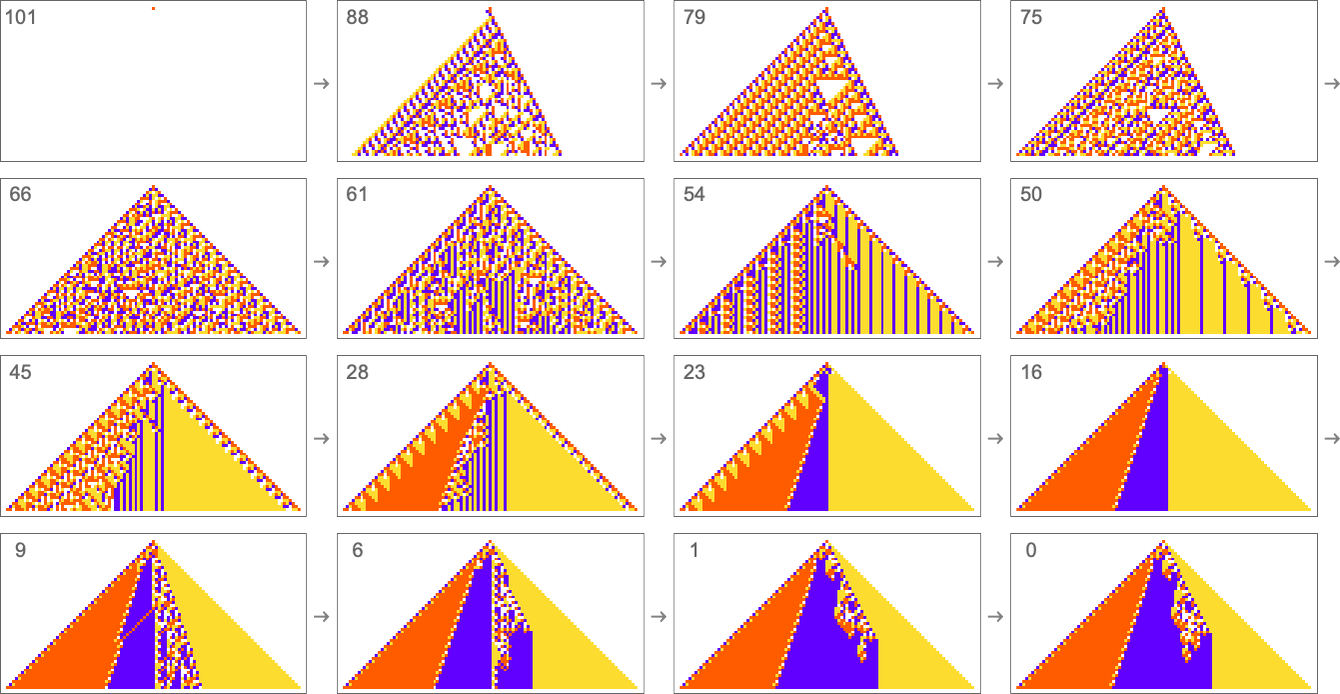
Early in this sequence there’s lots of computational irreducibility in evidence. But in the process of adapting to achieve our goal the computational irreducibility progressively gets “contained” and in effect squeezed out, until eventually the final solution in this case has an almost completely simple structure.
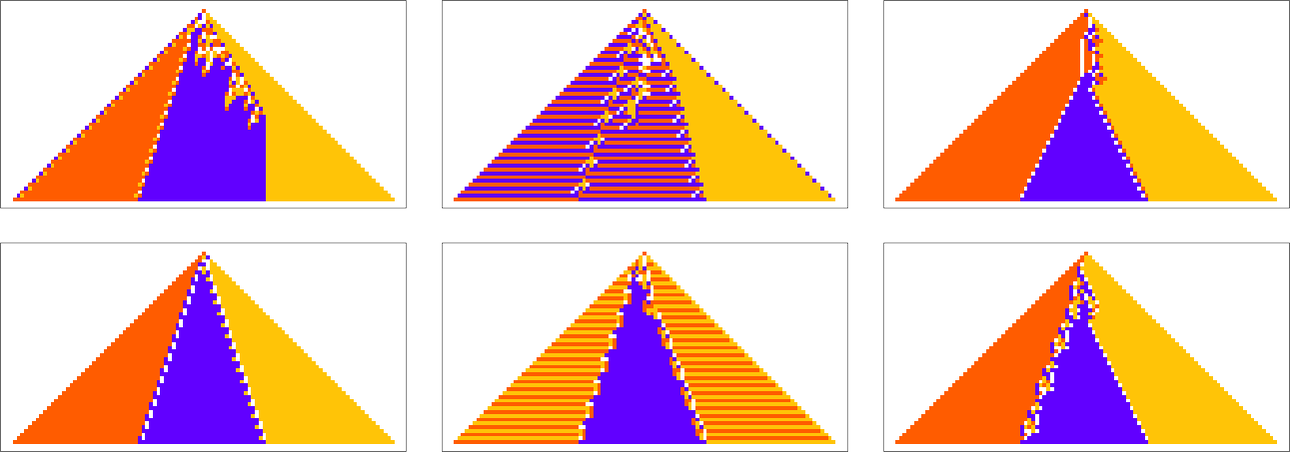
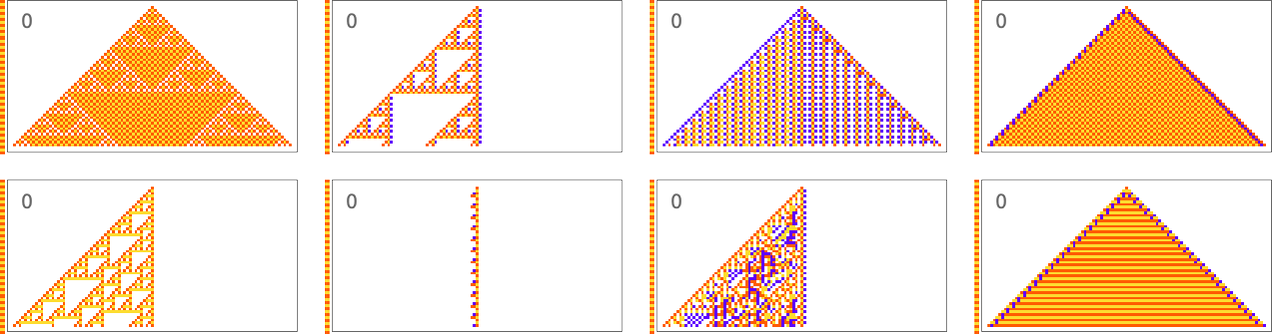
The example we’ve just seen succeeds in exactly achieving the objective we defined—though it takes about 4000 steps of adaptive evolution to do so. But if we limit the number of steps of adaptive evolution then in general we won’t be able to reach the exact objective we’ve defined. But here are some results we get with 10,000 steps of adaptive evolution (sorted by how close they get):
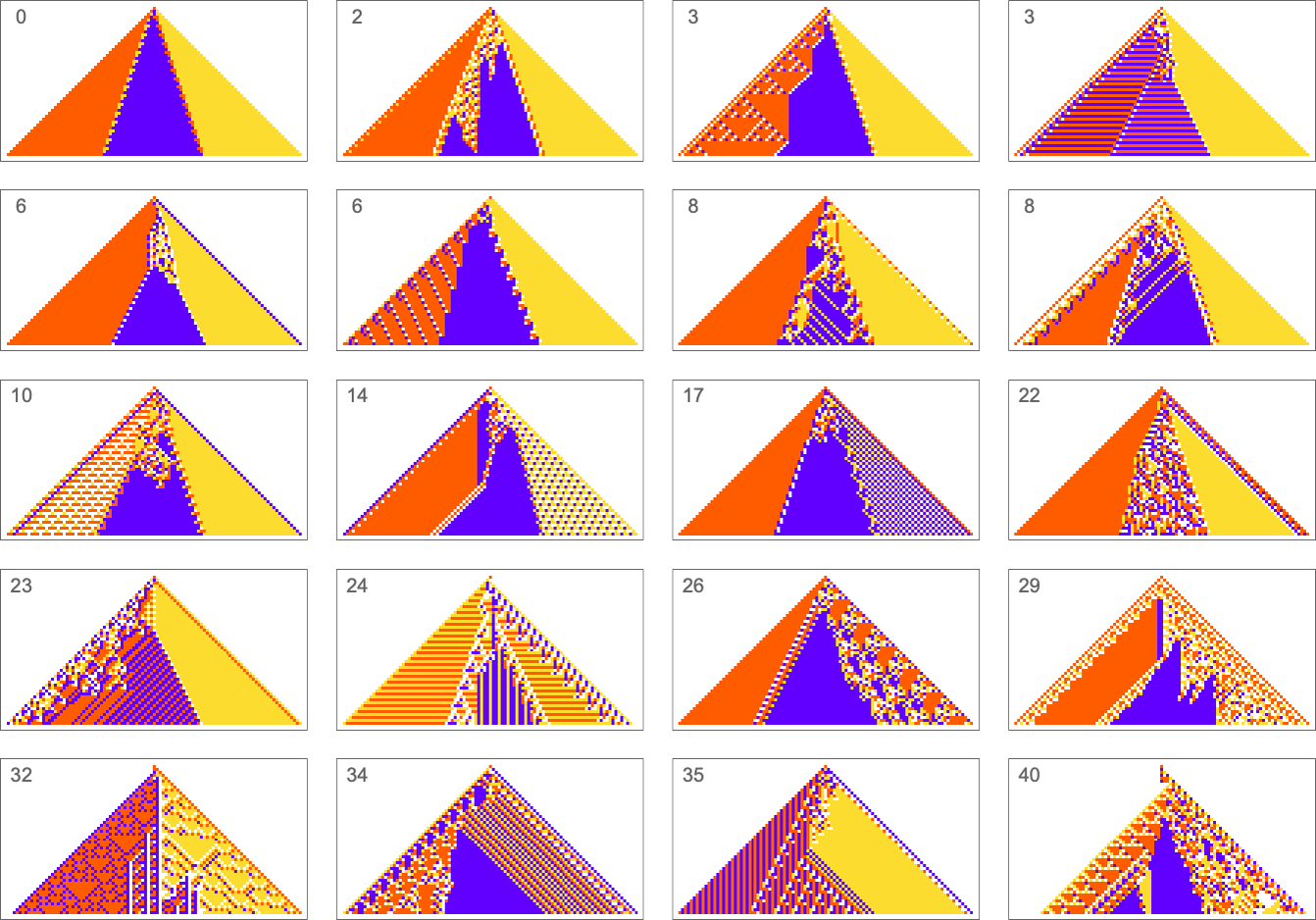
In all cases there’s a certain amount of “identifiable mechanism” to what these rules do. Yes, there can be patches of complex—and presumably computationally irreducible—behavior. But particularly the rules that do better at achieving our exact objective tend to “keep this computational irreducibility at bay”, and emphasize their “simple mechanisms”.
So what we see is that among all possible rules, those that get even close to achieving the “purpose” we have set in effect show at least “patches of mechanism”. In other words, the imposition of a purpose selects out rules that “exhibit mechanism”, and show what we’ve called mechanoidal behavior.
In the last section we saw that adaptive evolution can find (4-color) cellular automaton rules that generate the particular ![]() output we specified. But what about other kinds of output?
output we specified. But what about other kinds of output?
What we manage to get will depend on how much “effort” of adaptive evolution we put in. If we limit ourselves to 10,000 steps of adaptive evolution here are some examples of what happens:
At a qualitative level the main takeaway here is that it seems that the “simpler” the objective is, the more closely it’s likely to be achieved by a given number of steps of adaptive evolution.
Looking at the first (i.e. “ultimately most successful”) examples above, here’s how they’re reached in the course of adaptive evolution:
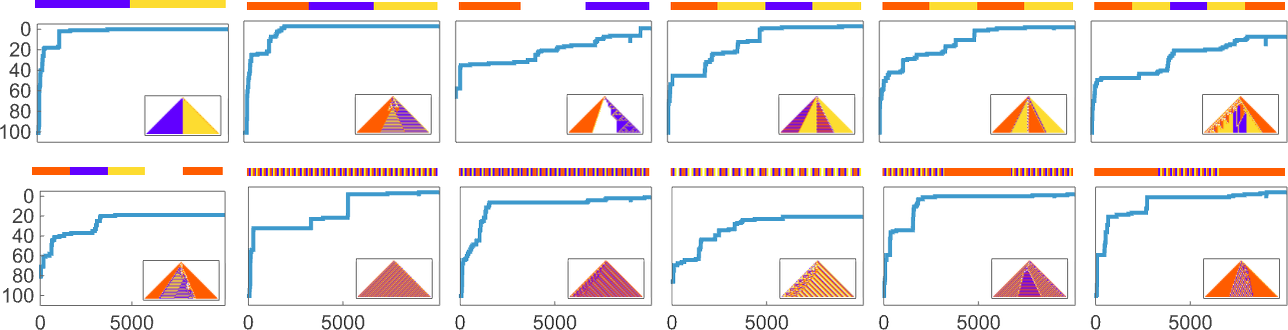
And we see that the “simpler” sequences are reached both more successfully and more quickly; in effect they seem to be “easier” for adaptive evolution to generate.
But what do we mean by “simpler” here? In qualitative terms we can think of the “simplicity” of a sequence as being characterized by how short a description we can find of it. We might try to compress the sequence, say using some standard practical compression technique, like run-length encoding, block encoding or dictionary encoding. And for the sequences we’re using above, these will (mostly) agree about what’s simpler and what’s not. And then what we find is that sequences that are “simpler” in this kind of characterization tend to be ones that are easier for adaptive evolution to produce.
But, actually, our study of adaptive evolution itself gives us a way to characterize the simplicity—or complexity—of a sequence: we can consider a sequence more complex if the typical number of mutations it takes to come up with a rule to generate the sequence is larger. And we can define this number of mutations to be what we can call the “mutational complexity” of a sequence.
There are lots of details in tightening up this definition. But in some sense what we’re saying is that we can characterize the complexity of a sequence by how hard it is for adaptive evolution to get it generated.
To get more quantitative we have to address the issue that if we run adaptive evolution multiple times, it’ll generally take different numbers of steps to be able to get a particular sequence generated, or, say, to get to the point where there are fewer than m “errors” in the generated sequence. And, sometimes, by the way, a particular run of adaptive evolution might “get stuck” and never be able to generate a particular sequence—at least (as we’ll discuss below) with the kind of rules and single point mutations we’re using here.
But we can still compute the probability—across many runs of adaptive evolution—to have reached a specified sequence within m errors after a certain number of steps. And this shows how that probability builds up for the sequences we saw above:

And we immediately see more quantitatively that some sequences are faster and easier to reach than others.
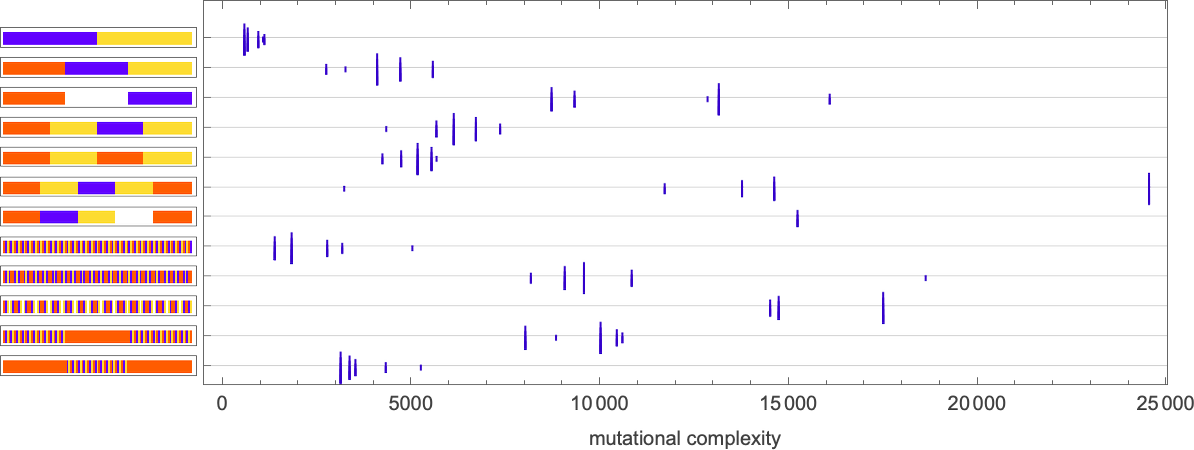
We can go even further by computing in each case the median number of adaptive steps needed to get “within m errors” of each sequence:

Picking a certain “desired fidelity” (say allowing a maximum of 20 errors) we then get at least one estimate of mutational complexity for our sequences:

Needless to say, these kinds of numerical measures are at best a very coarse way to characterize the difficulty of being able to generate a given sequence through rules produced by adaptive evolution. And, for example, instead of just looking at the probability to reach a given “fidelity” we could be looking at all sorts of distributions and correlations. But in developing our intuition about the rulial ensemble it’s useful to see how we can derive even an admittedly coarse specific numerical measure of the “difficulty of reaching a sequence” through adaptive evolution.
We’ve seen above that some sequences are easier to reach by adaptive evolution than others. But can any sequence we might look for actually be found at all? In other words—regardless of whether adaptive evolution can find it—is there in fact any cellular automaton rule at all (say a 4-color one) that successfully generates any given sequence?
It’s easy to see that in the end there must be sequences that can’t be generated in this way. There are 443 possible 4-color cellular automaton rules. But even though that’s a large number, the number of possible 4-color length-101 sequences is still much larger: 4101 ≈ 1061. So that means it’s inevitable that some of these sequences will not appear as the output from any 4-color cellular automaton rule (run from a single-cell initial condition for 50 steps). (We can think of such sequences as having too high an “algorithmic complexity” to be generated from a “program” as short as a 4-color cellular automaton rule.)
But what about sequences that are “simple” with respect to our qualitative criteria above? Whenever we succeeded above in finding them by adaptive evolution then we obviously know they can be generated. But in general this is a quintessential computationally irreducible question—so that in effect the only way to know for sure whether there’s any rule that can generate a particular sequence is just to explicitly search through all ≈ 1038 possible rules.
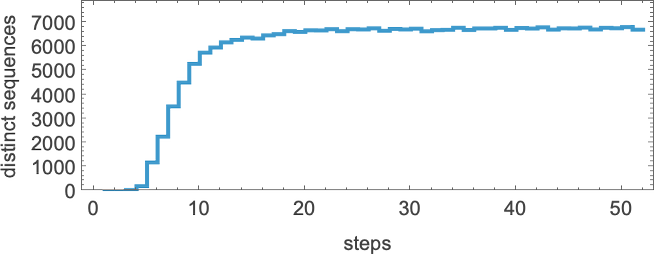
We can get some intuition, however, by looking at much simpler cases. Consider, for example, the 128 (quiescent) “elementary” cellular automata (with k = 2, r =1):

The number of distinct sequences they can generate after t steps quickly stabilizes (the maximum is 32)
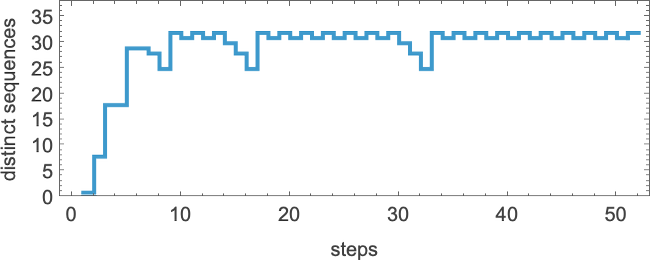
but this is soon much smaller than the total number of possible sequences of the same length (
So what are the sequences that get “left out” by cellular automata? Already by step 2 a quiescent elementary cellular automaton can only produce 14 of the 32 possible sequences—with sequences such as ![]() and
and ![]() being among those excluded. One might think that one would be able to characterize excluded sequences by saying that certain fixed blocks of cells could not occur at any step in any rule. And indeed that happens for the r = 1/2 rules. But for the quiescent elementary cellular automata—with r = 1—it seems as if every block of any given size will eventually occur, presumably courtesy of the likes of rule 30.
being among those excluded. One might think that one would be able to characterize excluded sequences by saying that certain fixed blocks of cells could not occur at any step in any rule. And indeed that happens for the r = 1/2 rules. But for the quiescent elementary cellular automata—with r = 1—it seems as if every block of any given size will eventually occur, presumably courtesy of the likes of rule 30.
What about, say, periodic sequences? Here are some examples that no quiescent elementary cellular automaton can generate:

And, yes, these are, by most standards, quite “simple” sequences. But they just happen not to be “simple” for elementary cellular automata. And indeed we can expect that there will be plenty of such “coincidentally unreachable” but “seemingly simple” sequences even for our 4-color rules. But we can also expect that even if we can’t precisely reach some objective sequence, we’ll still be able to get to a sequence that is close. (The minimum “error” is, for example, 4 cells out of 15 for the first sequence above, and 2 for the last sequence).
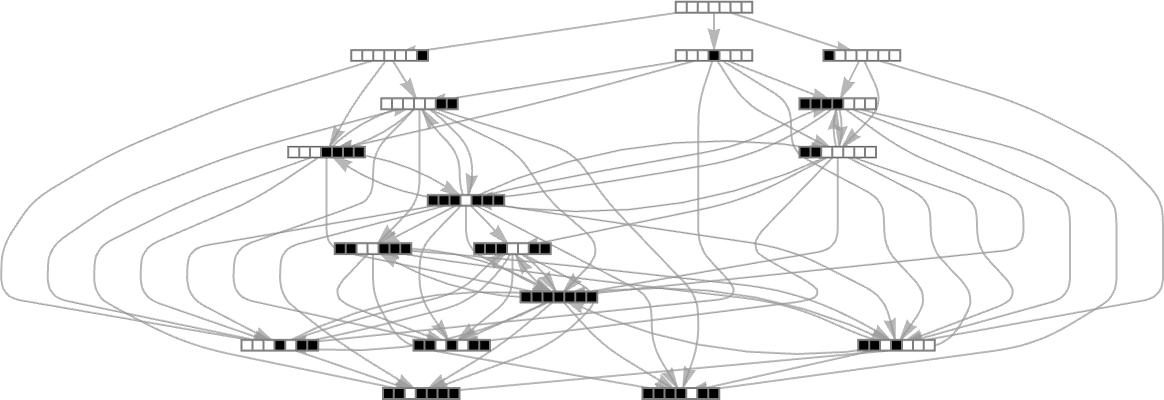
But there still remains the question of whether adaptive evolution will be able to find such sequences. For the very simple case of quiescent elementary cellular automata we can readily map out the complete multiway graph of all possible mutations between rules. Here’s what we get if we run all possible rules for 3 steps, then show possible outcomes as nodes, and possible mutations between rules as edges (the edges are undirected, because every mutation can go either way):

That this graph has only 18 nodes reflects the fact that quiescent elementary cellular automata can produce only 18 of the 128 possible length-7 sequences. But even within these 18 sequences there are ones that cannot be reached through the adaptive evolution process we are using.
For example, let’s say our goal is to generate the sequence ![]() (or, rather, to find a rule that will do so). If we start from the null rule—which generates
(or, rather, to find a rule that will do so). If we start from the null rule—which generates ![]() —then our adaptive evolution process defines a foliated version of the multiway graph above:
—then our adaptive evolution process defines a foliated version of the multiway graph above:
Starting from ![]() some paths (i.e. sequences of mutations) successfully reach
some paths (i.e. sequences of mutations) successfully reach ![]() . But this only happens about 25% of the time. The rest of the time the adaptive process gets stuck at
. But this only happens about 25% of the time. The rest of the time the adaptive process gets stuck at ![]() or
or ![]() and never reaches
and never reaches ![]() :
:
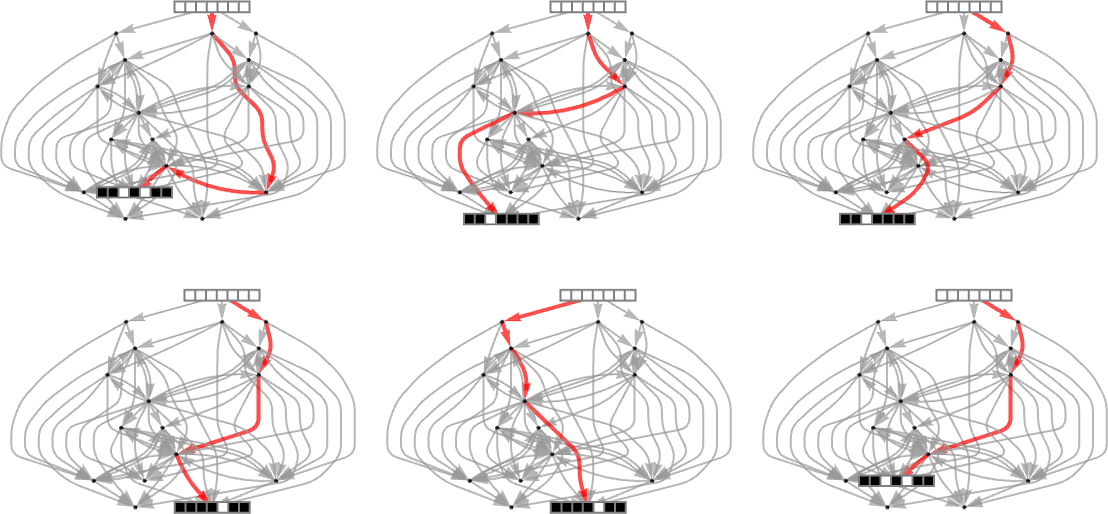
So what happens if we look at larger cellular automaton rule spaces? In such cases we can’t expect to trace the full multiway graph of possible mutations. And if we pick a sequence at random as our target, then for a long sequence the overwhelming probability is that it won’t be reachable at all by any cellular automaton with a rule of a given type. But if we start from a rule—say picked at random—and use its output as our target, then this guarantees that there’s at least one rule that produces this sequence. And then we can ask how difficult it is for adaptive evolution to find a rule that works (most likely not the original one).
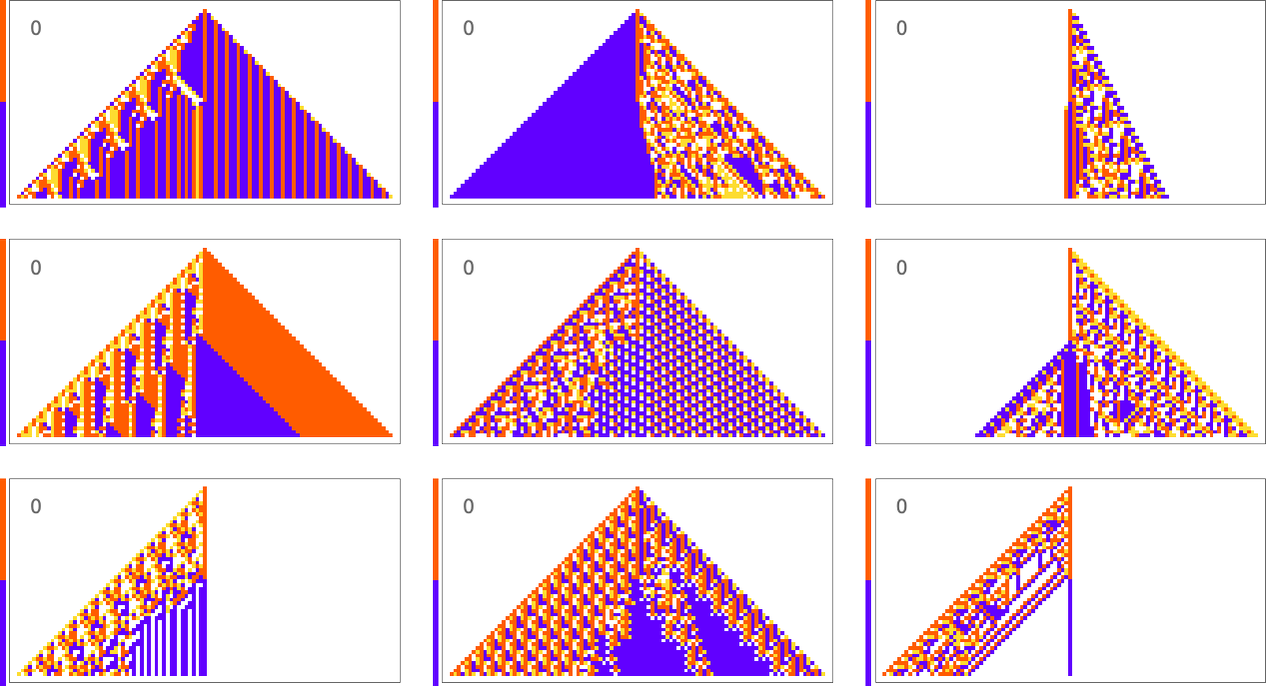
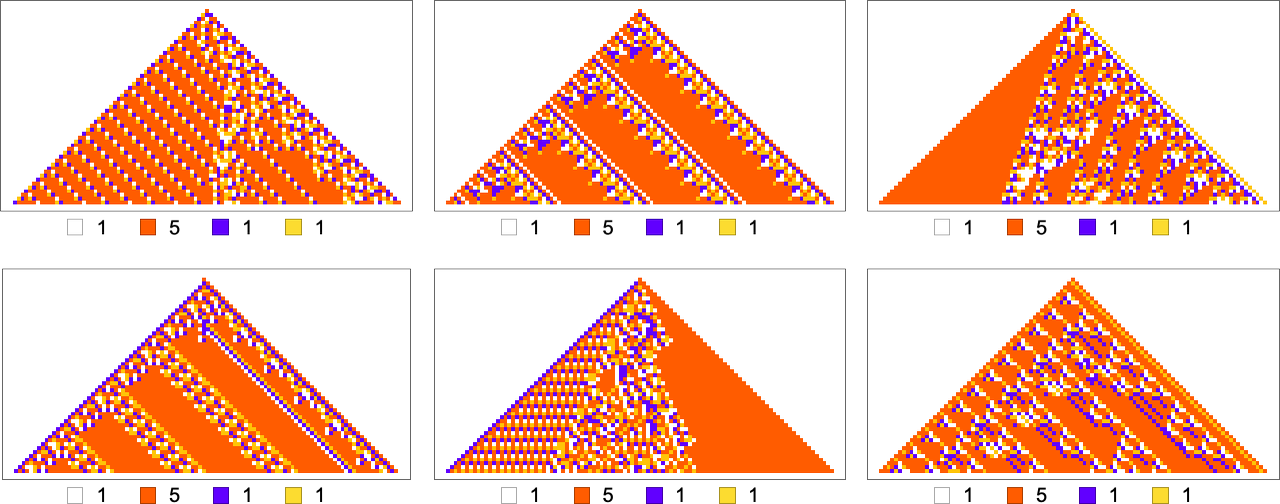
Here are some examples—with the original rule on the left, and the best results found from 10,000 steps of adaptive evolution on the right:
What we see is fairly clear: when the pattern generated by the original rule looks simple, adaptive evolution can readily find rules that successfully produce the same output, albeit sometimes in quite different ways. But when the pattern generated by the original rule is more complicated, adaptive evolution typically won’t be able to find a rule that exactly reproduces its output. And so, for examples, in the cases shown here many errors remain even in the “best results” after 10,000 steps of adaptive evolution.
Ultimately this not surprising. When we pick a cellular automaton rule at random, it’ll often show computational irreducibility. And in a sense all we’re seeing here is that adaptive evolution can’t “break” computational irreducibility. Or, put another way, computationally irreducible processes generate mutational complexity.
In everything we’ve done so far we’ve been considering a particular type of “goal”: to have a cellular automaton produce a specified arrangement of cells after a certain number of steps. But what about other types of goals? We’ll look at several here. The general features of what will happen with them follow what we’ve already seen, but each will show some new effects and will provide some new perspectives.
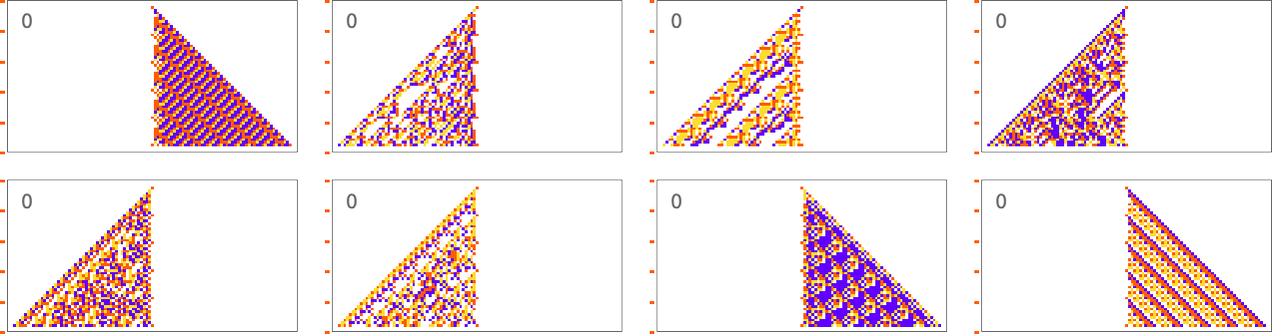
As a first example, let’s consider trying to match not the horizontal arrangement of cells, but the vertical one—in particular the sequence of colors in the center column of the cellular automaton pattern. Here’s what we get with the goal of having a block of red cells followed by an equal block of blue:
The results are quite diverse and “creative”. But it’s notable that in all cases there’s definite “mechanism” to be seen “right around the center column”. There’s all sorts of complexity away from the center column, but it’s sufficiently “contained” that the center column itself can achieve its “simple goal”.
Things are similar if we ask to get three blocks of color rather than two—though this goal turns out to be somewhat more difficult to achieve:
It’s also possible to get ![]() :
:

And in general the difficulty of getting a particular vertical sequence of blocks tends to track the difficulty of getting the corresponding horizontal sequence of blocks. Or, in other words, the pattern of mutational complexity seems to be similar for sequences associated with horizontal and vertical goals.
This also seems to be true for periodic sequences. Alternating colors are easy to achieve, with many “tricks” being possible in this case:
A sequence with period 5 is pretty much the same story:

When the period gets more comparable to the number of cellular automaton steps that we’re sampling it for, the “solutions” get wilder:
And some of them are quite “fragile”, and don’t “generalize” beyond the original number of steps for which they were adapted:
The types of goals we’ve considered so far have all involved trying to get exact matches to specified sequences. But what if we just ask for an average result? For example, what if we ask for all 4 colors to occur with equal frequency in our output, but allow them to be arranged in any way? With the same adaptive evolution setup as before we rather quickly find “solutions” (where because we’re running for 50 steps and getting patterns of width 101, we’re always “off by at least 1” relative to the exact 25:25:25:25 result):
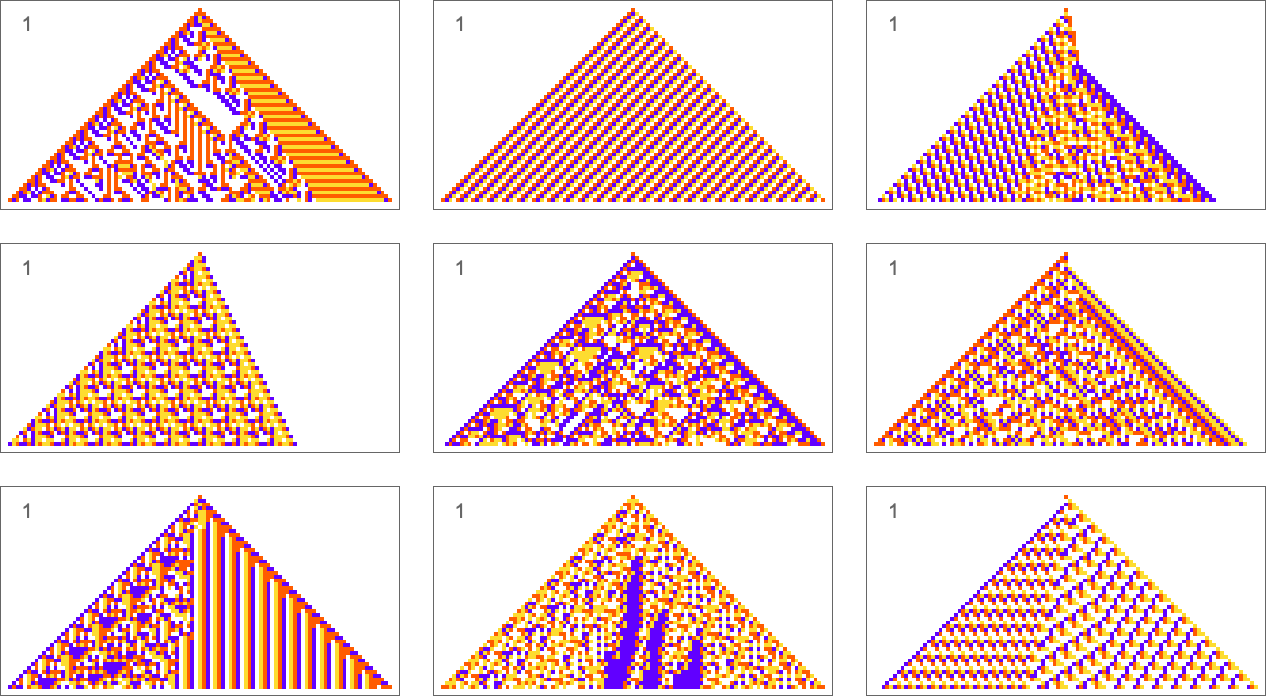
A few of these solutions seem to have “figured out a mechanism” to get all colors equally. But others seem like they just “happen to work”. And indeed, taking the first three cases here, this shows the relative numbers of cells of different colors obtained at successive steps in running the cellular automaton:
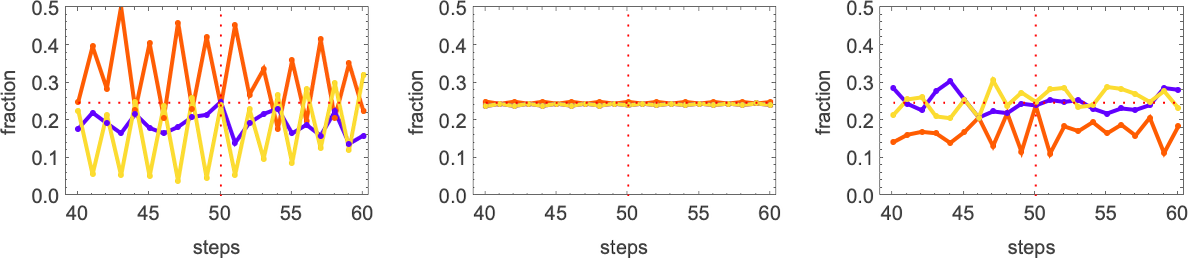
The pattern that looks simple consistently has equal numbers of each color at every step. The others just “happen to hit equality” after running for exactly 50 steps, but on either side don’t achieve equality.
And, actually, it turns out that all these solutions are in some sense quite fragile. Change the color of just one cell and one typically gets an expanding region of change—that takes the output far from color equality:
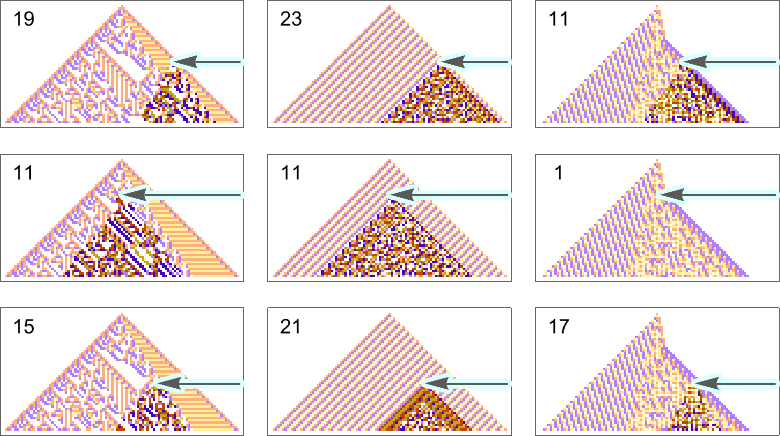
So how can we get rules that more robustly achieve our color equality objective? One approach is to force the adaptive evolution to “take account of possible perturbations” by applying a few perturbations at every adaptive evolution step, and keeping a particular mutation only if neither it, nor any of its perturbed versions, has lower fitness than before.
Here’s an example of one particular sequence of successive rules obtained in this way:

And now if we apply perturbations to the final result, it doesn’t change much:

It’s notable that this robust solution looks simple. And indeed that’s common, with a few other examples of robust, exact solutions being:
In effect it seems that requiring a robust, exact solution “forces out” computational irreducibility, leaving only readily reducible patterns. If we relax the constraint of being an exact solution even a little, though, more complex behavior quickly creeps in:
We’ve just looked at trying to achieve particular frequencies of colors in the “output” of a cellular automaton (after running for 50 steps). But what if we try to achieve certain frequencies of colors throughout the pattern produced by the cellular automaton?
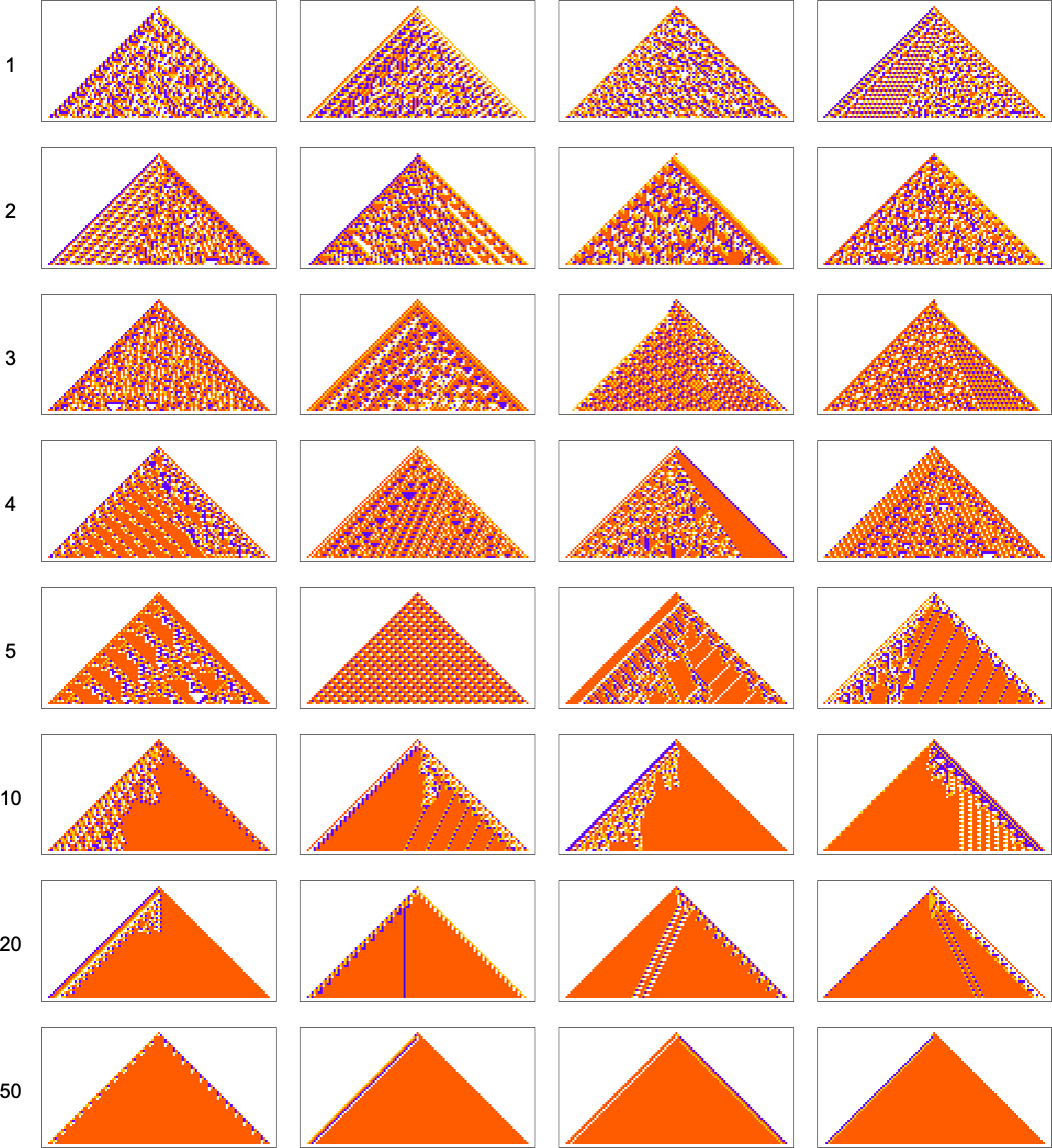
For example, let’s say that our goal is to have color frequencies in the ratios: ![]() . Adaptive evolution fairly easily finds good “solutions” for this:
. Adaptive evolution fairly easily finds good “solutions” for this:
And in fact it does so for any “relative red level”:
But if we plot the median number of adaptive evolution steps needed to achieve these results (i.e. our approximation to mutational complexity) we see that there’s a systematic increase with “red level”:
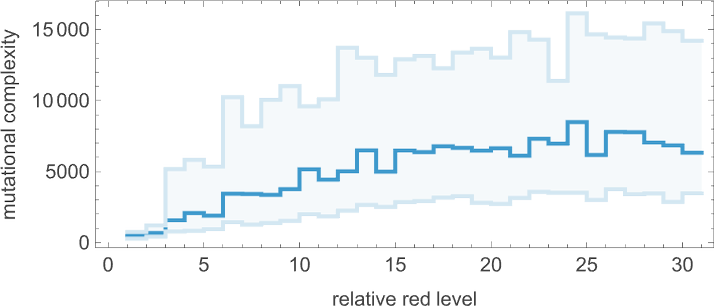
In effect, the higher the red level the “more stringent” the constraints we’re trying to satisfy are—and the more steps of adaptive evolution it takes to do that. But looking at the actual patterns obtained at different red levels, we also see something else: that as the constraints get more stringent, the pattern seems to have computational irreducibility progressively “squeezed out” of them—leaving behavior that seems more and more mechanoidal.
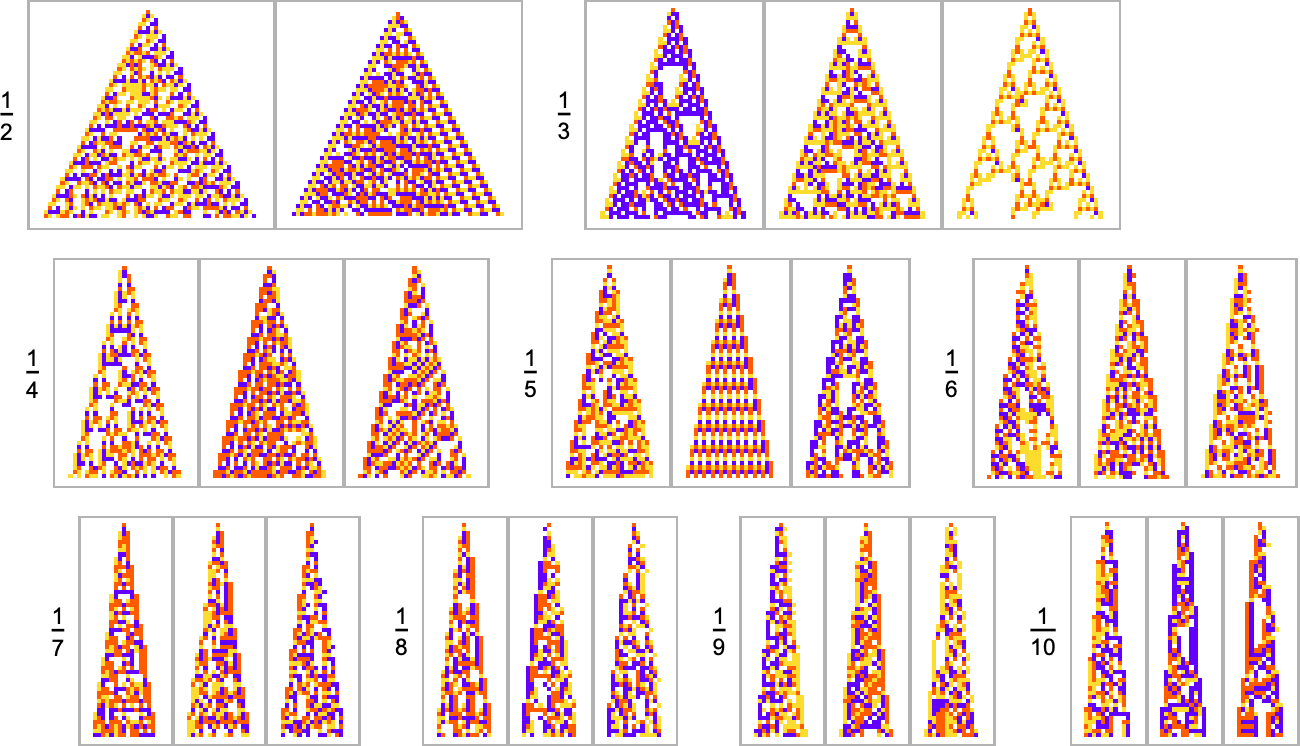
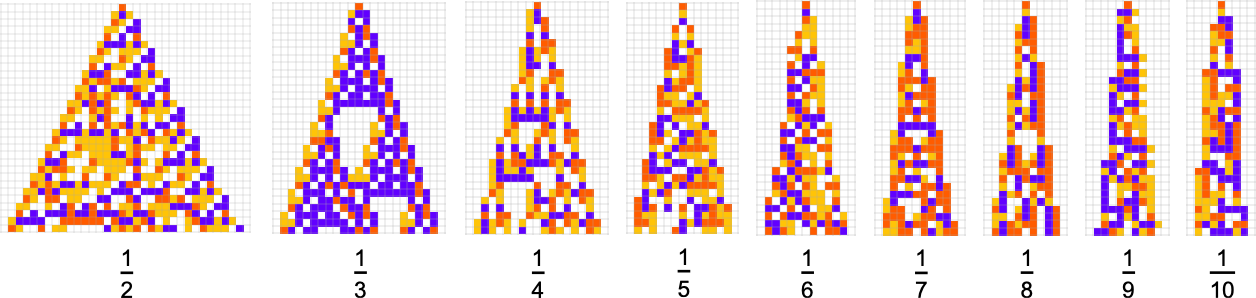
As another example along the same lines, consider goals of the form ![]() . Here are results one gets varying the “white level”:
. Here are results one gets varying the “white level”:
We see two rather different approaches being taken to the “problem of having more white”. When the white level isn’t too large, the pattern just gets “airier”, with more white inside. But eventually the pattern tends to contract, “leaving room” for white outside.
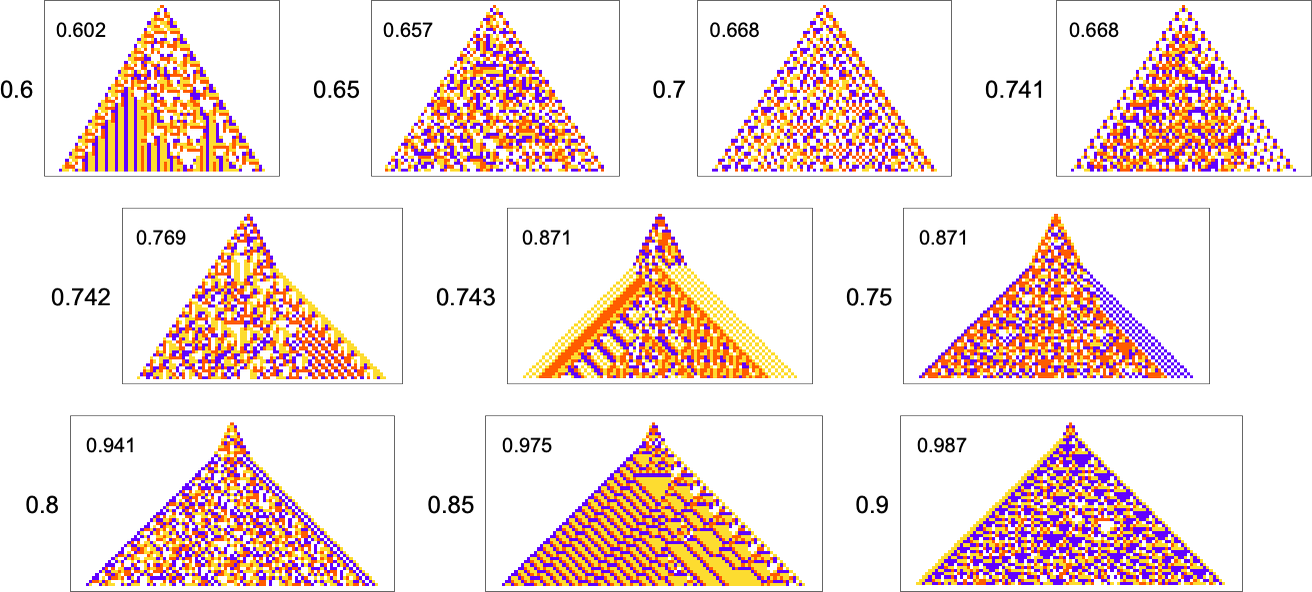
In most of what we’ve done so far, the overall “shapes” of our cellular automaton patterns have ended up always just being simple triangles that expand by one cell on each side at each step—though we just saw that with sufficiently stringent constraints on colors they’re forced to be different shapes. But what if our actual goal is to achieve a certain shape? For example, let’s say we try to get triangular patterns that grow at a particular rate on each side.
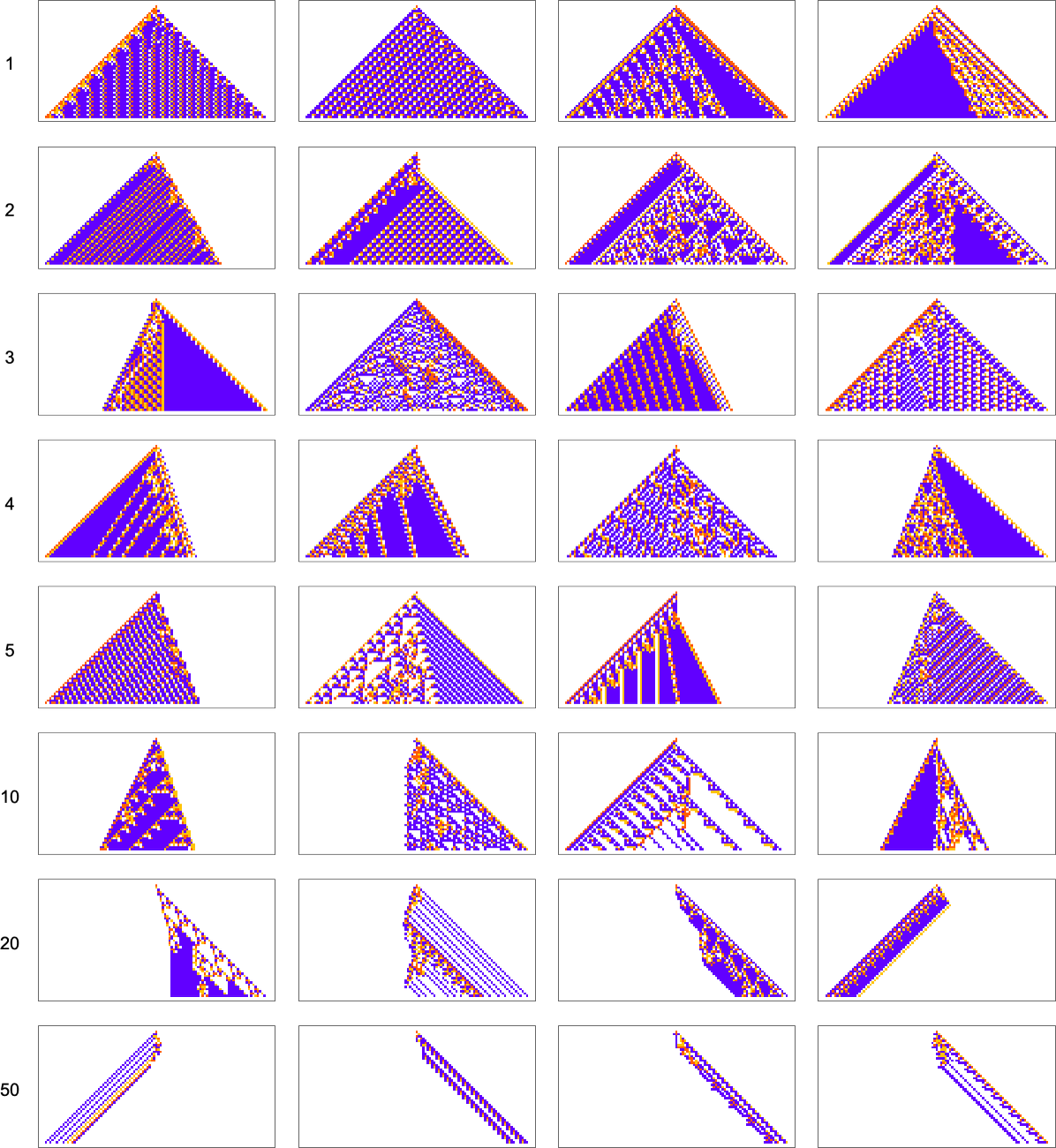
Here are some results for growth rates of the form 1/n (i.e. growing by an average of 1 cell every n steps):
This is the sequence of adaptive evolution steps that led to the first example of growth rate ![]()
and this is the corresponding sequence for growth rate ![]() :
:

And although the interiors of most of the final patterns here are complicated, their outer boundaries tend to be simple—at least for small n—and in a sense “very mechanically” generate the exact target growth rate:
For larger n, things get more complicated—and adaptive evolution doesn’t typically “find an exact solution”. And if we run our “solutions” longer we see that—particularly for larger n—they often don’t “generalize” very well, and soon start deviating from their target growth rates:
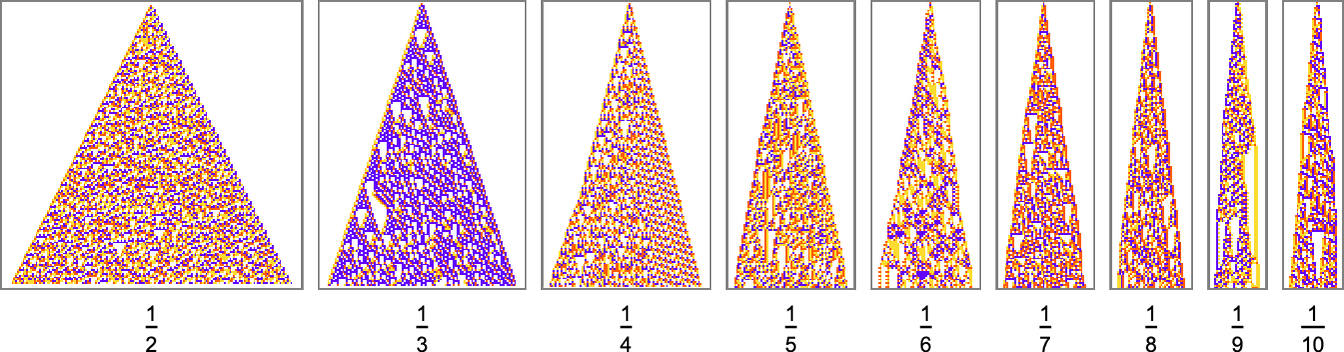
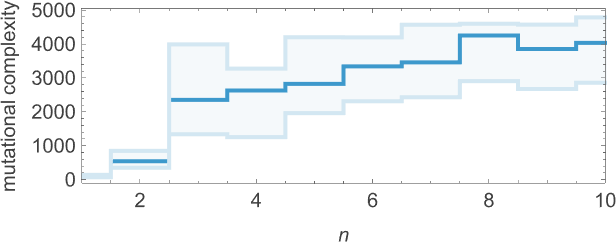
As we increase n we typically see that more steps of adaptive evolution are needed to achieve our goal, reflecting the idea that “larger n growth” has more mutational complexity:
For rational growth rates like ![]() fairly simple exact solutions are possible. But for irrational growth rates, that’s no longer true. Still, it turns out that adaptive evolution is in a sense strong enough—and our cellular automaton rule space is large enough—that good approximations even to irrational growth rates can often be reached:
fairly simple exact solutions are possible. But for irrational growth rates, that’s no longer true. Still, it turns out that adaptive evolution is in a sense strong enough—and our cellular automaton rule space is large enough—that good approximations even to irrational growth rates can often be reached:
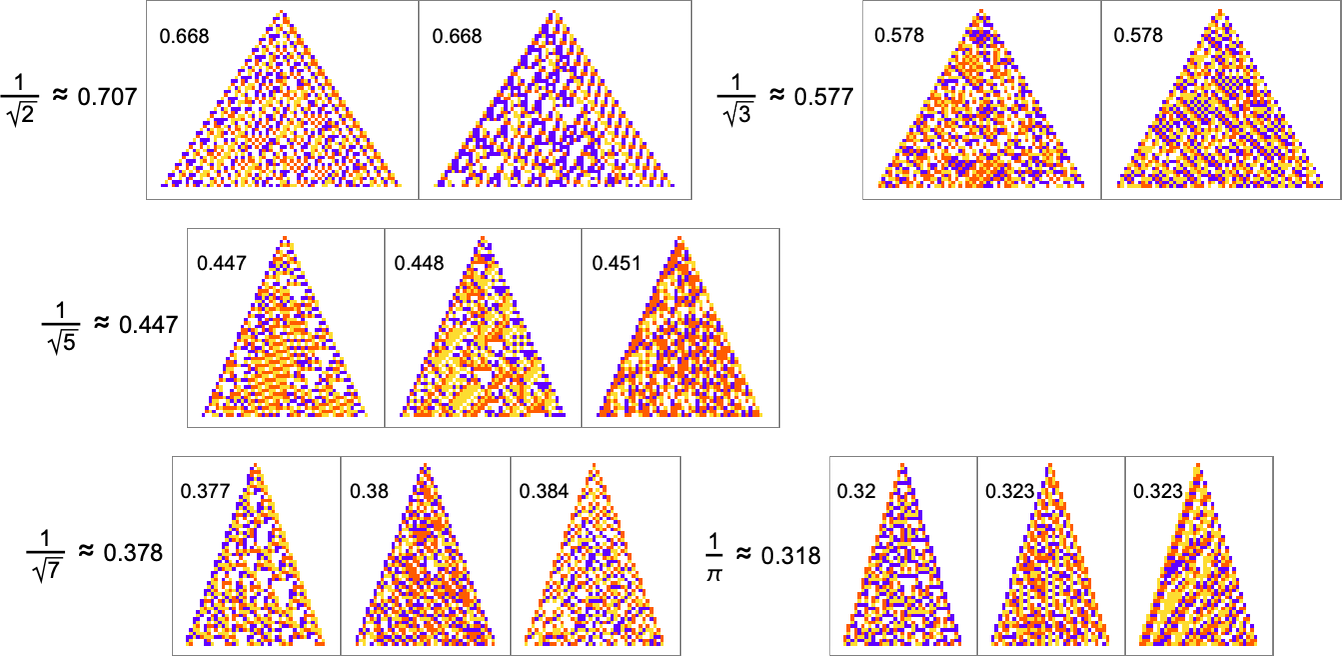
The “solutions” typically remain quite consistent when run longer:
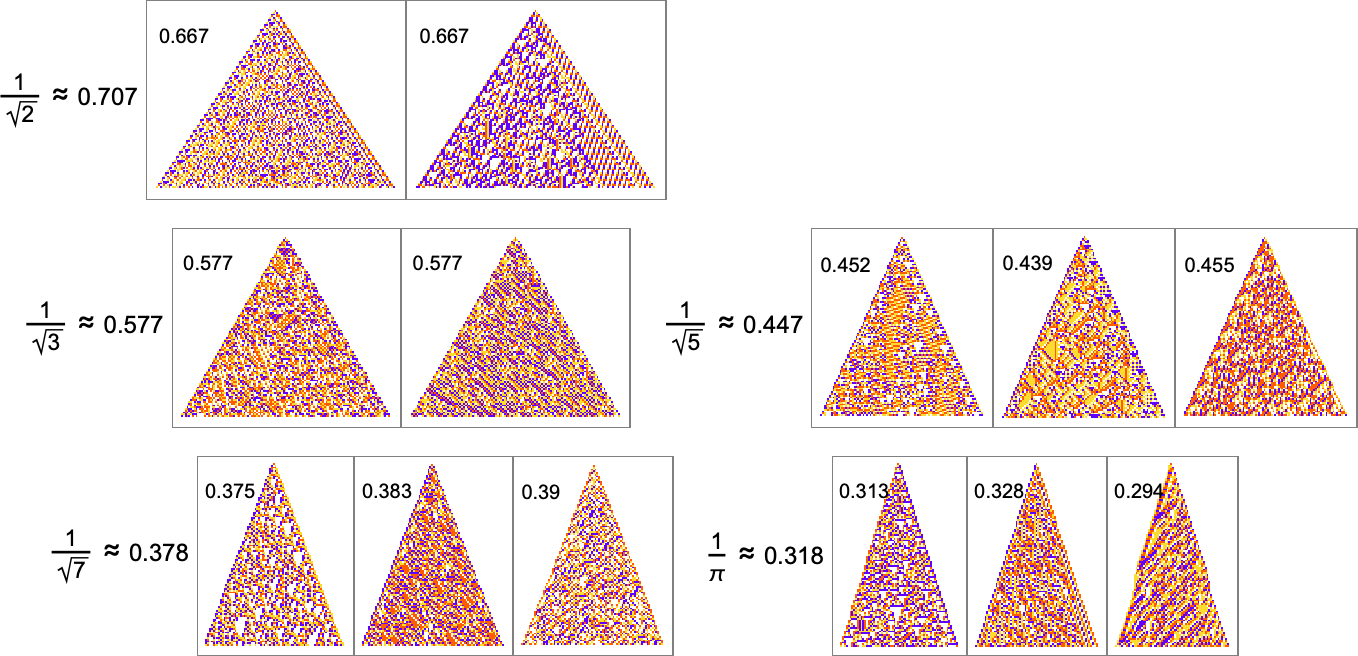
But there are still some notable limitations. For example, while a growth rate of exactly 1 is easy to achieve, growth rates close to 1 are in effect “structurally difficult”. For example, above about 0.741 adaptive evolution tends to “cheat”—adding a “hat” at the top of the pattern instead of actually producing a boundary with consistent slope:
What about other shapes as goals? Here’s what happens with diamond shapes of difficult widths:
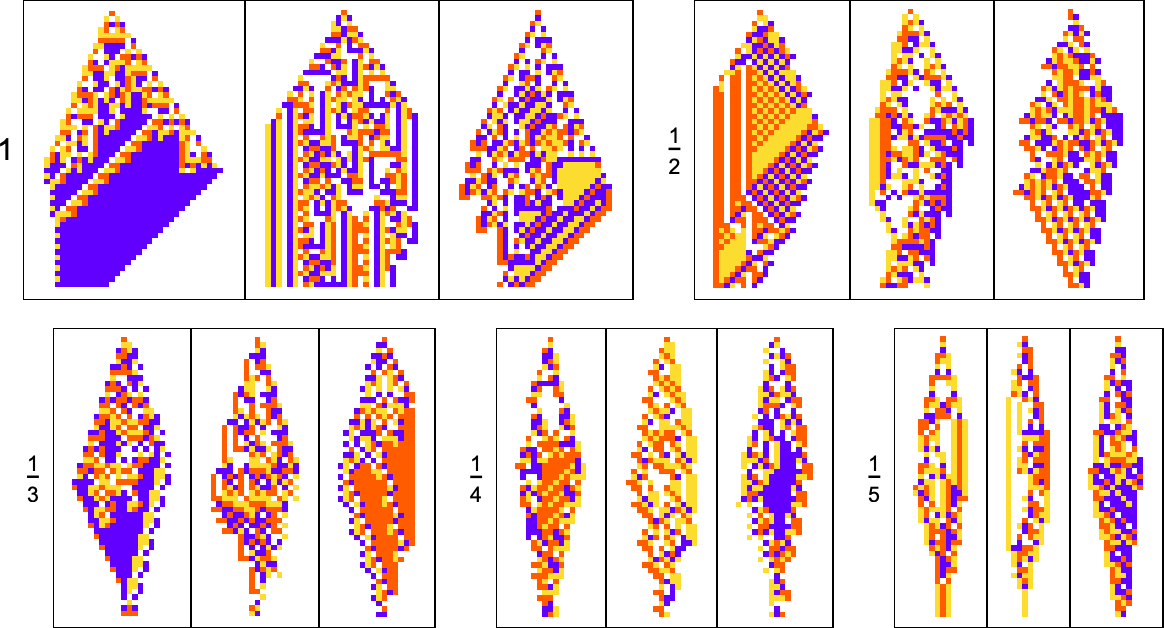
Adaptive evolution is quite constrained by what’s structurally possible in a cellular automaton of this type—and the results are not particularly good. And indeed if one attempts to “generalize” them, it’s clear none of them really “have the idea” of a diamond shape:

In the examples we’ve discussed so far, we’ve focused on what cellular automata do over the course of a fixed number of steps—not worrying about what they might do later. But another goal we might have—which in fact I have discussed at length elsewhere—is just to have our cellular automata produce patterns that go for a certain number of steps and then die out. So, for example, we can use adaptive evolution to find cellular automata whose patterns live for exactly 50 steps, and then die out:
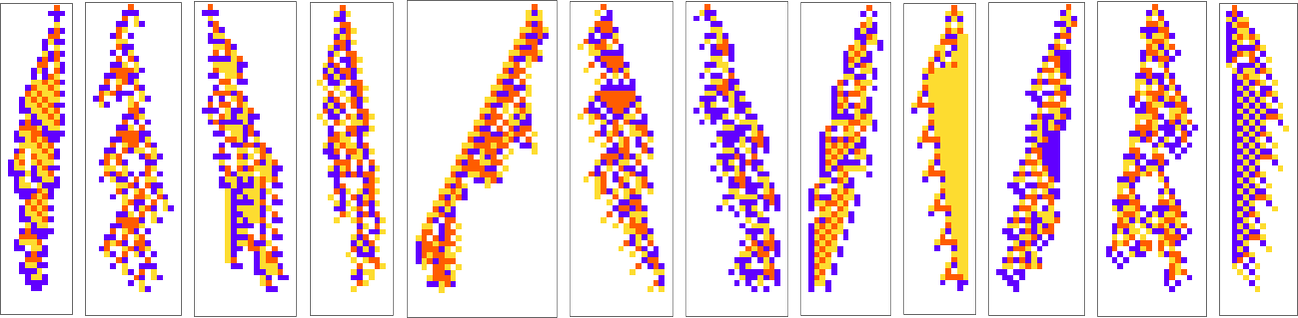
Just like in our other examples, adaptive evolution finds all sorts of diverse and “interesting” solutions to the problem of living for exactly 50 steps. Some (like the last one and the yellow one) have a certain level of “obvious mechanism” to them. But most of them seem to “just work” for no “obvious reason”. Presumably the constraint of living for 50 steps in some sense just isn’t stringent enough to “squeeze out” computational irreducibility—so there is still plenty of computational irreducibility in these results.
What about mutational complexity? Approximating this, as before, by the median of the number of adaptive evolution steps—and sampling a few hundred cases for each lifetime goal (and plotting the quartiles as well as the median)—we see a systematic increase of mutational complexity as we increase the lifetime goal:
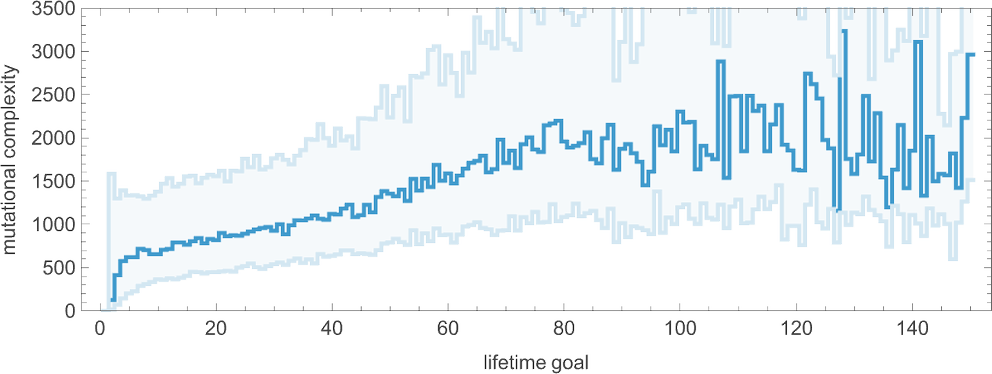
In effect this shows us that if we increase the lifetime goal, it becomes more and more difficult for adaptive evolution to reach that goal. (And, as we’ve discussed elsewhere, if we go far enough, we’ll ultimately reach the edge of what’s even in principle possible with, say, the particular type of 4-color cellular automata we’re using here.)
All the objectives we’ve discussed so far have the feature that they are in a sense explicit and fixed: we define what we want (e.g. a cellular automaton pattern that lives for exactly 50 steps) and then we use adaptive evolution to try to get it. But looking at something like lifetime suggests another possibility. Instead of our objective being fixed, our objective can instead be open ended. And so, for example, we might ask not for a specific lifetime, but to get the largest lifetime we can.
I’ve discussed this case at some length elsewhere. But how does it relate to the concept of the rulial ensemble that we’re studying here? When we have rules that are found by adaptive evolution with fixed constraints we end up with something that can be thought of as roughly analogous to things like the canonical (“specified temperature”) ensemble of traditional statistical mechanics. But if instead we look at the “winners” of open-ended adaptive evolution then what we have is more like a collection of extreme value than something we can view as typical of the “bulk of an ensemble”.
We’ve just looked at the goal of having patterns that survive for a certain number of steps. Another goal we can consider is having patterns that periodically repeat after a certain number of steps. (We can think of this as an extremely idealized analog of having multiple generations of a biological organism.)
Here are examples of rules found by adaptive evolution that lead to patterns which repeat after exactly 50 steps:
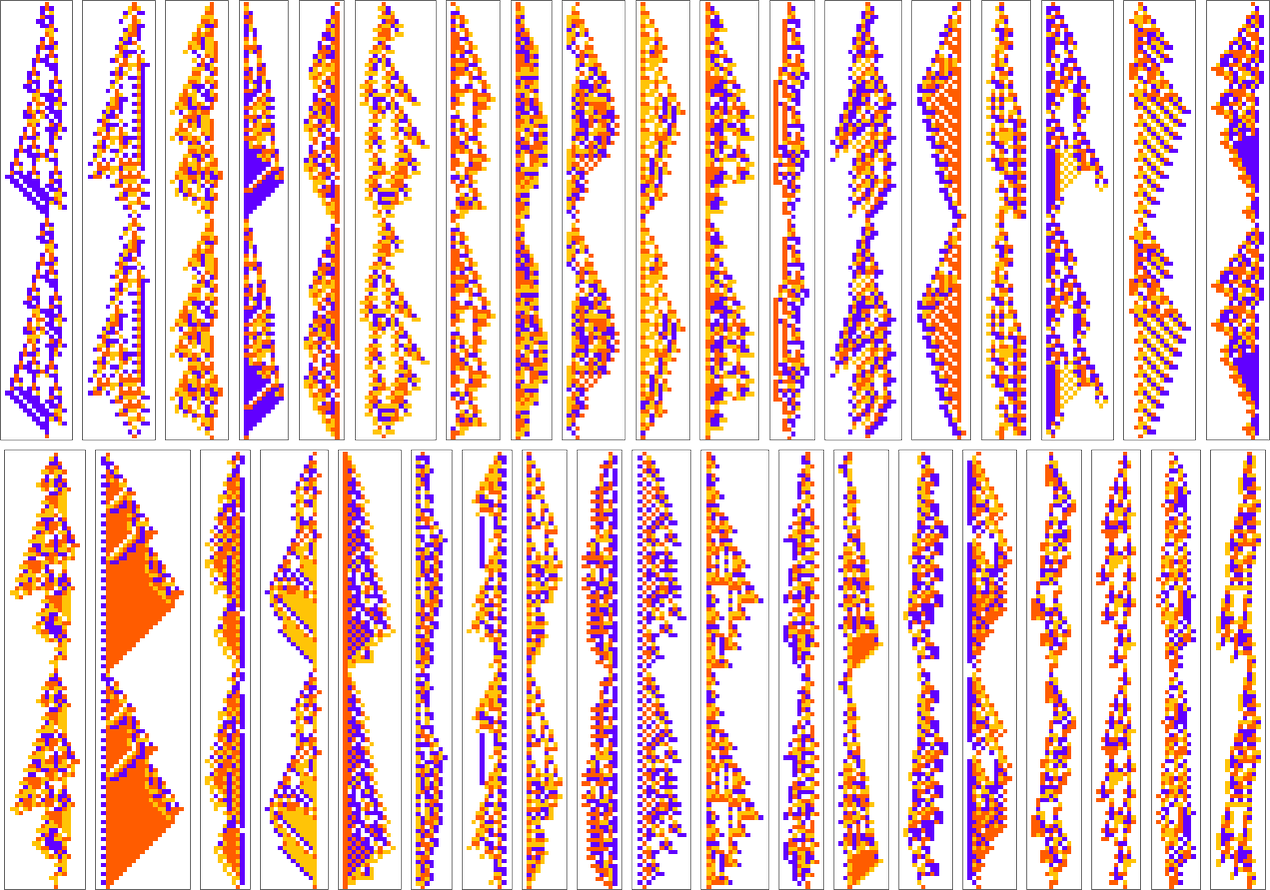
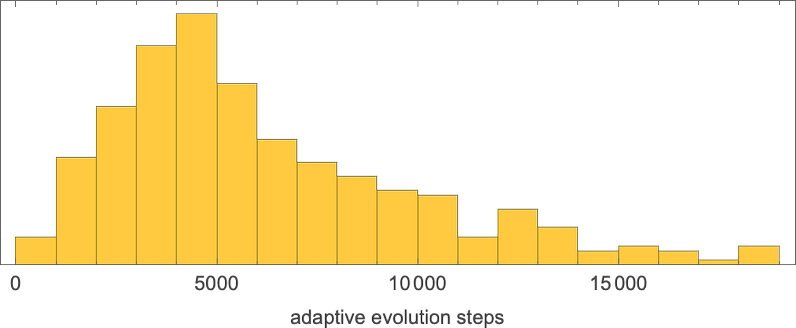
As usual, there’s a distribution in the number of steps of adaptive evolution required to achieve these results:
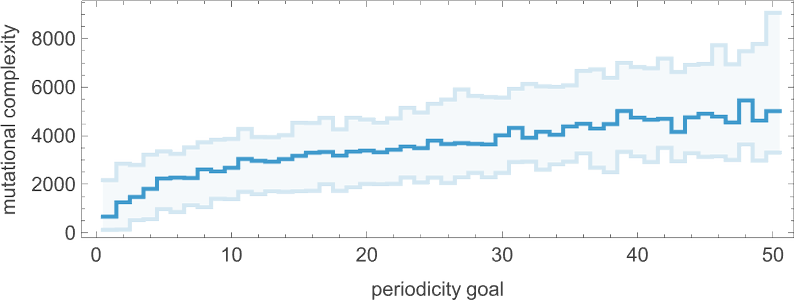
Looking at the median of the analogous distributions for different possible periods, we can get an estimate of the mutational complexity of different periods—which seems to increase somewhat uniformly with period:
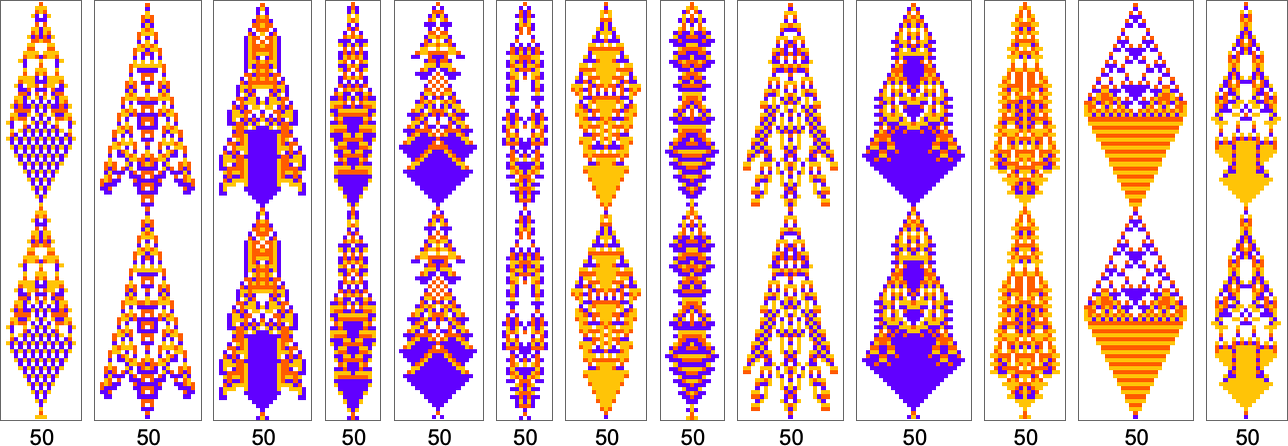
By the way, it’s also possible to restrict our adaptive evolution so that it samples only symmetric rules; here are a few examples of period-50 results found in this way:
In our discussion of periodicity so far, we’ve insisted on “periodicity from the start”—meaning that after each period the pattern we get has to return to the single-cell state we started from. But we can also consider periodicity that “develops after a transient”. Sometimes the transient is short; sometimes it’s much longer. Sometimes the periodic pattern starts from a small “seed”; sometimes its seed is quite large. Here are some examples of patterns found by adaptive evolution that have ultimate period 50:

By the way, in all these cases the periodic pattern seems like the “main event” of the cellular automaton evolution. But there are other cases where it seems more like a “residue” from other behavior—and indeed that “other behavior” can in principle go on for arbitrarily long before finally giving way to periodicity:

We’ve been talking so far about the objective of finding cellular automaton rules that yield patterns with specific periodicity. But just like for lifetime, we can also consider the “open-ended objective” of finding rules with the longest periods we can. And here are the best results found with a few runs of 10,000 steps of adaptive evolution (here we’re looking for periodicity without transients):
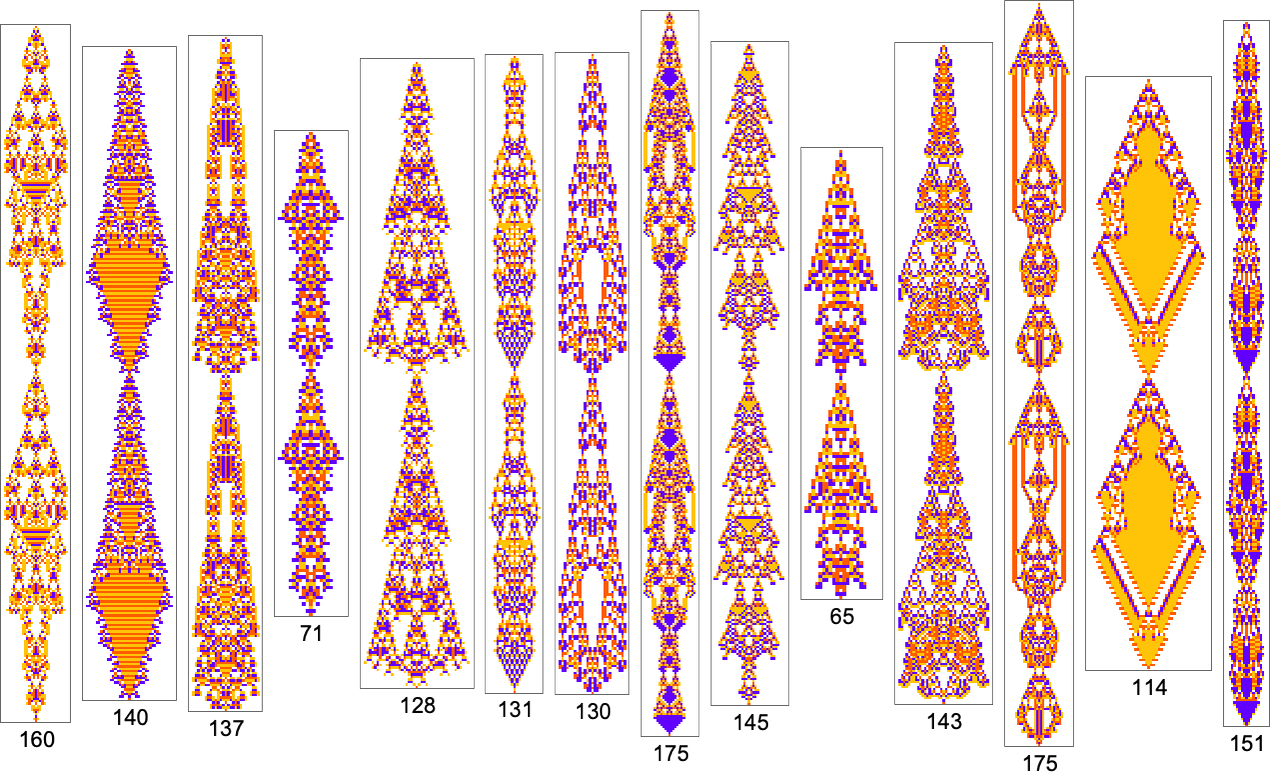
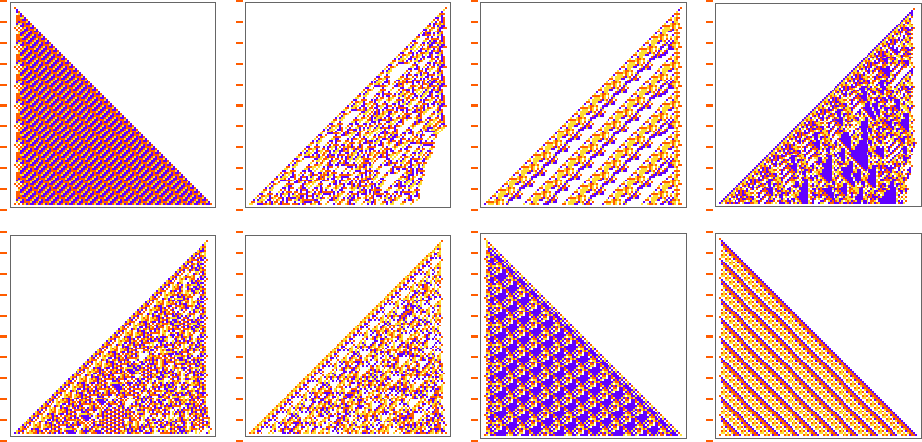
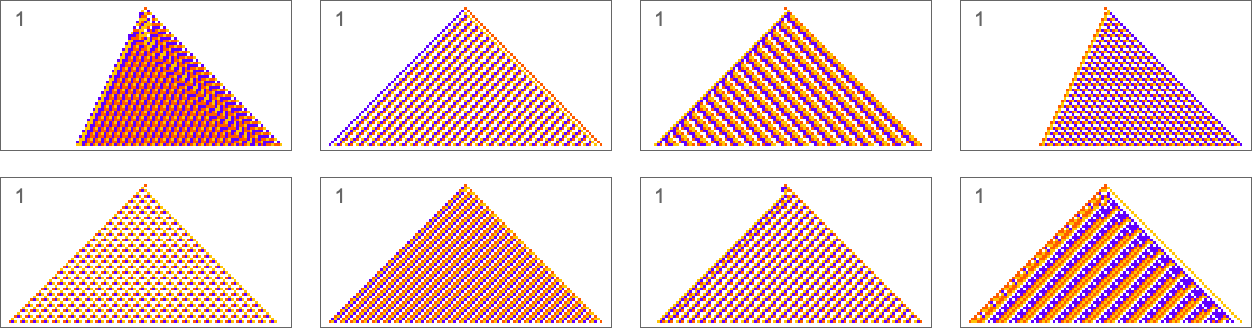
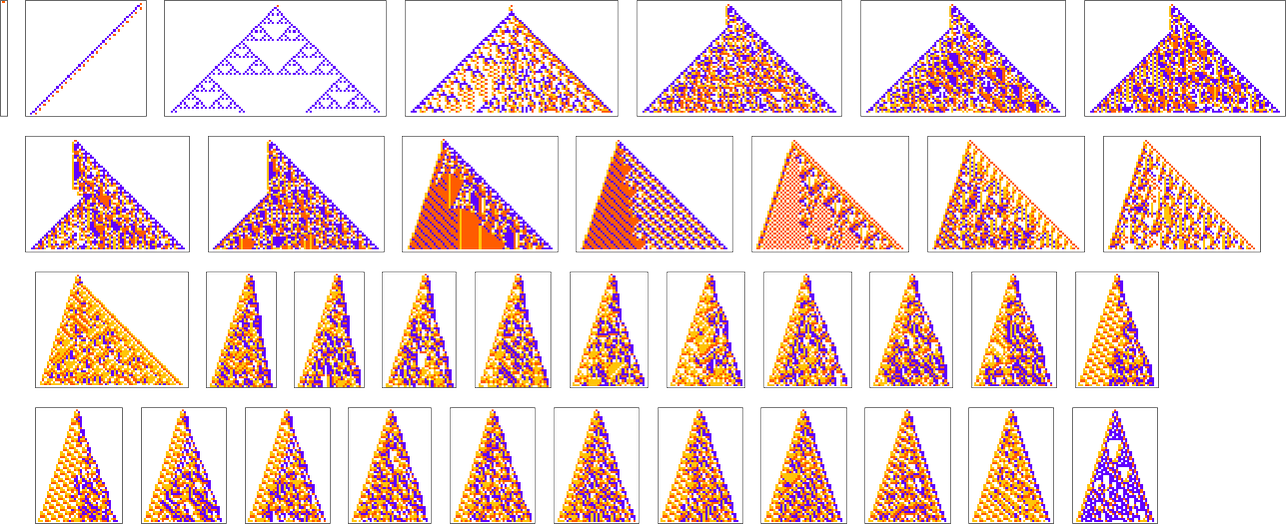
We’ve now seen lots of examples of cellular automata found by adaptive evolution. And a key question is: “what’s special about them?” If we look at cellular automata with rules chosen purely at random, here are typical examples of what we get:
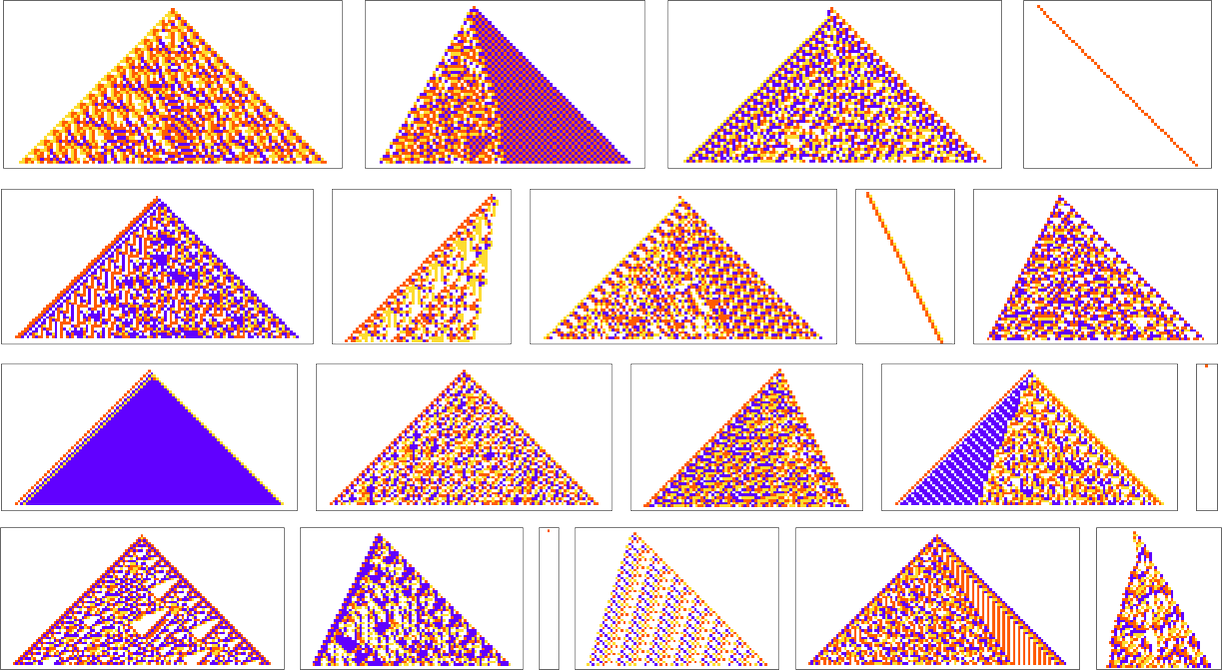
Some of these patterns are simple. But many are complicated and in fact look quite random—though often with regions or patches of regularity. But what’s striking is how visually different they look from what we’ve mostly seen above in cellular automata that were adaptively evolved “for a purpose”.
So how can we characterize—and ultimately measure—that difference? Our randomly picked cellular automata seem to show either almost total computational reducibility or “unchecked computational irreducibility” (albeit usually with regions or patches of computational reducibility). But cellular automata that were successfully “evolved for a purpose” tend to look different. They tend to show what we’re calling mechanoidal behavior: behavior in which there are identifiable “mechanism-like features”, albeit usually mixed in with at least some—typically highly contained—“sparks of computational irreducibility”.
At a visual level there are typically some clear characteristics to mechanoidal behavior. For example, there are usually repeated motifs that appear throughout a system. And there’s also usually a certain degree of modularity, with different parts of the system operating at least somewhat independently. And, yes, there’s no doubt a rich phenomenology of mechanoidal behavior to be studied (closely related to the study of class 4 behavior). But at a coarse and potentially more immediately quantitative level a key feature of mechanoidal behavior is that it involves a certain amount of regularity, and computational reducibility.
So how can one measure that? Whenever there’s regularity in a system it means there’s a way to summarize what the system does more succinctly than by just specifying every state of every element of the system. Or, in other words, there’s a way to compress our description of the system.
Perhaps, one might think, one could use modularity to do this compression, say by keeping only the modular parts of a system, and eliding away the “filler” in between—much like run-length encoding. But—like run-length encoding—the most obvious version of this runs into trouble when the “filler” consists, say, of alternating colors of cells. One can also think of using block-based encoding, or dictionary encoding, say leveraging repeated motifs that appear. But it’s an inevitable feature of computational irreducibility that in the end there can never be one universally best method of compression.
But as an example, let’s just use the Wolfram Language Compress function. (Using GZIP, BZIP2, etc. gives essentially identical results.) Feed in a cellular automaton pattern, and Compress will give us a (losslessly) compressed version of it. We can then use the length of this as a measure of what’s left over after we “compress out” the regularities in the pattern. Here’s a plot of the “compressed description length” (in “Compress output bytes”) for some of the patterns we’ve seen above:
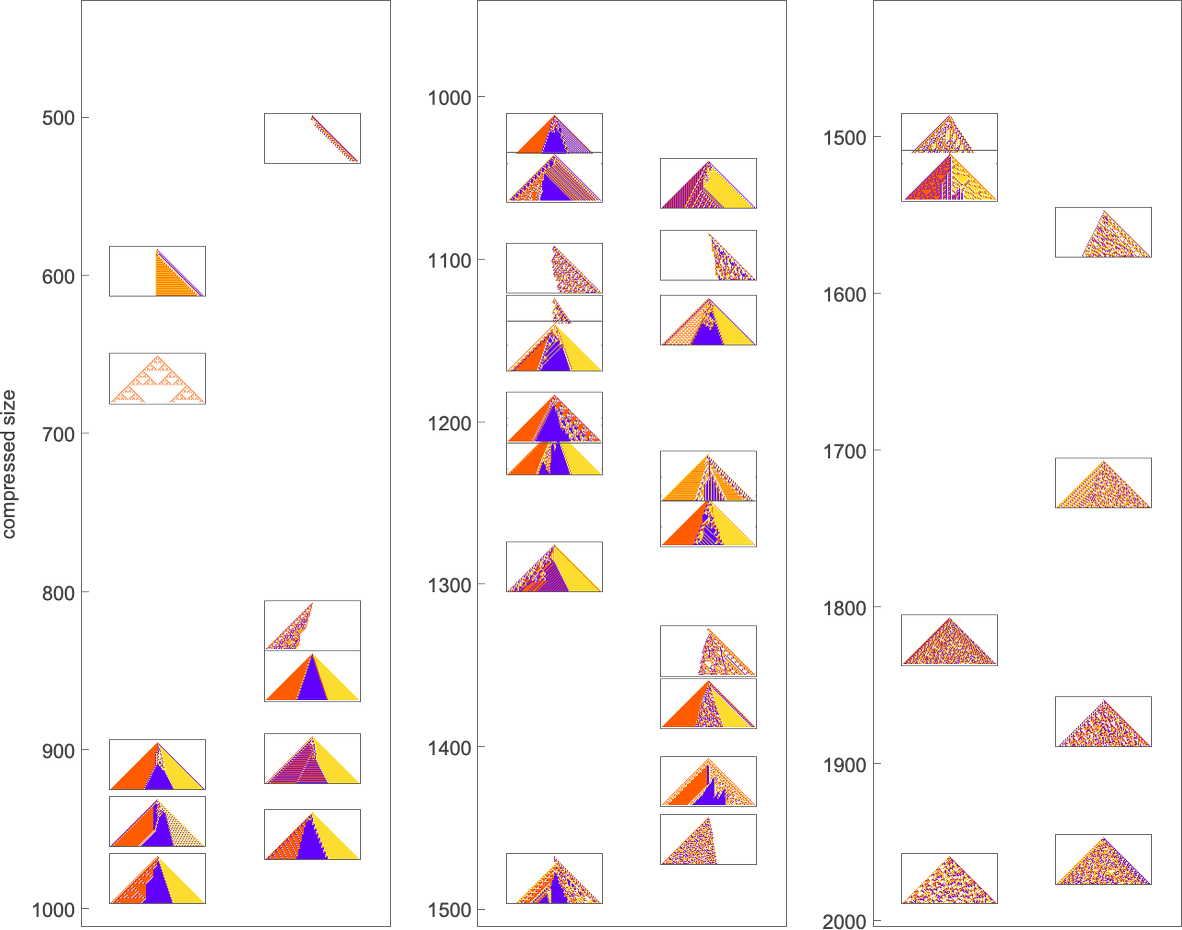
And what’s immediately striking is that the patterns “evolved for a purpose” tend to be in between patterns that come from randomly chosen rules.
(And, yes, the question of what’s compressed by what is a complicated, somewhat circular story. Compression is ultimately about making a model for things one wants to compress. And, for example, the appropriate model will change depending on what those things are. But for our purposes here, we’ll just use Compress—which is set up to do well at compressing “typical human-relevant content”.)
OK, so how does adaptive evolution relate to our “compressed size” measure? Here’s an example of the typical progression of an adaptive evolution process—in this case based on the goal of generating the ![]() sequence:
sequence:
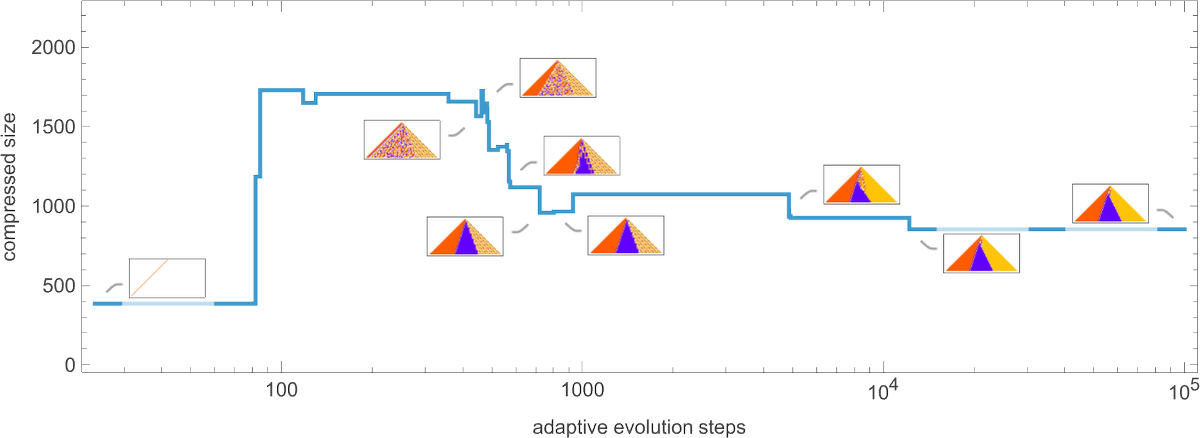
Given our way of starting with the null rule, everything is simple at the beginning—yielding a small compressed size. But soon the system starts developing computational irreducibility, and the compressed size goes up. Still, as the adaptive evolution proceeds, the computational irreducibility is progressively “squeezed out”—and the compressed size settles down to a smaller value.
The plot above is based on a particular (randomly chosen) sequence of mutations in the underlying rule. But if we look at the average from a large collection of mutation sequences we see very much the same thing:
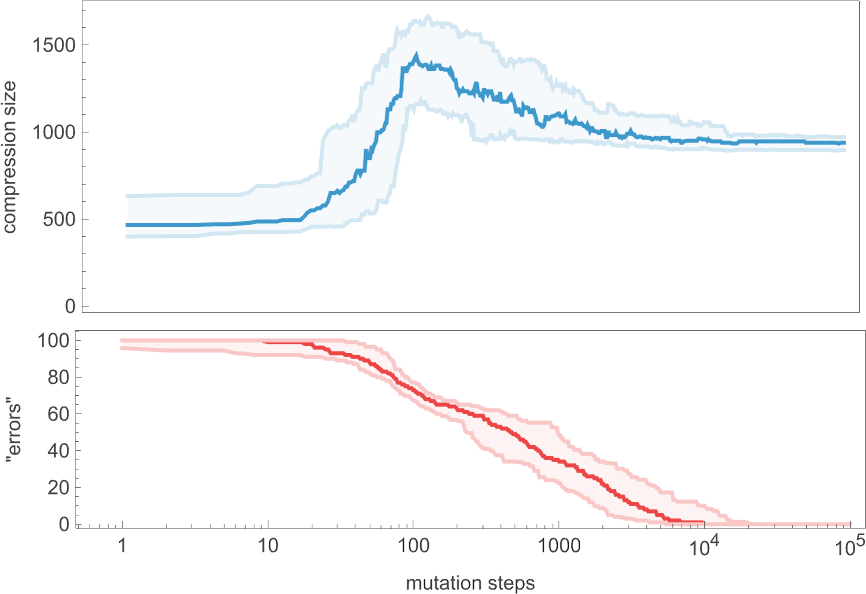
Even though the “error rate” on average goes down monotonically, the compressed size of our candidate patterns has a definite peak before settling to its final value. In effect, it seems that the system needs to “explore the computational universe” a bit before figuring out how to achieve its goal.
But how general is this? If we don’t insist on reaching zero error we get a curve of the same general shape, but slightly smoothed out (here for 20 or fewer errors):

What about for other target sequences? Here are results for all the target sequences we considered before (with the number of errors allowed in each case indicated):
In all cases we get final compressed sizes that are much smaller than those for all-but-very-simple randomly chosen rules—indicating that our adaptive evolution process has indeed generated regularity, and our compression method has successfully picked this up.
Looking at the overall shape of the curves we’ve generated here, there seems to be a general phenomenon in evidence: the process of adaptive evolution seems to pass through a “computationally irreducible period” before getting to its final mechanoidal state. Even as it gets progressively closer to its goal, the adaptive evolution process ends up still “playing the field” before homing in on its “final solution”. (And, yes, phenomena like this are seen both in the fossil record of life on Earth and in the development of engineering systems.)
We began by asking the question “what consequences does being ‘evolved for a purpose’ have on a system?” We’ve now seen many examples of different “purposes”, and how adaptive evolution can achieve them. The details are different in different cases. But we’ve seen that there are general features that occur very broadly. Perhaps most notable is that in systems that were “adaptively evolved for a purpose” one tends to see what we can call mechanoidal behavior: behavior in which there are “mechanism-like” elements.
Rules that are picked purely at random—in effect uniformly from rulial space—rarely show mechanoidal behavior. But in rules that have been adaptively evolved for a purpose mechanoidal behavior is the norm. And what we’ve found here is that this is true essentially regardless of what the specific purpose involved is.
We can think of rules that have been adaptively evolved for a purpose as forming what we can call a rulial ensemble: a subset of the space of all possible rules, concentrated by the process of adaptive evolution. And what we’ve seen here is that there are in effect generic features of the rulial ensemble—features that are generically seen in rules that have been adaptively evolved for a purpose.
Given a particular purpose (like “produce this specific sequence as output”) there are typically many ways it can be achieved. It could be that one can engineer a solution that shows a “human-recognizable mechanism” all the way through. It could be that it would be a “lump of computationally irreducible behavior” that somehow “just happens” to have the result of doing what we want. But adaptive evolution seems to produce solutions with what amount to intermediate characteristics. There are elements of mechanism to be seen. And there are also usually certain “sparks of computational irreducibility”. Typically what we see is that in the process of adaptive evolution all sorts of computational irreducibility is generated. But to achieve whatever purpose has been defined requires “taming” that irreducibility. And, it seems, introducing the kind of “patches of mechanism” that are characteristic of the mechanoidal behavior we have seen.
That those “patches of mechanism” fit together to achieve an overall purpose is often a surprising thing. But it’s the essence of the kind of “bulk orchestration” that we see in the systems we’ve studied here, and that seems also to be characteristic of biological systems.
Having specified a particular purpose it’s often completely unclear how a given kind of system could possibly achieve it. And indeed what we’ve seen adaptive evolution do here often seems like magic. But in a sense what we’re seeing is just a reflection of the immense power that is available in the computational universe, and manifest in the phenomenon of computational irreducibility. Without computational irreducibility we’d somehow “get what we expect”; computational irreducibility is what adds what is ultimately an infinite element of surprise. And what we’ve seen is that adaptive evolution manages to successfully harness that “element of surprise” to achieve particular purposes.
Let’s say our goal is to generate a particular sequence of values. One might imagine just operating on a space of possible sequences, and gradually adaptively evolving to the sequence we want. But that’s not the setup we’re using here, and it’s not the setup biology has either. Instead what’s happening both in our idealized cellular automaton systems—and in biology—is that the adaptive evolution process is operating at the level of underlying rules, but the purposes are achieved by the results of running those rules. And it’s because of this distinction—which in biology is associated with genotypes vs. phenotypes—that computational irreducibility has a way to insert itself. In some sense both the underlying rules and overall patterns of purposes can be thought of as defining certain “syntactic structures”. The actual running of the rules then represents what one can think of as the “semantics” of the system. And it’s there that the power of computation is injected.
But in the end, just how powerful is adaptive evolution, with its ability to tap into computational irreducibility, and to “mine” the computational universe? We’ve seen that some goals are easier to reach than others. And indeed we introduced the concept of mutational complexity to characterize just how much “effort of adaptive evolution” (and, ultimately, how many mutations)—is needed to achieve a given objective.
If adaptive evolution is able to “fully run its course” then we can expect it to achieve its objective through rules that show mechanoidal behavior and clear “evidence of mechanism”. But if the amount of adaptive evolution stops short of what’s defined by the mutational complexity of the objective, then one’s likely to see more of the “untamed computational irreducibility” that’s characteristic of intermediate stages of adaptive evolution. In other words, if we “get all the way to a solution” there’ll be mechanism to be seen. But if we stop short, there’s likely to be all sorts of “gratuitous complexity” associated with computational irreducibility.
We can think of our final rulial ensemble as consisting of rules that “successfully achieve their purpose”; when we stop short we end up with another, “intermediate” rulial ensemble consisting of rules that are merely on a path to achieve their purpose. In the final ensemble the forces of adaptive evolution have in a sense tamed the forces of computational irreducibility. But in the intermediate ensemble the forces of computational irreducibility are still strong, bringing the various universal features of computational irreducibility to the fore.
It may be useful to contrast all of this with what happens in traditional statistical mechanics, say of molecules in a gas—in which I’ve argued (elsewhere) that there’s in a sense almost always “unchecked computational irreducibility”. And it’s this unchecked computational irreducibility that leads to the Second Law—by producing configurations of the system that we (as computationally bounded observers) can’t distinguish from random, and can therefore reasonably model statistically just as being “typical of the ensemble”, where now the ensemble consists of all possible configurations of the system that, for example, have the same energy or the same temperature. Adaptive evolution is a different story. First, it’s operating not directly on the configurations of a system, but rather on the underlying rules for the system. And second, if one takes the process of adaptive evolution far enough (so that, for example, the number of steps of adaptive evolution is large compared to the mutational complexity of the goal one’s pursuing), then adaptive evolution will “tame” the computational irreducibility. But there’s still an ensemble involved—though now it’s an ensemble of rules rather than an ensemble of configurations. And it’s not an ensemble that somehow “covers all rules”; rather, it’s an ensemble that is “sculpted” by the constraint of “achieving a purpose”.
I’ve argued that it’s the characteristics of “observers like us” that ultimately lead to the perceived validity of the Second Law. So is there a role for the notion of an observer in our discussion here of bulk orchestration and the rulial ensemble? Well, yes. And in particular it’s critical in grounding our concept of “purpose”. We might ask: what possible “purposes” are there? Well, for something to be a reasonable “purpose” there has to be some way to decide whether or not it’s been achieved. And to make such a decision we need something that’s in effect an “observer”.
In the case of statistical mechanics and the Second Law—and, in fact, in all our recent successes in deriving foundational principles in both physics and mathematics—we want to consider observers that are somehow “like us”, because in the end what matters for us is how we as observers perceive things. I’ve argued that the most critical feature of observers like us is that we’re computationally bounded (and also, somewhat relatedly, that we assume we’re persistent in time). And it then turns out that the interplay of these features with underlying computational irreducibility is what seems to lead to the core principles of physics (and mathematics) that we’re familiar with.
But what should we assume about the “observer”—or the “determiner of purpose”—in adaptive evolution, and in particular in biology? It turns out that once again it seems as if computational boundedness is the key. In biological evolution, the implicit “goal” is to have a successful (or “fit”) organism that will, for example, reproduce well in its environment. But the point is that this is a coarse constraint—that we can think of at a computational level as being computationally bounded.
And indeed I’ve recently argued that it’s this computational boundedness that’s ultimately responsible for the fact that biological evolution can work at all. If to be successful an organism always immediately had to satisfy some computationally very complex constraint, adaptive evolution wouldn’t typically ever be able to find the necessary “solution”. Or, put another way, biological evolution works because the objectives it ends up having to achieve are of limited mutational complexity.
But why should it be that the environment in which biological evolution occurs can be “navigated” by satisfying computational bounded constraints? In the end, it’s a consequence of the inevitable presence of pockets of computational reducibility in any ultimately computationally irreducible system. Whatever the underlying structure of things, there will always be pockets of computational reducibility to be found. And it seems that that’s what biology and biological evolution rely on. Specific types of biological organisms are often thought of as populating particular “niches” in the environment defined by our planet; what we’re saying here is that all possible “evolved entities” populate an abstract “meta niche” associated with possible pockets of computational reducibility.
But actually there’s more. Because the presence of pockets of computational reducibility is also what ultimately makes it possible for there to be observers like us at all. As I’ve argued elsewhere, it’s an abstract necessity that there must exist a unique object—that I call the ruliad—that is the entangled limit of all possible computational processes. And everything that exists must somehow be within the ruliad. But where then are we? It’s not immediately obvious that observers like us—with a coherent existence—would be possible within the ruliad. But if we are to exist there, we must in effect exist in some computationally reducible slice of the ruliad. And, yes, for us to be the way we are, we must in effect be in such a slice.
But we can still ask why and how we got there. And that’s something that’s potentially informed by the notion of adaptive evolution that we’ve discussed here. Indeed, we’ve argued that for adaptive evolution to be successful its objectives must in effect be computationally reducible. So as soon as we know that adaptive evolution is operating it becomes in a sense inevitable that it will lead to pockets of computational reducibility. That doesn’t in and of itself explain why adaptive evolution happens—but in effect it shows that if it does, it will lead to observers that at some level have characteristics like us. So then it’s a matter of abstract scientific investigation to show—as we in effect have here—that within the ruliad it’s at least possible to have adaptive evolution.
Any phenomenon can potentially be explained both in terms of purpose and in terms of mechanism. Why does a projectile follow that trajectory? One can explain it as following the mechanism defined by its laws of motion. Or one can explain it as following the purpose of satisfying some overall variational principle (say, extremizing the action associated with the trajectory). Sometimes phenomena are more conveniently explained in terms of mechanism; sometimes in terms of purpose. And one can imagine that the choice could be determined by which is somehow the “computationally simpler” explanation.
But what about the systems and processes we’ve discussed here? If we just run a system like a cellular automaton we always know its “mechanism”—it’s just its underlying rules. But we don’t immediately know its “purpose”, and indeed if we pick an arbitrary rule there’s no reason to think it will have a “computationally simple” purpose. In fact, insofar as the running of the cellular automaton is a computationally irreducible process, we can expect that it won’t “achieve” any such computationally simple purpose that we can identify.
But what if the rule is determined by some process of adaptive evolution? Well, then the objective of that adaptive evolution can be seen as defining a purpose that we can use to describe at least certain aspects of the behavior of the system. But what exactly are the implications of the “presence of purpose” on how the system operates? The key point that’s emerged here is that when there’s a computationally simple purpose that’s been achieved through a process of adaptive evolution, then the rules for the system will be part of what we’ve called the rulial ensemble. And then what we’ve argued is that there are generic features of the rulial ensemble—features that don’t depend on what specific purpose the adaptive evolution might have achieved, only that its purpose was computationally simple. And foremost among these generic features is the presence of mechanoidal behavior.
In other words, so long as there is an overall computationally simple purpose, what we’ve found is that—whatever in detail that purpose might have been—the presence of purpose tends to “push itself down” to produce behavior that locally is mechanoidal, in the sense that it shows evidence of “visible mechanism”. What do we mean by “visible mechanism”? Operationally, it tends to be mechanism that’s readily amenable to “human-level narrative explanation”.
It’s worth remembering that at the lowest level the systems we’ve studied are set up to have simple “mechanisms” in the sense that they have simple underlying rules. But once these rules run they generically produce computationally irreducible behavior that doesn’t have a simple “narrative-like” description. But when we’re looking at the results of adaptive evolution we’re dealing with a subset of rules that are part of the rulial ensemble—and so we end up seeing mechanoidal behavior with at least local “narrative descriptions”.
As we’ve discussed, though, if the adaptive evolution hasn’t “entirely run its course”, in the sense that the mutational complexity of the objective is higher than the actual amount of adaptive evolution that’s been done, then there’ll still be computational irreducibility that hasn’t been “squeezed out”.
So how does all this relate to biology? The first key element of biology as far as we are concerned here is that there’s a separate genotype and phenotype—related by what’s presumably in general the computationally irreducible process of biological growth, etc. The second key element of biology for our purposes here is the phenomenon of self reproduction—in which new organisms are produced with genotypes that are identical up to small mutations. Both these elements are immediately captured by the simple cellular automaton model we’ve used here.
And given them, we seem to be led inexorably to our conclusions here about the rulial ensemble, mechanoidal behavior, and bulk orchestration.
It’s often been seen as mysterious how there ends up being so much apparent complexity in biology. But once one knows about computational irreducibility, one realizes that actually complexity is quite ubiquitous. And instead what’s in many respects more surprising is the presence of any “explainable mechanism”. But what we’ve seen here through the rulial ensemble is that such explainable mechanism is in effect a shadow of overall “simple computational purposes”.
At some level there’s computational irreducibility everywhere. And indeed it’s
the driver for rich behavior. But what happens is that “in the presence of overall purpose”, patches of computational irreducibility have to be fitted together to achieve that purpose. Or, in other words, there’s inevitably a certain “bulk orchestration” of all those patches of computation. And that’s what we see so often in actual biological systems.
So what is it in the end that’s special about life—and biological systems? I think—more than anything—it’s that it’s involved so much adaptive evolution. All those ~1040 individual organisms in the history of life on earth have been links in chains of adaptive evolution. It might have been that all that “effort of adaptive evolution” would have the effect of just “solving the problem”—and producing some “simple mechanistic solution”.
But that’s not what we’ve seen here, and that’s not how we can expect things to work. Instead, what we have is an elaborate interplay of “lumps of computational irreducibility” being “harnessed” by “simple mechanisms”. It matters that there’s been so much adaptive evolution. And what we’re now seeing throughout biology—down to the smallest features—is the consequences of that adaptive evolution. Yes, there are “frozen accidents of history” to be seen. But the point is not those individual items, but rather the whole aggregate consequence of adaptive evolution: mechanoidal behavior and bulk orchestration.
And it’s because these features are generic that we can hope they can form the basis for what amounts to a robust “bulk” theory of biological systems and biological behavior: something that has roughly the same “bulk theory” character as the gas laws, or fluid dynamics. But that’s now talking about systems that have been subject to large-scale adaptive evolution at the level of their rules.
What I’ve done here is very much just a beginning. But I believe the ruliological investigations I’ve shown, and the general framework I’ve described, provide the raw material for something we’ve never had before: a well defined and general “fundamental theory” for the operation of living systems. It won’t describe all the “historical accident” details. But I’m hopeful that it will provide a useful global view of what’s going on, that can potentially be harvested for answers to all sorts of useful questions about the remarkable phenomenon we call life.
In our explorations of the rulial ensemble—and of mutational complexity—we’ve looked at a range of possible objective functions. But we’ve always considered just one adaptive evolution strategy: accepting or rejecting the results of single-point random mutations in the rule at each step. So what would happen if we were to adopt a different strategy? The main conclusion is: it doesn’t seem to matter much. For a particular objective function, there are adaptive evolution strategies that get to a given result in fewer adaptive steps, or that ultimately get further than our usual strategy ever does. But in the end the basic story of the rulial ensemble—and of mutational complexity—is robust relative to detailed changes in our adaptive evolution process.
As an example, consider allowing more than one random mutation in the rule at each adaptive evolution step. Let’s say—as at the very beginning above—that our objective is to generate ![]() after 50 steps. With just one mutation at each step it’s only a small fraction of adaptive evolution “runs” that reach “perfect solutions”, but with more mutations at each step, more progress is made, at least in this case—as illustrated by histograms of the “number of errors” remaining after 10,000 adaptive evolution steps:
after 50 steps. With just one mutation at each step it’s only a small fraction of adaptive evolution “runs” that reach “perfect solutions”, but with more mutations at each step, more progress is made, at least in this case—as illustrated by histograms of the “number of errors” remaining after 10,000 adaptive evolution steps:

Looked at in terms of multiway systems, having fewer mutations at each step leads to fewer paths between possible rules, and a greater possibility of “getting stuck”. With more mutations at each step there are more paths overall, and a lower possibility of getting stuck.
So what about mutational complexity? If we still say that each adaptive evolution step accounts for a single unit of mutational complexity (even if it involves multiple underlying mutations in the rule), this shows how the mutational complexity (as computed above) for different objectives is affected by having different numbers of underlying mutations at each step (the height of each “tick” indicates the number of mutations):
So, yes, different numbers of mutations at each step lead to mutational complexities that are different in detail, but in most cases, surprisingly similar overall.
What about other adaptive evolution strategies? There are many one could consider. For example, a “gradient descent” approach where at each step we examine all possible mutations, and pick the “best one”—i.e. the one that increases fitness the most. (We can extend this by keeping not just the top rule at each step, but, say, the top 5—in an analog of “beam search”.) There’s also a “collaborative” approach, where multiple different “paths” of random mutations are followed, but where every so often all are reset to be the best found so far. And indeed, we can consider all sorts of techniques from reinforcement learning.
In particular cases, any of these approaches can have significant effects. But in general the phenomena we’re discussing here seem robust enough that the details of how adaptive evolution is done don’t matter much, and the single-mutation strategy we’ve mostly used here can be considered adequately representative.
It’s been obvious since antiquity that living organisms contain some kind of “gooey stuff” that’s different from what one finds elsewhere in nature. But what is it? And how universal might it be? In Victorian times it had various names, the most notable being “protoplasm”. The increasing effectiveness of microscopy made it clear that there was actually a lot of structure in “living matter”—as, for example, reflected in the presence of different organelles. But until the later part of the twentieth century there was a general belief that fundamentally what was going on in life was chemistry—or at least biochemistry—in which all sorts of different kinds of molecules were randomly moving and undergoing chemical reactions at certain rates.
The digital nature of DNA discovered in 1953 slowly began to erode this picture, adding in ideas about molecular-scale mechanisms and “machinery” that could be described in mechanical or informational—rather than “bulk statistical”—ways. And indeed a notable trend in molecular biology over the past several decades has been the discovery of more and more ways in which molecular processes in living systems are “actively orchestrated”, and not just the result of “random statistical behavior”.
When a single component can be identified (cell membranes, microtubules, biomolecular condensates, etc.) there’s quite often been “bulk theory” developed, typically based on ideas from statistical mechanics. But when it comes to constellations of different kinds of components, most of what’s been done has been to collect the material to fill many volumes of biology texts with what amount to narrative descriptions of how in detail things operate—with no attempt at any kind of “general picture” independent of particular details.
My own foundational interest in biology goes back about half a century. And when I first started studying cellular automata at the beginning of the 1980s I certainly wondered (as others had before) whether they might be relevant to biology. That question was then greatly accelerated when I discovered that even with simple rules, cellular automata could generate immensely complex behavior, which often looked visually surprisingly “organic”.
In the 1990s I put quite some effort into what amount to macroscopic questions in biology: how do things grow into different shapes, produce different pigmentation patterns, etc.? But somehow in everything I studied there was a certain assumed uniformity: many elements might be involved, but they were all somehow essentially the same. I was well aware of the complex reaction networks—and, later, pieces of “molecular machinery”—that had been discovered. But they felt more like systems from engineering—with lots of different detailed components—and not like systems where there could be a “broad theory”.
Still, within the type of engineering I knew best—namely software engineering—I kept wondering whether there might perhaps be general things one could say, particularly about the overall structure and operation of large software systems. I made measurements. I constructed dependency graphs. I thought about analogies between bugs and diseases. But beyond a few power laws and the like, I never really found anything.
A lot changed, however, with the advent of our Physics Project in 2020. Because, among other things, there was now the idea that everything—even the structure of spacetime—was dynamic, and in effect emerged from a graph of causal relationships between events. So what about biology? Could it be that what mattered in molecular biology was the causal graph of interactions between individual molecules? Perhaps there needed to be a “subchemistry” that tracked specific molecules, rather than just molecular species. And perhaps to imagine that ordinary chemistry could be the basis for biology was as wide of the mark as thinking that studying the physics of electron gases would let one understand microprocessors.
Back in the early 1980s I had identified that the typical behavior of systems like cellular automata could be divided into four classes—with the fourth class having the highest level of obvious complexity. And, yes, the visual patterns produced in class 4 systems often had a very “life like” appearance. But was there a foundational connection? In 2023, as part of closing off a 50-year personal journey, I had been studying the Second Law of thermodynamics, and identified class 4 systems as ones that—like living systems—aren’t usefully described just in terms of a tendency to randomization. Reversible class 4 systems made it particularly clear that in class 4 there really was a distinct form of behavior—that I called “mechanoidal”—in which a certain amount of definite structure and “mechanism” are visible, albeit embedded in great overall complexity.
At first far from thinking about molecules I made some surprise progress in 2024 on biological evolution. In the mid-1980s I had considered modeling evolution in terms of successive small mutations to things like cellular automaton rules. But at the time it didn’t work. And it’s only after new intuition from the success of machine learning that in 2024 I tried again—and this time it worked. Given an objective like “make a finite pattern that lives as long as possible”, adaptive evolution by successive mutation of rules (say in a cellular automaton) seemed to almost magically find—typically very elaborate—solutions. Soon I had understood that what I was seeing was essentially “raw computational irreducibility” that just “happened” to fit the fairly coarse fitness criteria I was using. And I then argued that the success of biological evolution was the result of the interplay between computationally bounded fitness and underlying computational irreducibility.
But, OK, what did that mean for the “innards” of biological systems? Exploring an idealized version of medicine on the basis of my minimal models of biological evolution led me to look in a bit more detail at the spectrum of behavior in adaptively evolved systems, and in variants produced by perturbations.
But was there something general—something potentially universal—that one could say? In the Second Law one often talks about how behavior one sees is somehow overwhelmingly likely to be “typical of the ensemble of all possibilities”. In the usual Second Law, the possibilities are just different initial configurations of molecules, etc. But in thinking about a system that can change its rules, the ensemble of all possibilities is—at least at the outset—much bigger: in effect it’s the whole ruliad. But the crucial point I realized a few months ago is that the changes in rules that are relevant for biology must be ones that can somehow be achieved by a process of adaptive evolution. But what should the objective of that adaptive evolution be?
One of the key lessons from our Physics Project and the many things informed by it is that, yes, the character of the observer matters—but knowing just a little about an observer can be sufficient to deduce a lot about the laws of behavior that observer will perceive. So that led to the idea that this kind of thing might be true about objective functions—and that just knowing that, for example, an objective function is computationally simple might be enough to tell one things about the “rulial ensemble” of possible rules.
But is that really true? Well, as I have done so many times, I turned to computer experiments to find out. In my work on the foundations of biological evolution I had used what are in a sense very “generic” fitness functions (like overall lifetime). But now I needed a whole spectrum of possible fitness functions—some of them by many measures in fact even simpler to set up than something like lifetime.
The results I’ve reported here I consider very encouraging. The underlying details don’t seem to matter much. But a broad range of computationally simple fitness functions seem to “worm their way down” to have the same kind of effect on small-scale behavior—and to make it in some sense mechanoidal.
Biology has tended to be a field in which one doesn’t expect much in the way of formal theoretical underpinning. And indeed—even after all the data that’s been collected—there are remarkably few “big theories” in biology: natural selection and the digital/informational nature of DNA have been pretty much the only examples. But now, from the type of thinking introduced by our Physics Project, we have something new and different: the concept of the rulial ensemble, and the idea that essentially just from the fact of biological evolution we can talk about certain features of how adaptively evolved systems in biology must work.
Traditional mathematical methods have never gotten very far with the broad foundations of biology. And nor, in the end, has specific computational modeling. But by going to a higher level—and in a sense thinking about the space of all possible computations—I believe we can begin to see a path to a powerful general framework not only for the foundations of biology, but for any system that shows bulk orchestration produced by a process of adaptive evolution.
Thanks to Willem Nielsen of the Wolfram Institute for extensive help, as well as to Wolfram Institute affiliates Júlia Campolim and Jesse Angeles Lopez for their additional help. The ideas here have ultimately come together rather quickly, but in both the recent and the distant past discussions with a number of people have provided useful ideas and background—including with Richard Assar, Charles Bennett, Greg Chaitin, Paul Davies, Walter Fontana, Nigel Goldenfeld, Greg Huber, Stuart Kauffman, Chris Langton, Pedro Márquez-Zacarías and Elizabeth Wolfram.
2025-09-16 03:20:59
![]()
Click any diagram to get Wolfram Language code to reproduce it.
It’s a story of pure, abstract computation. In fact, historically, one of the very first. But even though it’s something I for one have used in practice for nearly half a century, it’s not something that in all my years of exploring simple computational systems and ruliology I’ve ever specifically studied. And, yes, it involves some fiddly technical details. But it’ll turn out that lambdas—like so many systems I’ve explored—have a rich ruliology, made particularly significant by their connection to practical computing.
In Wolfram Language it’s the Function function. Back when Alonzo Church first discussed it in the 1930s he called it λ (lambda). The idea is to have something that serves as a “pure function”—which can be applied to an argument to give a value. For example, in the Wolfram Language one might have:
On its own it’s just a symbolic expression that evaluates to itself. But if we apply it to an argument then it substitutes that argument into its body, and then evaluates that body:
In the Wolfram Language we can also write this as:
Or, with λ = Function, we can write
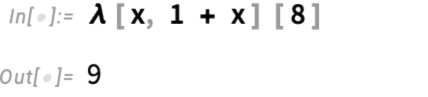
which is close to Church’s original notation (λx .(1 + x)) 8.
But what if we want to “go even purer”, and effectively just “use λ for everything”—without any pre-defined functions like Plus (+)? To set up lambdas at all, we have to have a notion of function application (as in f[x] meaning “apply f to x”). So, for example, here’s a lambda (“pure function”) that just has a structure defined by function application:
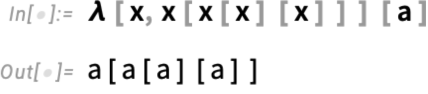
Can we do familiar operations with this kind of setup? Let’s imagine we have a symbol z that represents 0, and another symbol s that represents the operation of computing a successor. Then here’s a representation of the integers 0 through 5:
But let’s look for example at s[s[s[s[z]]]]. We can “factor out” the s and z in this expression and write the “purely structural” part just in terms of lambdas:
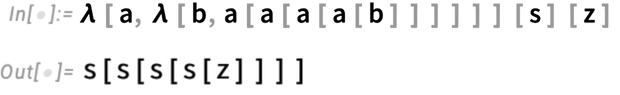
But in a sense we don’t need the s and z here; we can perfectly well set up a representation for integers just in terms of lambdas, say as (often known as “Church numerals”):
It’s all very pure—and abstract. And, at least at first, it seems very clean. But pretty soon one runs into a serious problem. If we were to write
what would it mean? In x[x] are the x’s associated with the x in the inner λ or the outer one? Typing such an expression into the Wolfram Language, x’s turn red to indicate that there’s a problem:
And at this level the only way to resolve the problem is to use different names for the two x’s—for example:
But ultimately the particular names one uses don’t matter. For example, swapping x and y
represents exactly the same function as before.
How can one deal with this? One approach—that was actually invented more than a decade before lambdas, and that I in fact wrote a whole book about a few years ago—is to use so-called “combinators”: constructs S and K that in effect abstractly define how to rearrange symbolic expressions, without having to name anything, or, for that matter, introduce variables at all. So, for example, λ[x, λ[y, y[x]]] can be written
as one can confirm using:
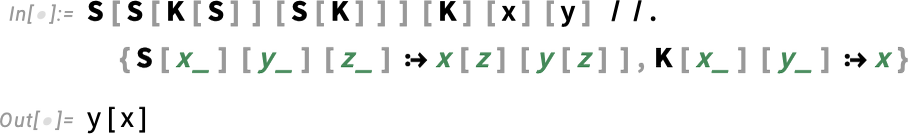
At some level this is very elegant. But, yes, it’s extremely difficult to read. So is there a way to preserve at least some of the comparative readability of lambdas without having to explicitly introduce variables with names, etc.? It turns out there is. And it starts from the observation that a named variable (say x) is basically just a way of referring back to the particular lambda (say λ[x, …]) that introduced that variable. And the idea is that rather than making that reference using a named variable, we make it instead by saying “structurally” where the lambda is relative to whatever is referring to it.
So, for example, given
we can write this in the “de Bruijn index” (pronounced “de broin”) form
where the 1 says that the variable in that position is associated with the λ that’s “one λ back” in the expression, while that 2 says that the variable in that position is “two λ’s back” in the expression:
So, for example, our version of the integers as lambdas can now be written as:
OK, so lambdas can represent things (like integers). But can one “compute with lambdas”? Or, put another way, what can pure lambdas do?
Fundamentally, there’s just one operation—usually called beta reduction—that takes whatever argument a lambda is given, and explicitly “injects it” into the body of the lambda, in effect implementing the “structural” part of applying a function to its argument. A very simple example of beta reduction is
which is equivalent to the standard Wolfram Language evaluation:
In terms of de Bruijn indices this becomes
which can again be “evaluated” (using beta reduction) to be:
This seems like a very simple operation. But, as we’ll see, when applied repeatedly, it can lead to all sorts of complex behavior and interesting structure. And the key to this turns out to be the possibility of lambdas appearing as arguments of other lambdas, and through beta reduction being injected into their bodies.
But as soon as one injects one lambda into another, there are tricky issues that arise. If one writes everything explicitly with variables, there’s usually variable renaming that has to be done, with, for example
evaluating to:
In terms of de Bruijn indices there’s instead renumbering to be done, so that
evaluates to:
It’s easy to describe informally what beta reduction is doing. In Wolfram Language terms it’s basically just the transformation:
In other words, given λ[x, body][y], beta reduction is replacing every instance of x in body with y, and returning the result. But it’s not quite as simple as that. For example, if y contains a lambda—as in the example above—then we may have to do a certain amount of renaming of variables (usually called “alpha conversion”). And, yes, there can potentially be a cascade of renamings. And you might have to come up with an arbitrary number of distinct new names to use in these renamings.
And once you’ve done the substitution (“beta reduction”) of λ[x, body][y] this can “expose” another lambda in which you have to do more substitution, and so on. This might sound like a detail. But actually it’s quite fundamental—and it’s what lets lambdas represent computations that “keep running”, and that give rise to the rich ruliology we’ll discuss here.
Is it somehow easier to do beta reduction with de Bruijn indices? No, not really. Yes, you don’t have to invent names for variables. But instead you have to do rather fiddly recursive realignment of indices whenever you’re in effect inserting or deleting lambdas.
There’s another issue as well. As we’ll explore in detail later, there are often multiple beta reductions that can be done on a given lambda. And if we trace all the possibilities we get a whole multiway graph of possible “paths of lambda evaluation”. But a fundamental fact about lambdas (known as confluence or the Church–Rosser property, and related to causal invariance) is that if a sequence of beta reductions for a given lambda eventually reaches a fixed point (which, as we’ll see, it doesn’t always), that fixed point will be unique: in other words, evaluating the lambda will always give a definite result (or “normal form”).
So what should one call the things one does when one’s working with lambdas? In Wolfram Language we talk of the process of, say, turning Function[x, x[x]][a] (or λ[x, x[x]][a]) into a[a] as “evaluation”. But sometimes it’s instead called, for example, reduction or conversion or substitution or rewriting. In Wolfram Language we might also call λ[…] a “λ expression”, but it’s also sometimes called a λ term. What about what’s inside it? In λ[x, body] the x is usually called a “bound variable”. (If there’s a variable—say y—that appears in body and that hasn’t been “bound” (or “scoped”) by a λ, it’s called a “free variable”. The λ expressions that we’ll be discussing here normally have no free variables; such λ expressions are often called “closed λ terms”. )
Putting a lambda around something—as in λ[x, thing]—is usually called “λ abstraction”, or just “abstraction”, and the λ itself is sometimes called the “abstractor”. Within the “body” of a lambda, applying x to y to form x[y] is—not surprisingly—usually called an “application” (and, as we’ll discuss later, it can be represented as x@y or x•y). What about operations on lambdas? Historically three are identified: α reduction (or α conversion), β reduction (or β conversion) and η reduction (or η conversion). β reduction—which we discussed above—is really the core “evaluation-style” operation (e.g. replacing λ[x, f[x]][y] with f[y]). α and η reduction are, in a sense, “symbolic housekeeping operations”; α reduction is the renaming of variables, while η reduction is the reduction of λ[x, f[x]] to f alone. (In principle one could also imagine other reductions—say transformations directly defined for λ[_][_][_]—though these aren’t traditional for lambdas.)
The actual part of a lambda on which a reduction is done is often called a “redex”; the rest of the lambda is then the “context”—or “an expression with a hole”. In what we’ll be doing here, we’ll mostly be concerned with the—fundamentally computational—process of progressively evaluating/reducing/converting/… lambdas. But a lot of the formal work done in the past on lambdas has concentrated on the somewhat different problem of the “calculus of λ conversion”—or just “λ calculus”—which concentrates particularly on identifying equivalences between lambdas, or, in other words, determining when one λ expression can be converted into another, or has the same normal form as another.
By the way, it’s worth saying that—as I mentioned above—there’s a close relationship between lambdas and the combinators about which I wrote extensively a few years ago. And indeed many of the phenomena that I discussed for combinators will show up, with various modifications, in what I write here about lambdas. In general, combinators tend to be a bit easier to work with than lambdas at a formal and computational level. But lambdas have the distinct advantage that at least at the level of individual beta reductions it’s much easier to interpret what they do. The S combinator works in a braintwisting kind of way. But a beta reduction is effectively just “applying a function to an argument”. Of course, when one ends up doing lots of beta reductions, the results can be very complicated—which is what we’ll be talking about here.
How can one do familiar computations just using lambdas? First, we need a way to represent things purely in terms of lambdas. So, for example, as we discussed above, we can represent integers using successive nesting. But now we can also define an explicit successor function purely in terms of lambdas. There are many possible ways to do this; one example is
where this is equivalent to:
Defining zero as
or
we can now form a representation of the number 3:
But “evaluating” this by applying beta reduction this turns out to reduce to
which was exactly the representation of 3 that we had above.
Along the same lines, we can define
(where these functions take arguments in “curried” form, say, times[3][2], etc.).
So then for example 3×2 becomes

which evaluates (after 37 steps of beta reduction) to:
Applying this to “unevaluated” s and z we get
which under beta reduction gives
which we can recognize as our representation for the number 6.
And, yes, we can go further. For example, here’s a representation (likely not the absolutely minimal one) for the factorial function in terms of pure lambdas:
And with this definition
i.e. 4!, indeed eventually evaluates to 24:
Later on we’ll discuss the process of doing an evaluation like this and we’ll see that, yes, it’s fairly complicated. In the default way we’ll carry out such evaluations, this particular one takes 103 steps (for successive factorials, the number of steps required is 8, 13, 31, 103, 463, 2623, …).
From what we’ve seen so far, one obvious observation about lambdas is that—except in trivial cases—they’re pretty hard to read. But do they need to be? There are lots of ways to write—and render—them. But what we’ll find is that while different ones have different features and advantages (of which we’ll later make use), none of them really “crack the code” of making lambdas universally easy for us to read.
Let’s consider the following lambda, written out in our standard textual way:
This indicates how the variables that appear are related:
And, yes, since each λ “scopes” its bound variable, we could as well “reuse” y in place of z:
One obvious thing that makes an expression like this hard to read is all the brackets it contains. So how can we get rid of these? Well, in the Wolfram Language we can always write f@x in place of f[x]:
And, yes, because the @ operator in the Wolfram Language associates to the right, we can write f@g@x to represent f[g[x]]. So, OK, using @ lets us get rid of quite a few brackets. But instead it introduces parentheses. So what can we do about these? One thing we might try is to use the application operator • (Application) instead of @, where • is defined to associate to the left, so that f•g•x is f[g][x] instead of f[g[x]]. So in terms of • our lambda becomes:
The parentheses moved around, but they didn’t go away.
We can make these expressions look a bit simpler by using spaces instead of explicit @ or •. But to know what the expressions mean we have to decide whether spaces mean @ or •. In the Wolfram Language, @ tends to be much more useful than • (because, for example, f@g@x conveniently represents applying one function, then another). But in the early history of mathematical logic, spaces were effectively used to represent •. Oh, and λ[x, body] was written as λx . body, giving the following for our example lambda:
We’ve been trying to write lambdas out in linear form. But in some sense, they’re always really trees—just like expressions in the Wolfram Language are trees. So here for example is
shown as a tree:
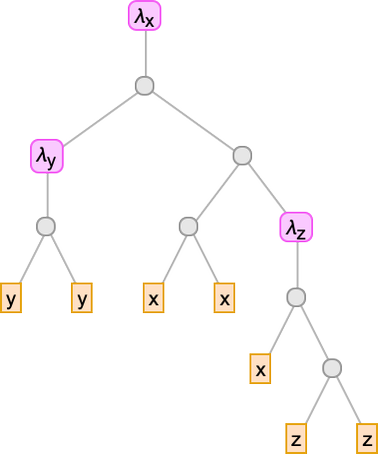
The leaves of the tree are variables. The intermediate nodes are either λ[…, …]’s (“abstractions”) or …[…]’s (“applications”). Everything about lambdas can be done in this tree representation. So, for example, beta reduction can be thought of as a replacement operation on a piece of the tree representing a lambda:
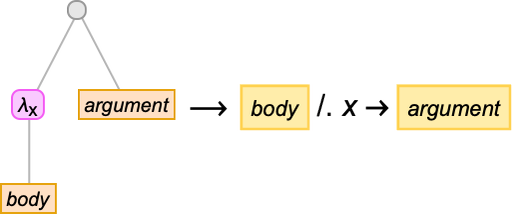
But, OK, as we discussed above, it never matters what specific names have been given to the variables. All that matters is what lambdas they’re associated with. And we can indicate this by overlaying appropriate connections on the tree:

But what if we just route these connections along the branches in the tree?
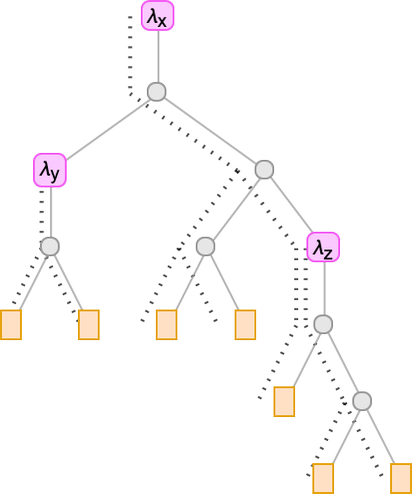
To find out which λ a given variable goes with, we just have to count how many λ’s we encounter walking up the tree from the leaf representing that variable before we reach “its λ”. So this means we can represent the lambda just by filling in a number at each leaf of the tree:
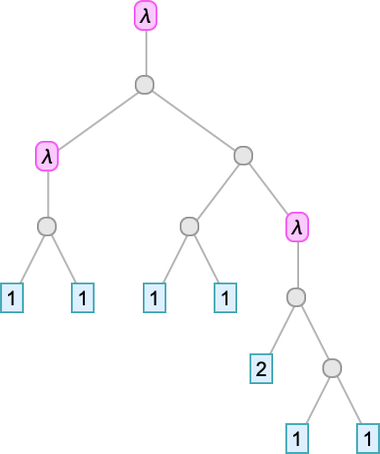
And these numbers are precisely the de Bruijn indices we discussed earlier. So now we’ve seen that we can replace our “named variables” lambda tree with a de Bruijn index lambda tree.
Writing this particular tree out as an expression we get:
The λ’s now don’t have any explicit variables specified. But, yes, the expression is “hooked up” the same way it was when we were explicitly using variables:
Once again we can get rid of our “application brackets” by using the • (Application) operator:
And actually we don’t really need either the •’s or even the λ’s here: everything can be deduced just from the sequence of brackets. So in the end we can write our lambda out as
where there’s an “implicit λ” before every “[” character, and an implicit • between every pair of digits. (Yes, we’re only dealing with the case where all de Bruijn indices are below 10.)
So now we have a minimal way to write out a lambda as a string of characters. It’s compact, but hard to decode. So how can we do better?
At the very simplest level, we could, for example, color code every character (here with explicit λ’s and brackets included):
And indeed we’ll find this representation useful later.
But any “pure string” makes the nesting structure of the lambda visible only rather implicitly, in the sequence of brackets. So how can we make this more explicit? Well, we could explicitly frame each nested λ:
Or we could just indicate the “depth” of each element—either “typographically”
or graphically (where the depth is TreeDepth):

We can think of this as a kind of one-dimensionally-unrolled version of a tree representation of lambdas. Another approach is in effect to draw the tree on a 2D grid—to form what we can call a Tromp diagram:
To see what’s going on here, we can superimpose our standard tree on the Tromp diagram:

Each vertical line represents an instance of a variable. The top of the line indicates the λ associated with that variable—with the λ being represented by a horizontal line. When one instance of a variable is applied to another, as in u[v], there is a horizontal line spanning from the “u” vertical line to the “v” one.
And with this setup, here are Tromp diagrams for some small lambdas:
Another graphical approach is to use “string diagrams” that directly show how the elements of lambdas are “wired up”. Consider for example the simple lambda:
This can be represented as the string diagram:
The connectivity here is the same as in:
In the string diagram, however, the explicit variables have been “squashed out”, but are indicated implicitly by which λ’s the lines connect back to. At each λ node there is one outgoing edge that represents the argument of the λ, and one incoming edge that connects to its body. Just as when we represent the lambda with a tree, the “content” of the lambda “hangs off” the top of the diagram.
Here are examples of string diagrams for a few small lambdas:
In these diagrams, the edges that “exit the diagram” at the bottom correspond to variables that are unused in the lambda. The “cups” that appear in the diagrams correspond to “variables that are immediately used”, as in λ[x, x]. What about the ![]() in, for example, λ[a,λ[b,b[b]]]? It represents the copying of a variable, which is needed here because b is used twice in the lambda.
in, for example, λ[a,λ[b,b[b]]]? It represents the copying of a variable, which is needed here because b is used twice in the lambda.
Returning to our previous example (now written with explicit variables)
here is the (somewhat complicated) string diagram corresponding to this lambda:
One can think of a string diagram like this as somehow defining the “flow of symbolic content” through “pipes” associated with variables. But is there some purer way to represent such flows, without ever having to introduce variables? Well, yes there is, and it’s to use combinators. And indeed there’s an immediate correspondence between combinator expressions and lambdas. So, for example
can be represented in terms of combinators by:
As is typical of combinators, this is in a sense very pure and uniform, but it’s also very difficult to interpret. And, yes, as we’ll discuss later, small lambda expressions can correspond to large combinator expressions. And the same is true the other way around, so that, for example, ![]() becomes as a lambda expression
becomes as a lambda expression
or in compact form:
But, OK, this compact form is in some sense a fairly efficient representation. But it has some hacky features. Like, for example, if there are de Bruijn indices whose values are more than one digit long, they’ll need to be separated by some kind of “punctuation”.
But what if we insist on representing a lambda expression purely as a sequence of 0’s and 1’s? Well, one thing we can do is to take our compact form above, represent its “punctuation characters” by fixed strings, and then effectively represent its de Bruijn indices by numbers in unary—giving for our example above:
This procedure can be thought of as providing a way to represent any lambda by an integer (though it’s certainly not true that it associates every integer with a lambda).
To begin our ruliological investigation of lambdas and what they do, we need to discuss what possible forms of lambdas there are—or, in other words, how to enumerate lambda expressions. An obvious strategy is to look at all lambda expressions that have progressively greater sizes. But what is the appropriate measure of “size” for a lambda expression?
Mostly here we’ll use Wolfram Language LeafCount. So, for example
will be considered to have “size” 10 because in the most direct Wolfram Language tree rendering
there are 10 “leaves”. We’ll usually render lambdas instead in forms like
in which case the size is the number of “de Bruijn index leaves” or “variable leaves” plus the number of λ’s.
(Note that we could consider alternative measures of size in which, for example, we assign different weights to abstractions (λ’s) and to applications, or to de Bruijn index “leaves” with different values.)
Using LeafCount as our measure, there are then, for example, 14 lambdas of size 4:
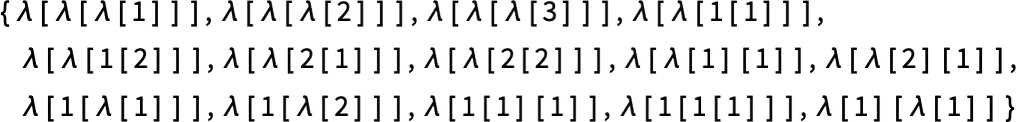
As trees these become
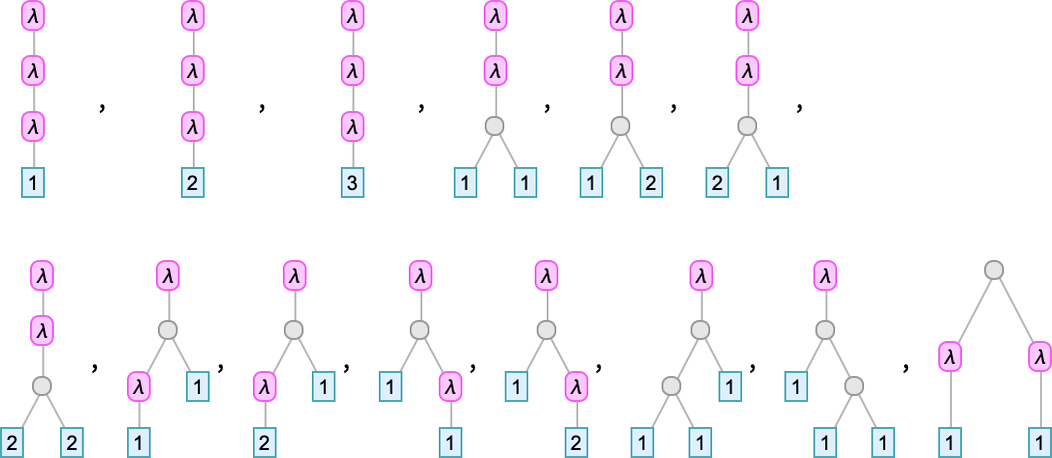
while as Tromp diagrams they are:
The number of lambdas grows rapidly with size:
These numbers are actually given by c[n,0] computed from the simple recurrence:
For large n, this grows roughly like n!, though apparently slightly slower.
At size n, the maximum depth of the expression tree is n – 1; the mean is roughly 3 + n/4 and the limiting distribution is:
We can also display the actual forms of the lambdas, with a notable feature being the comparative diversity of forms seen:

What does it mean to “evaluate” a lambda? The most obvious interpretation is to do a sequence of beta reductions until one reaches a “fixed point” where no further beta reduction can be done.
So, for example, one might have:
If one uses de Bruijn indices, beta reduction becomes a transformation for λ[_][_], and our example becomes:
In compact notation this is
while in terms of trees it is:
By rendering the characters in the de Bruijn index form as color squares, we can also represent this evolution in the “spacetime” form:
But what about other lambdas? None of the lambdas of size 3
contain the pattern λ[_][_], and so none of them allow beta reduction. At size 4 the same is true of most of the 14 possible lambdas, but there is one exception, which allows a single step of beta reduction:
At size 5, 35% of the lambdas aren’t inert, but they still have short “lifetimes”
with the longest “evaluation chain” being:
At size 6, 44% of lambdas allow beta reductions, and aren’t immediately inert:
A couple of lambdas have length-4 evaluation chains:
And now there’s something new—a period-1 “looping lambda” (or “quine”) that just keeps on transforming into itself under beta reduction, and so never reaches a fixed point where no beta reduction can be applied:
At size 7, just over half of the lambdas aren’t inert:
There are a couple of “self-repeating” lambdas:
The first is a simple extension of the self-repeating lambda at size 6; the second is something at least slightly different.
At size 7 there are also a couple of cases where there’s a small “transient” before a final repeating state is reached (here shown in compact form):

Here’s what happens with the lambda trees in this case—where now we’ve indicated in red the part of each tree involved in each beta reduction:
And there’s also something new: three cases where beta reduction leads to lambdas that grow forever. The simplest case is
which grows in size by 1 at each step:


Then there’s
which, after a single-step transient, grows in size by 4 at each step:

And finally there’s
which grows in a slightly more complicated way



alternating between growing by 4 and by 12 on successive steps (so at step t > 1 it is of size 8t – 4 Mod[t + 1, 2]):
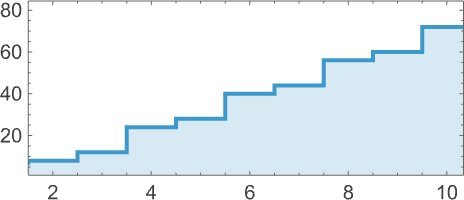
If we look at what’s happening here “underneath”, we see that beta reduction is just repeatedly getting applied to the first λ at each step:
And we can conveniently indicate this when we plot the successive sizes of lambdas:
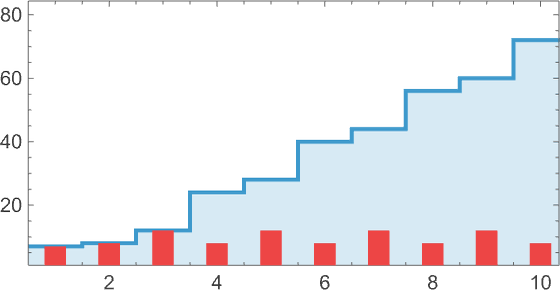
At size 8, things begin to get more interesting. Of the 43,977 possible lambdas, 55% aren’t inert:
The longest evaluation chain that terminates occurs for
and is of length 12:
Among all 43,977 size-8 lambdas, there are only 164 distinct patterns of growth:
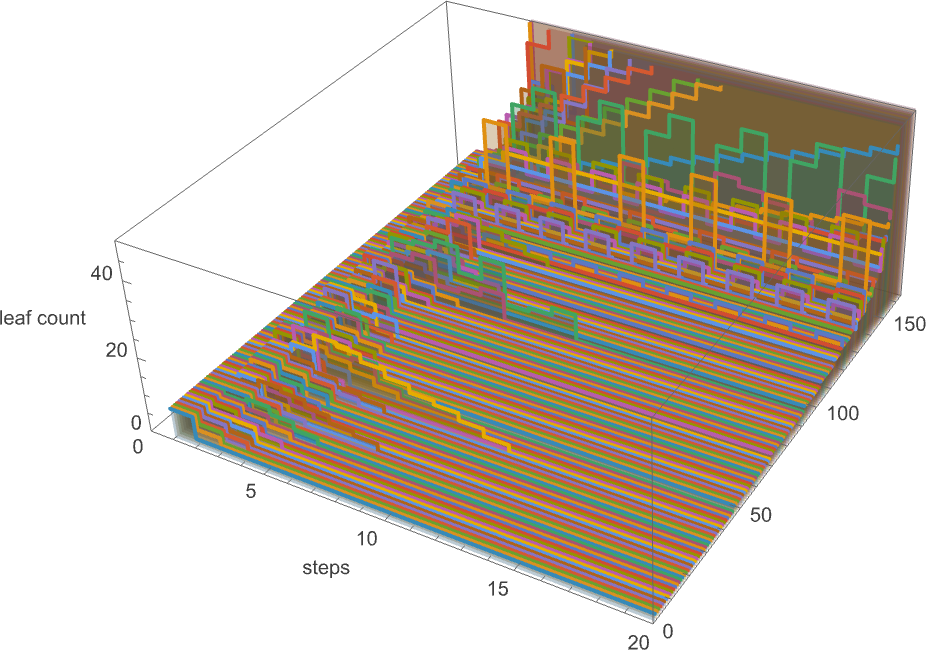
The 81 lambdas that don’t terminate have various patterns of growth:
Some, such as
alternate every other step:
Others, such as
have period 3:
Sometimes, as in
there’s a mixture of growth and periodicity:



There’s simple nested behavior, as in


where the envelope grows like ![]() .
.
There’s more elaborate nested behavior in


where now the envelope grows linearly with t.
Finally, there’s
which instead shows highly regular ![]() growth:
growth:


And the conclusion is that for lambdas up to size 8, nothing more complicated than nested behavior occurs. And in fact in all these cases it’s possible to derive exact formulas for the size at step t.
To see roughly how these formulas work, we can start with the sequence:
This sequence turns out to be given by the nestedly recursive recurrence
and the tth term here is just:
For the first nested sequence above, the corresponding result is (for t > 1):
For the second one it is (for t > 3):
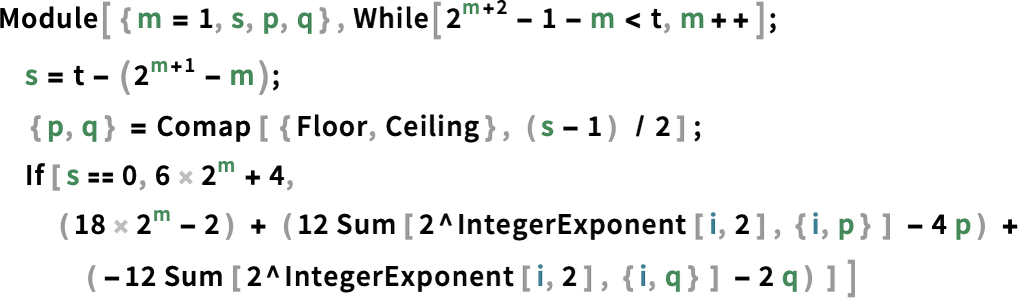
And for the third one it is (for t > 1):
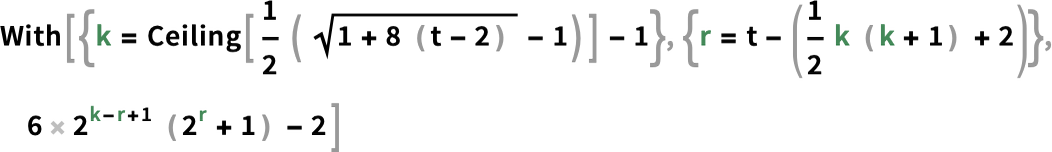
And, yes, it’s quite remarkable that these formulas exist, yet are as comparatively complicated as they are. In effect, they’re taking us a certain distance to the edge of what can be captured with traditional mathematics, as opposed to being findable only by irreducible computation.
We’ve looked systematically at lambdas up to size 8. So what happens with larger lambdas?
At size 9 there are 454,283 possible lambdas. Now the distribution of lifetimes is:


The longest finite lifetime—of 55 steps—occurs for
which eventually evolves to just:
Here are the sizes of the lambdas obtained at each step:
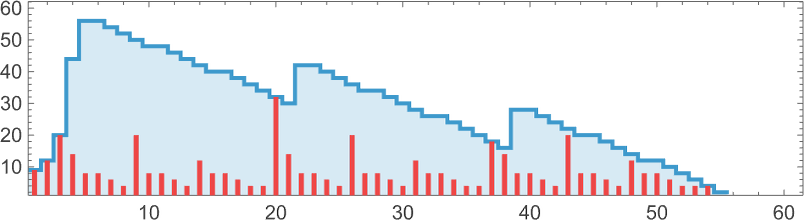
But why does this particular process terminate? It’s not easy to see. Looking at the sequence of trees generated, there’s some indication of how branches rearrange and then disappear:
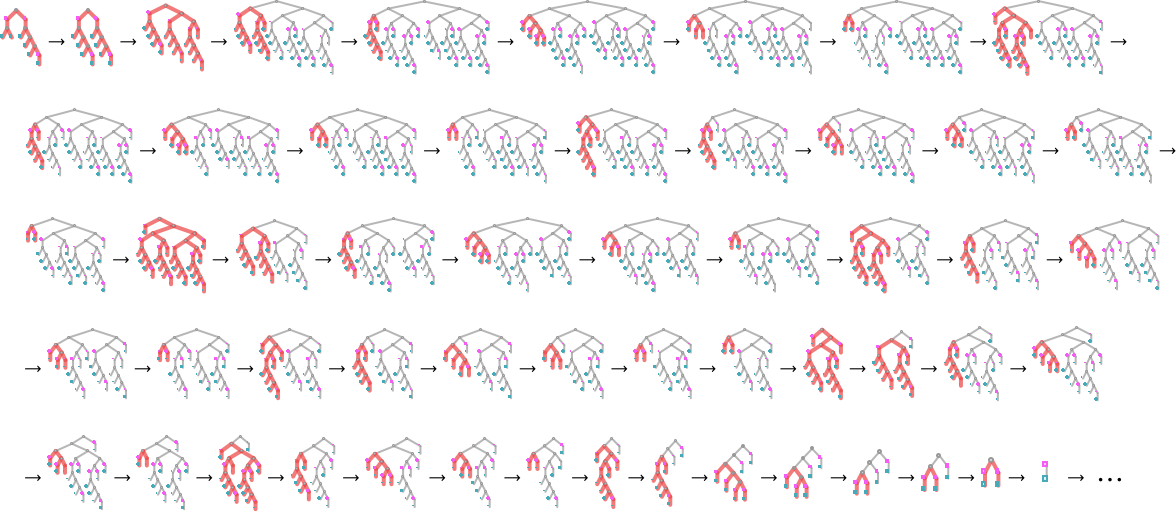
The array plot isn’t very illuminating either:
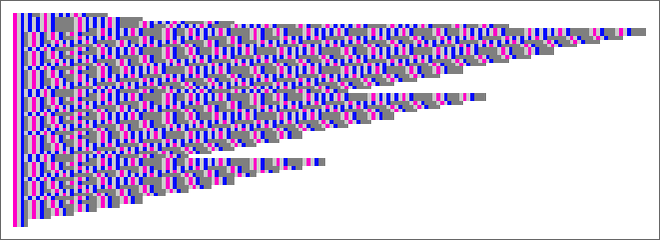
As is so often the case, it doesn’t seem as if there’s any “identifiable mechanism” to what happens; it “just does”.
The runner-up for lifetime among length-9 lambdas—with lifetime 44—is
which eventually evolves to
(which happens to correspond to the integer 16 in the representation we discussed above):
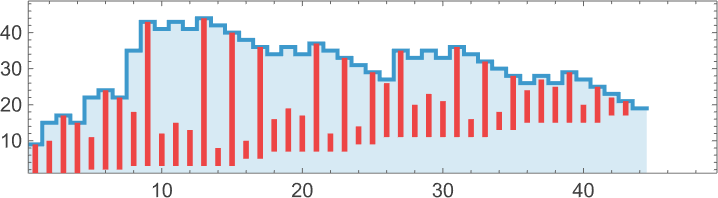
Viewed in “array” form, there’s at least a hint of “mechanism”: we see that over the course of the evolution there’s a steady (linear) increase in the quantity of “pure applications” without any λ’s to “drive things”:

Of the 748 size-9 lambdas that grow forever, most have ultimately periodic patterns of growth. The one with the longest growth period (10 steps) is
which has a rather unremarkable pattern of growth:
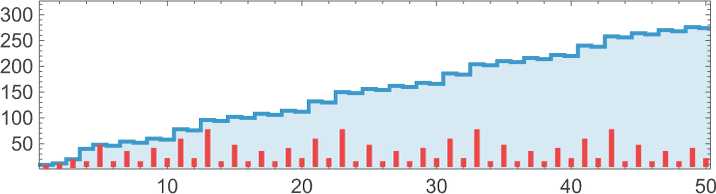

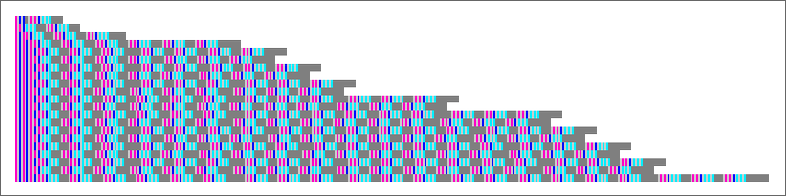
Only 35 lambdas have more complicated patterns of growth:

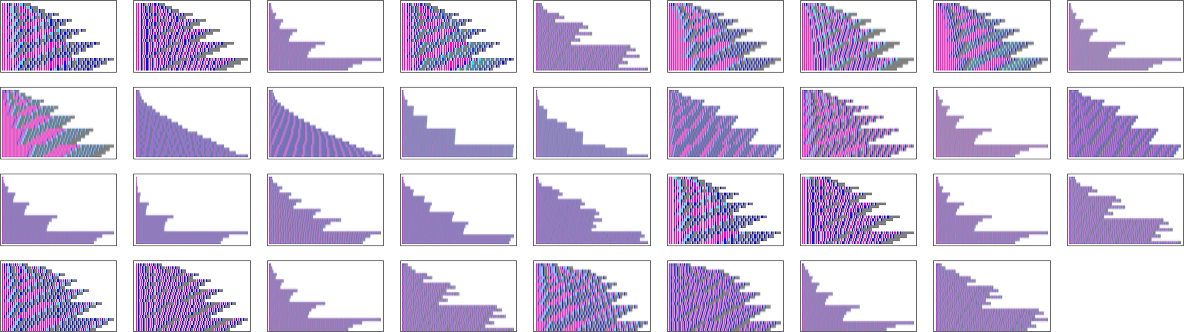
Many have behavior similar to what we saw with size 8. There can be nested patterns of growth, with an envelope that’s linear:

There can be what’s ultimately pure exponential ![]() growth:
growth:
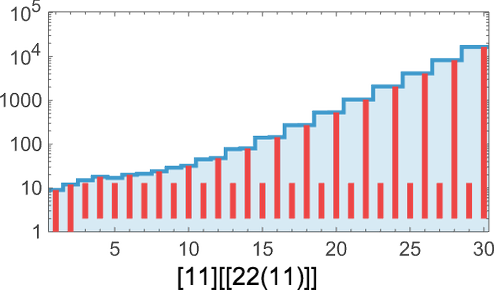
There can also be slower but still exponential growth, in this case ![]() :
:
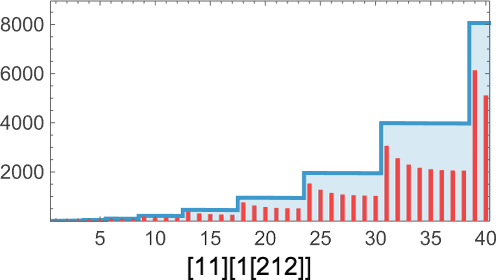

There’s growth that at first looks like it might be complicated, but eventually ends up linear:
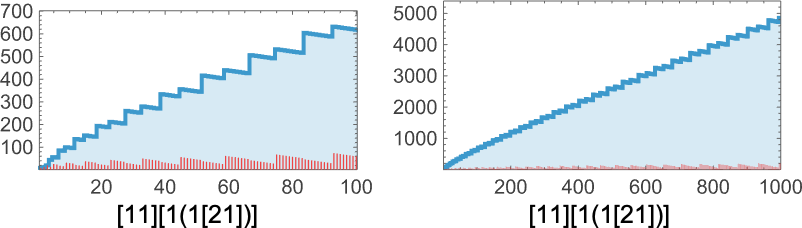
Then there’s what might seem to be irregular growth:

But taking differences reveals a nested structure

even though there’s no obvious nested structure in the detailed pattern of lambdas in this case:

And that’s about it for size 9.
OK, what about size 10? There are now 5,159,441 possible lambdas. Of these, 38% are inert and 0.15% of them don’t terminate. The distribution of lifetimes is:

Some examples of lambdas with long lifetimes are:
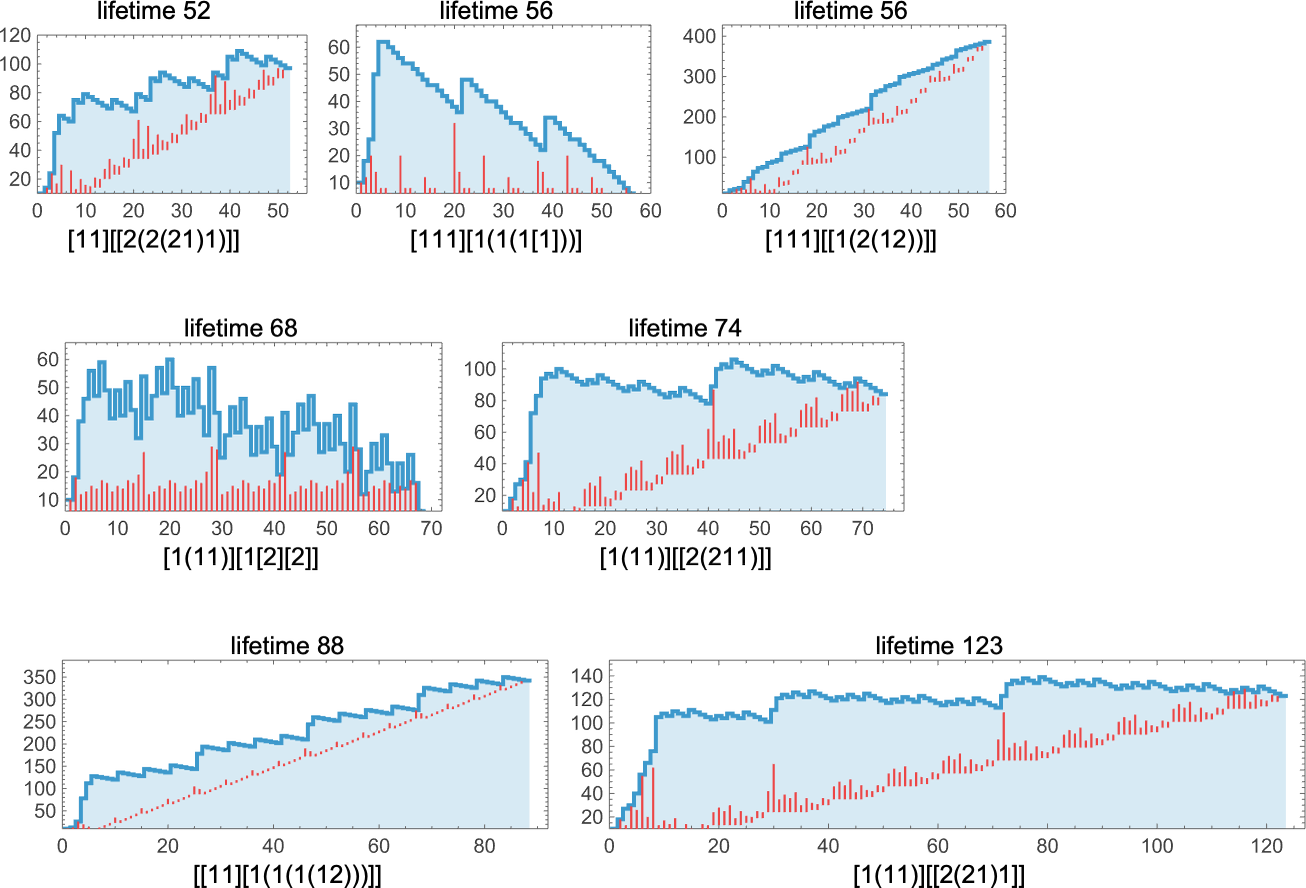
Some of these terminate with small lambdas; the one with lifetime 88 yields a lambda of size 342, while the second one with lifetime 56 yields one of size 386:
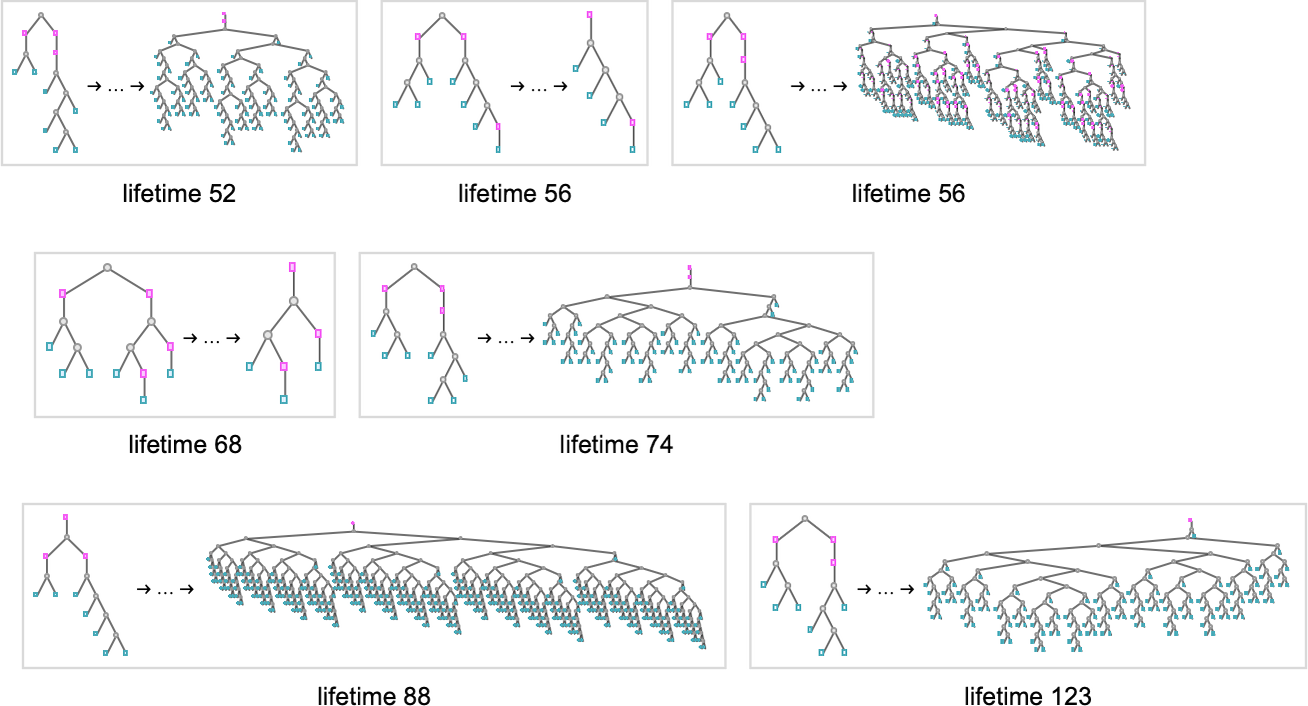
All of these work in somewhat different ways. In some cases the behavior looks quite systematic, and it’s at least somewhat clear they’ll eventually halt; in others it’s not at all obvious:
It’s notable that many, though not all, of these evolutions show linearly increasing “dead” regions, consisting purely of applications, without any actual λ’s—so that, for example, the final fixed point in the lifetime-123 case is:

What about other cases? Well, there are surprises. Like consider:
Running this, say, for 2000 steps it seems to be just uniformly growing:

But then, suddenly, after 3779 steps, there’s a surprise: it terminates—leaving a lambda of size 4950:
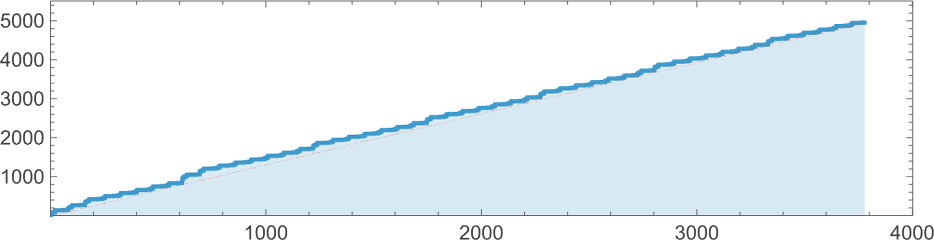
Looking at successive size differences doesn’t give any obvious “advance warning” of termination:
But if one looks at the actual sequence of lambdas generated (here just for 200 steps) we see what appears to be a somewhat telltale buildup of “dead” applications:

And, indeed, in the next section, we’ll see an even longer-lived example.
Even though it’s sometimes had to tell whether the evaluation of a lambda will terminate, there are plenty of cases where it’s obvious. An example is when the evaluation chain ultimately becomes periodic. At size 10, there are longer periods than before; here’s an example with period 27:
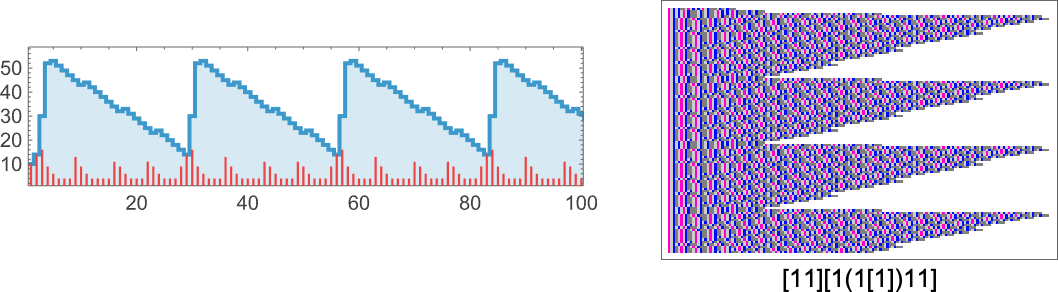
There’s also growth where the sequence of sizes has obvious nested structure—with a linearly growing envelope:
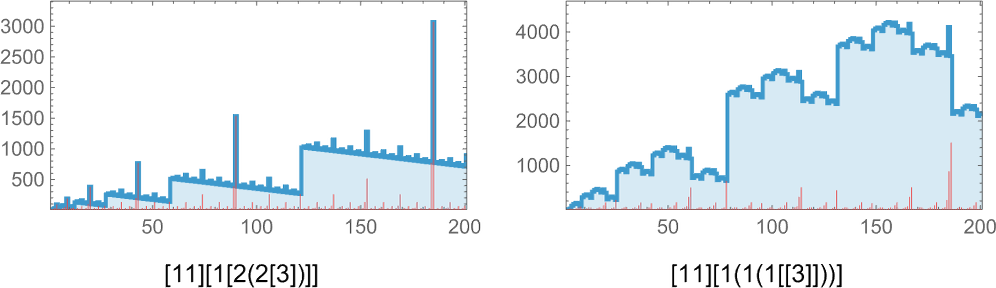
And then there’s nested structure, but superimposed on ![]() growth:
growth:

At size 11, there are 63,782,411 possible lambdas. Most of the behavior one sees looks very much as before. But there are some surprises. One of them is:
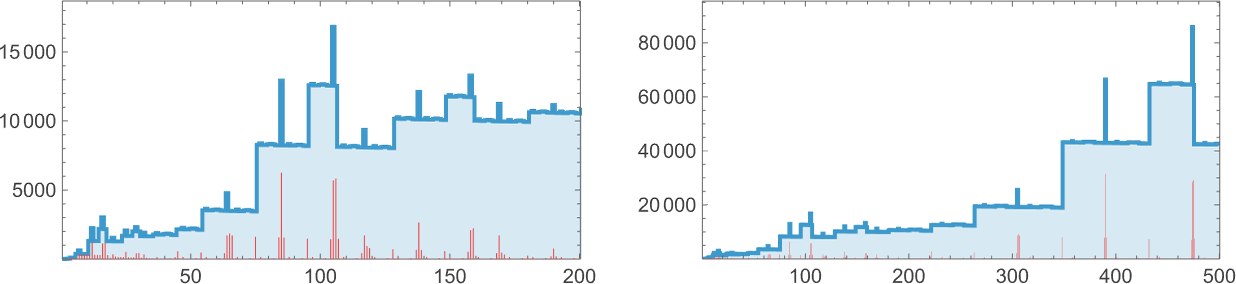
And another is:

And, yes, there doesn’t seem to be any overall regularity here, and nor does any show up in the detailed sequence of lambdas produced:

So far as I can tell, like so many other simple computational systems—from rule 30 on—the fairly simple lambda
just keeps generating unpredictable behavior forever.
How do we know whether the evaluation chain for a particular lambda will terminate? Well, we can just run it for a certain number of steps and see if it terminates by then. And perhaps by that point we will see obvious periodic or nested behavior that will make it clear that it won’t ever terminate. But in general we have no way to know how long we might have to run it to be able to determine whether it terminates or not.
It’s a very typical example of the computational irreducibility that occurs throughout the world of even simple computational systems. And in general it leads us to say that the problem of whether a given lambda evaluation will terminate must be considered undecidable, in the sense that there’s no computation of bounded length that can guarantee to answer the question.
But what happens in practice? Well, we’ve seen above that at least for sufficiently small lambdas it’s not too hard to resolve the question of termination. But already at size 10 there are issues. Take for example:
The first 1000 steps of evaluation lead to lambdas with a sequence of sizes that seem like they’re basically just uniformly increasing:

After 10,000 steps it’s the same story—with the size growing roughly like t/3:

But if we look at the structure of the actual underlying lambdas—even for just 200 steps—we see that there’s a “dead region” that’s beginning to build up:

Continuing to 500 steps, the dead region continues to grow more or less linearly:

“Detrending” the sequences of sizes by subtracting t/3 we get:

There’s definite regularity here, which suggests that we might actually be able to identify a “pocket of computational reducibility” in this particular case—and be able to work out what will happen without having to explicitly run each step.
And, yes, in fact that’s true. Let’s look again at the form of the lambda we’re dealing with:
The second part turns out to be the (“Church numeral”) representation we used for the number 2. Calling this ![]() the whole lambda evaluates according to:
the whole lambda evaluates according to:
Normally you might think of doing things like arithmetic operations on integers. But here we’re seeing something different: we’re seeing integers in effect applied to integers. So what, for example, does
or
evaluate to? Repeatedly doing beta reduction gives:
Or, in other words ![]() gives
gives ![]() . Here are some other examples:
. Here are some other examples:

And in general:
So now we can “decode” our original lambda. Since
evaluates to
this means that
is just:
Or, in other words, despite how it might have looked at first, the evaluation of our original lambda will eventually terminate, giving a lambda of size 65539—and it’ll take about 200,000 steps to do this. (Curiously, this whole setup is extremely similar to something I studied about 30 years ago in connection with combinator-like systems of the form e[x_][y_]![]() x[x[y]].)
x[x[y]].)
It’s somewhat remarkable how long it took our simple lambda to terminate. And actually, given what we’ve seen here, it’s straightforward to construct lambdas that will terminate, but will take even longer to do so. So, for example
evaluates to the n-fold “tetration”
and takes about that many steps to do so.
In the next section we’ll see how to set up lambdas that can compute not just tetration, but the Ackermann function, and any level of hyperoperation, as defined recursively by
(where h[1] is Plus, h[2] is Times, h[3] is Power, h[4] is tetration, etc.).
OK, so there are lambdas (and actually even rather simple ones) whose evaluation terminates, but only after a number of steps that has to be described with hyperoperations. But what about lambdas that don’t terminate at all? We can’t explicitly trace what the lambda does over the course of an infinite number of steps. So how can we be sure that a lambda won’t terminate?
Well, we have to construct a proof. Sometimes that’s pretty straightforward because we can easily identify that something fundamentally simple is going on inside the lambda. Consider for example:
The successive steps in its evaluation are (with the elements involved in each beta reduction highlighted):
It’s very obvious what’s going on here, and that it will continue forever. But if we wanted to, we could construct a formal proof of what’s going to happen—say using mathematical induction to relate one step to the next.
And indeed whenever we can identify a (“stem-cell-like”) core “generator” that repeats, we can expect to be able to use induction to prove that there won’t be termination. There are also plenty of other cases that we’ve seen in which we can tell there’s enough regularity—say in the pattern of successive lambdas—that it’s “visually obvious” there won’t be termination. And though there will often be many details to wrestle with, one can expect a straightforward path in such cases to a formal proof based on mathematical induction.
In practice one reason “visual obviousness” can sometimes be difficult to identify is that lambdas can grow too fast to be consistently visualized. The basic source of such rapid growth is that beta reduction ends up repeatedly replicating increasingly large subexpressions. If these replications in some sense form a simple tree, then one can again expect to do induction-based proofs (typically based on various kinds of tree traversals). But things can get more complicated if one starts ascending the hierarchy of hyperoperations, as we know lambdas can. And for example, one can end up with situations where every leaf of every tree is spawning a new tree.
At the outset, it’s certainly not self-evident that the process of induction would be a valid way to construct a proof of a “statement about infinity” (such as that a particular lambda won’t ever terminate, even after an infinite number of steps). But induction has a long history of use in mathematics, and for more than a century has been enshrined as an axiom in Peano arithmetic—the axiom system that’s essentially universally used (at least in principle) in basic mathematics. Induction in a sense says that if you always have a way to take a next step in a sequence (say on a number line of integers), then you’ll be able to go even infinitely far in that sequence. But what if what you’re dealing with can’t readily be “unrolled” into a simple (integer-like) sequence? For example, what if you’re dealing with trees that are growing new trees everywhere? Well, then ordinary induction won’t be enough to “get you to all the leaves”.
But in set theory (which is typically the ultimate axiom system in principle used for current mathematics) there are axioms that go beyond ordinary induction, and that allow the concept of transfinite induction. And with transfinite induction (which can “walk through” all possible ordered sets) one can “reach the leaves” in a “trees always beget trees” system.
So what this means is that while the nontermination of a sufficiently fast-growing lambda may not be something that can be proved in Peano arithmetic (i.e. with ordinary induction) it’s still possible that it’ll be provable in set theory. Inevitably, though, even set theory will be limited, and there’ll be lambdas whose nontermination it can’t prove, and for which one will have to introduce new axioms to be able to produce a proof.
But can we explicitly see lambdas that have these issues? I wouldn’t be surprised if some of the ones we’ve already considered here might actually be examples. But that will most likely be a very difficult thing to prove. And an easier (but still difficult) approach is to explicitly construct, say, a family of lambdas where within Peano arithmetic there can be no proof that they all terminate.
Consider the slightly complicated definitions:
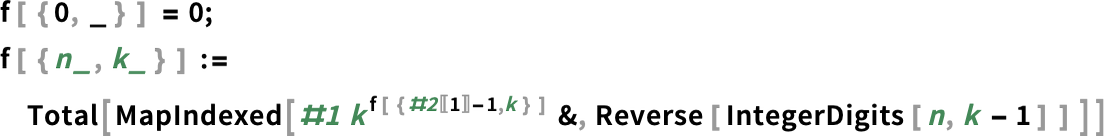
The g[n] are the so-called Goodstein sequences for which it’s known that the statement that they always reach 0 is one that can’t be proved purely using ordinary induction, i.e. in Peano arithmetic.
Well, here’s a lambda—that’s even comparatively simple—that has been constructed to compute the lengths of the Goodstein sequences:
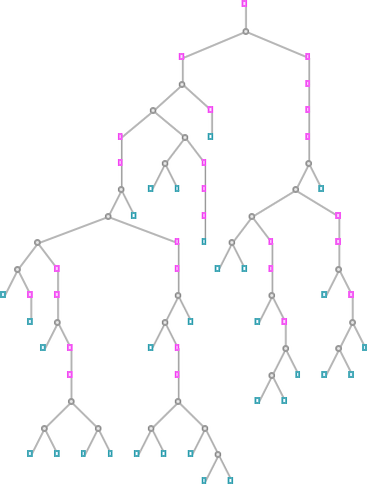
Feed in a representation of an integer n, and this lambda will compute a representation of the length of the corresponding sequence g[n] (i.e. how many terms are needed to reach 0). And this length will be finite if (and only if) the evaluation of the lambda terminates. So, in other words, the statement that all lambda evaluations of this kind terminate is equivalent to the statement that all Goodstein sequences eventually reach 0.
But what actually happens if we evaluate lambdas of this kind? Here are the results for the first few values of ![]() :
:
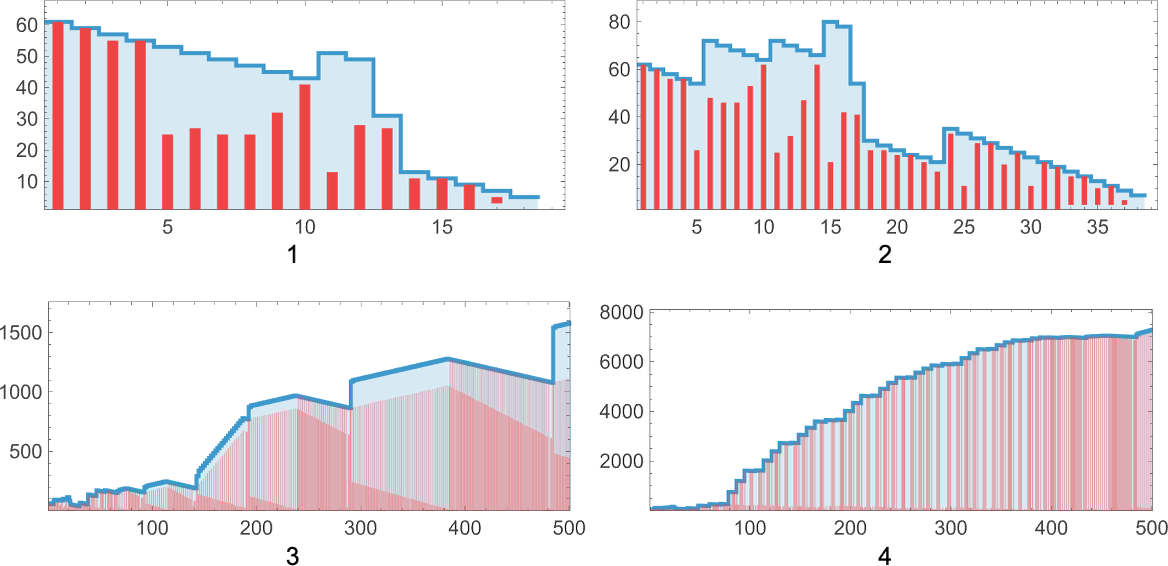
For n = 1, the process terminates in 18 steps with final result λ[λ[2[2[1]]]]—our representation for the integer 2—reflecting the fact that g[1] = {1, 0}. For n = 2, after 38 steps we get the integer 4, reflecting the fact that g[2] = {2, 2, 1, 0}. For n = 3 many more steps are needed, but eventually the result is 6 (reflecting the fact that g[3] = {3, 3, 3, 2, 1, 0}). But what about n = 4? Well, it’s known that the process must eventually terminate in this case too. But it must take a very long time—since the final result is known to be ![]() . And if we keep going, the sizes—and corresponding times—rapidly get still much, much larger.
. And if we keep going, the sizes—and corresponding times—rapidly get still much, much larger.
This certainly isn’t the only way to “escape provability by Peano arithmetic”, but it’s an example of what this can look like.
We should remember that in general whether the evaluation of a lambda ever terminates is a question that’s fundamentally undecidable—in the sense that no finite computation whatsoever can guarantee to answer it. But the question of proving, say, that the evaluation of a particular lambda doesn’t terminate is something different. If the lambda “wasn’t generating much novelty” in its infinite lifetime (say it was just behaving in a repetitive way) then we’d be able to give a fairly simple proof of its nontermination. But the more fundamentally diverse what the lambda does, the more complicated the proof will be. And the point is that—essentially as a result of computational irreducibility—there must be lambdas whose behavior is arbitrarily complex, and diverse. But in some sense any given finite axiom system can only be expected to capture a certain “level of diversity” and therefore be able to prove nontermination only for a certain set of lambdas.
To be slightly more concrete, we can imagine a construction that will lead us to a lambda whose termination can’t be proved within a given axiom system. It starts from the fact that the computation universality of lambdas implies that any computation can be encoded as the evaluation of some lambda. So in particular there’s a lambda that systematically generates statements in the language of a given axiom system, determining whether each of those statements is a theorem in that axiom system. And we can then set it up so that if ever an inconsistency is found—in the sense that both a theorem and its negation appear—then the process will stop. In other words, the evaluation of the lambda is in a sense systematically looking for inconsistencies in the axiom system, terminating if it ever finds one.
So this means that proving the evaluation of the lambda will never terminate is equivalent to proving that the axiom system is consistent. But it’s a fundamental fact that a given axiom system can never prove its own consistency; it takes a more powerful axiom system to do that. So this means that we’ll never be able to prove that the evaluation of the lambda we’ve set up terminates—at least from within the axiom system that it’s based on.
In effect what’s happened is that we’ve managed to make our lambda in its infinite lifetime scan through everything our axiom system can do, with the result that the axiom system can’t “go further” and say anything “bigger” about what the lambda does. It’s a consequence of the computation universality of lambdas that it’s possible to package up the whole “metamathematics” of our axiom system into the (infinite) behavior of a single lambda. But the result is that for any given axiom system we can in principle produce a lambda where we know that the nontermination of that lambda is unprovable within that axiom system.
Of course, if we extend our axiom system to have the additional axiom “this particular lambda never terminates” then we’ll trivially be able to prove nontermination. But the underlying computation universality of lambdas implies (in an analog of Gödel’s theorem) that no finite collection of axioms can ever successfully let us get finite proofs for all possible lambdas.
And, yes, while the construction we’ve outlined gives us a particular way to come up with lambdas that “escape” a given axiom system, those certainly won’t be the only lambdas that can do it. What will be the smallest lambda whose nontermination is unprovable in, say, Peano arithmetic? The example we gave above based on Goodstein sequences is already quite small. But there are no doubt still much smaller examples. Though in general there’s no upper bound on how difficult it might be to prove that a particular lambda is indeed an example.
If we scan through all possible lambdas, it’s inevitable that we’ll eventually find a lambda that can “escape” from any possible axiom system. And from experience in the computational universe, we can expect that even for quite small lambdas there’ll be rapid acceleration in the size and power of axiom systems needed to “rein them in”. Yes, in principle we can just add a custom axiom to handle any given lambda, but the point is that we can expect that there’ll quickly be in a sense “arbitrarily small leverage”: each axiom added will cover only a vanishingly small fraction of the lambdas we reach.
So far, we’ve discussed the evaluation of “lambdas on their own”. But given a particular lambda, we can always apply it to “input”, and see “what it computes”. Of course, the input itself is just another lambda, so a “lambda applied to input” is just a “lambda applied to a lambda”, which is itself a lambda. And so we’re basically back to looking at “lambdas on their own”.
But what if the input we give is something “interpretable”? Say a lambda corresponding to an integer in the representation we used above. A lambda applied to such a thing will—assuming it terminates—inevitably just give another lambda. And most of the time that resulting lambda won’t be “interpretable”. But sometimes it can be.
Consider for example:
Here’s what happens if we apply this lambda to a sequence of integers represented as lambdas:


In other words, this lambda can be interpreted as implementing a numerical function from integers to integers—in this case the function:
So what kinds of such numerical functions can lambdas represent? Insofar as lambdas are capable of universal computation, they must in the end be capable of representing any integer function. But the necessary lambda could be very large.
Early on above, we saw a constructed representation for the factorial function as a lambda:
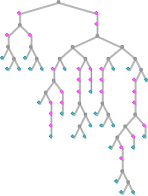
We also know that if we take the (“Church numeral”) lambda that represents an integer m and apply it to the lambda that represents n, we get the lambda representing nm. It’s then straightforward to construct a lambda that represents any function that can be obtained as a composition of powers:

And one can readily go on to get functions based on tetration and higher hyperoperations. For example
gives a diagonal of the Ackermann function whose successive terms are:
But what about “lambdas in the wild”? How often will they be “numerically interpretable”? And what kinds of functions will they represent? Among size-5 lambdas, for example, 10 out of 82—or about 12%—are “interpretable”, and represent the functions 0, 1, n and n2. Among size-10 lambdas the fraction that are “interpretable” falls to about 4%, and the frequency with which different functions occur is:
Looking at lambdas of successively greater size, here are some notable “firsts” of where functions appear:

And, yes, we can think of the size of the minimal lambda that gives a particular function to be the “algorithmic information content” of that function with respect to lambdas.
Needless to say, there are some other surprises. Like , which gives 0 when fed any integer as input, but takes a superexponentially increasing number of steps to do so:
, which gives 0 when fed any integer as input, but takes a superexponentially increasing number of steps to do so:
We’ve been discussing what “numerical” functions can be computed by what lambdas. But another question we can ask is how much time (i.e. how many beta reductions) such computations will take—or how much “space” they’ll need for intermediate expressions. And indeed, even if the outputs are the same, different lambdas can take different computational approaches and different computational resources to reach those outputs. So, for example, among size-8 lambdas, there are 41 that compute the function n2. And here are the sizes of intermediate expressions (all plotted on the same scale) generated by running these lambdas for the case n = 10:

The pictures suggest that these various lambdas have a variety of different approaches to computing n2. And some of these approaches take more “memory” (i.e. size of intermediate lambdas) than others. And in addition some take more time than others.
For this particular set of lambdas, the time required always grows essentially just linearly with n, though at several different possible rates:
But in other cases, different behavior is observed, including some very long “run times”. And indeed, in general, one can imagine building up a whole computational complexity theory for lambdas, starting with these kinds of empirical, ruliological investigations.
Everything we’ve discussed here so far is for functions with single arguments. But we can also look at functions that have multiple arguments, which can be fed to lambdas in “curried” form: f [x][y], etc. And with this setup, , for example, gives x y while
, for example, gives x y while gives x y3.
gives x y3.
Let’s say you’re evaluating a lambda expression like:
You want to do a beta reduction. But which one? For this expression, there are 3 possible places where a beta reduction can be done, all giving different results:
In everything we’ve done so far, we’ve always assumed that we use the “first” beta reduction at each step (we’ll discuss what we mean by “first” in a moment). But in general we can look at all possible “paths of evaluation”—and form a multiway graph from them (the double edge reflects the fact that two different beta reductions happen to both yield the same result):
Our standard evaluation path in this case is then:
And we get this path by picking at each step the “leftmost outermost” possible beta reduction, i.e. the one that involves the “highest” relevant λ in the expression tree (and the leftmost one if there’s a choice):
But in the multiway graph above it’s clear we could have picked any path, and still ended up at the same final result. And indeed it’s a general property of lambdas (the so-called confluence or Church–Rosser property) that all evaluations of a given lambda that terminate will terminate with the same result.
By the way, here’s what the multiway graph looks like with the lambdas rendered in tree form:
At size 5, all lambdas give trivial multiway graphs, that involve no branching, as in:
At size 6, there starts to be branching—and merging:
And something else happens too: the “looping lambda” λ[1[1]][λ[1[1]]] gives a multiway graph that is a loop:

At size 7 many distinct topologies of multiway graphs start to appear. Most always lead to termination:
(The largest of these multiway graphs is associated with λ[1[1]][λ[λ[2][1]]] and has 12 nodes.)
Then there are cases that loop:
And finally there is
where something new happens: the multiway graph has many distinct branches. After 5 steps it is

where the size of each node indicates the size of the lambda it represents, and the pink nodes indicate lambdas that can be further beta reduced. After just one more step the multiway graph becomes
or, after another step, in a hyperbolic embedding:

In this particular case, no branch ever terminates, and the total size of the multiway system on successive steps is:
With size-8 lambdas, the terminating multiway graphs can be larger (the first case has 124 nodes):
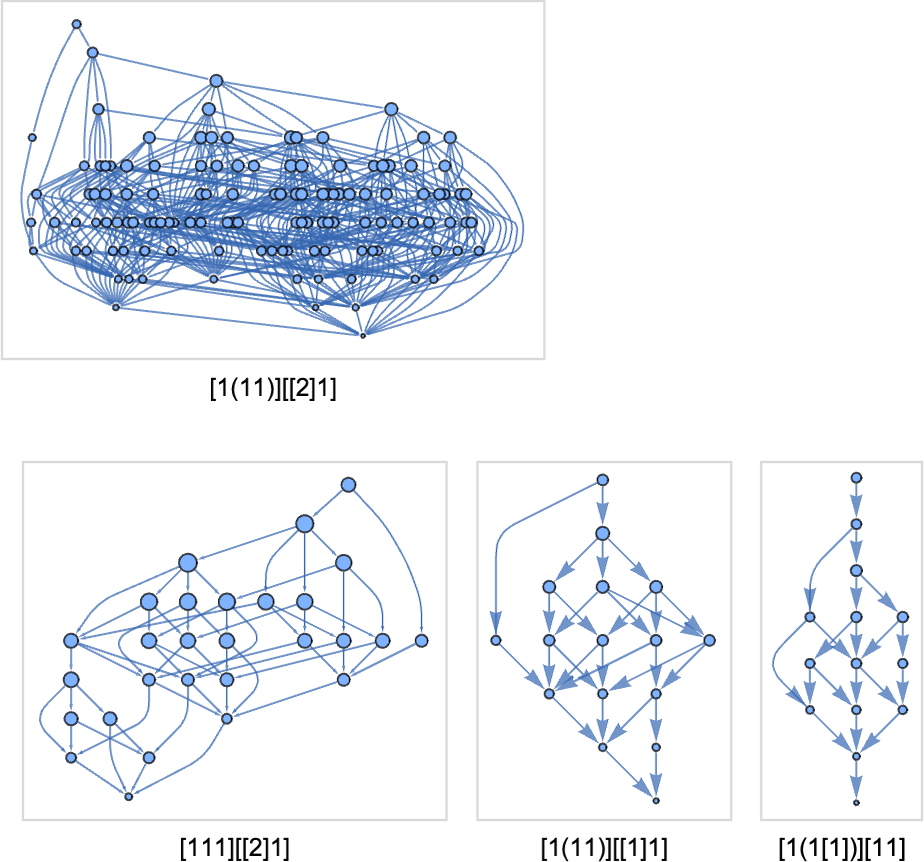
And there are all sorts of new topologies for nonterminating cases, such as:

These graphs are what one gets by doing 5 successive beta reductions. The ones that end in loops won’t change if we do more reductions. But the ones with nodes indicated in pink will. In most cases one ends up with a progressively increasing number of reductions that can be done (often exponential, but here just 2t – 1 at step t):

Meanwhile, sometimes, the number of “unresolved reductions” just remains constant:

We know that if there’s a fixed point to beta reductions, it’s always unique. But can there be both a unique fixed point, and branches that continue forever? It turns out that there can. And the first lambda for which this happens is:
With our standard evaluation method, this lambda terminates in 5 steps at λ[1]. But there are other paths that can be followed, that don’t terminate (as indicted by pink nodes at the end):
And indeed on step t, the number of such paths is given by a Fibonacci-like recurrence, growing asymptotically ![]() .
.
With size-9 lambdas there’s a much simpler case where the termination/nontermination phenomenon occurs
where now at each step there’s just a single nonterminating path:

There’s another lambda where there’s alternation between one and two nonterminating paths:

And another where there are asymptotically always exactly 5 nonterminating paths:

OK, so some lambdas have very “bushy” (or infinite) multiway graphs, and some don’t. How does this correlate with the lifetimes we obtain for these lambdas through our standard evaluation process?
Here’s a plot of the size of the multiway graph versus lifetime for all finite-lifetime size-8 lambdas:
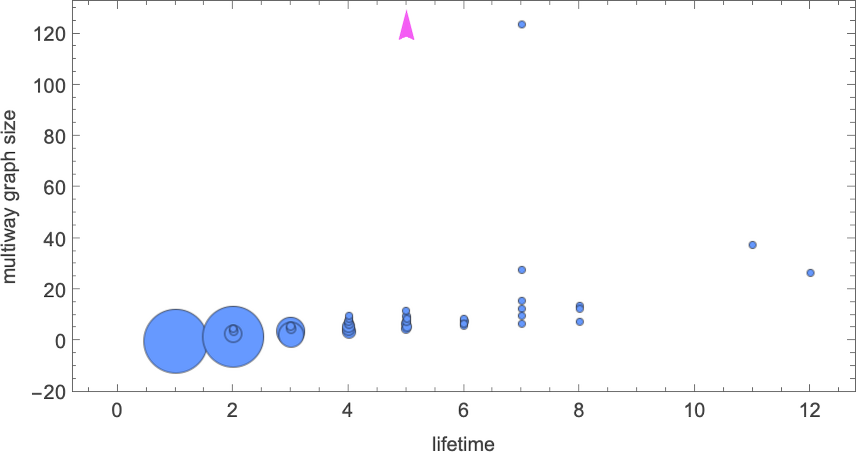
In all but the one case discussed above (and indicated here with a red arrow) the multiway graphs are of finite size—and we see some correlation between their size and the lifetime obtained with our standard evaluation process. Although it’s worth noting that even the lambda with the longest standard-evaluation lifetime (12) still has a fairly modest (27-node) multiway graph
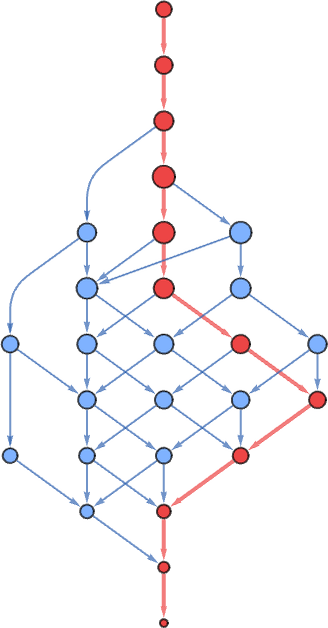
while the largest (finite) multiway graph (with 124 nodes) occurs for a lambda with standard-evaluation lifetime 7.
At size 9, here are the multiway graphs for the 10 lambdas with the longest standard-evaluation lifetimes, computed to 5 steps:
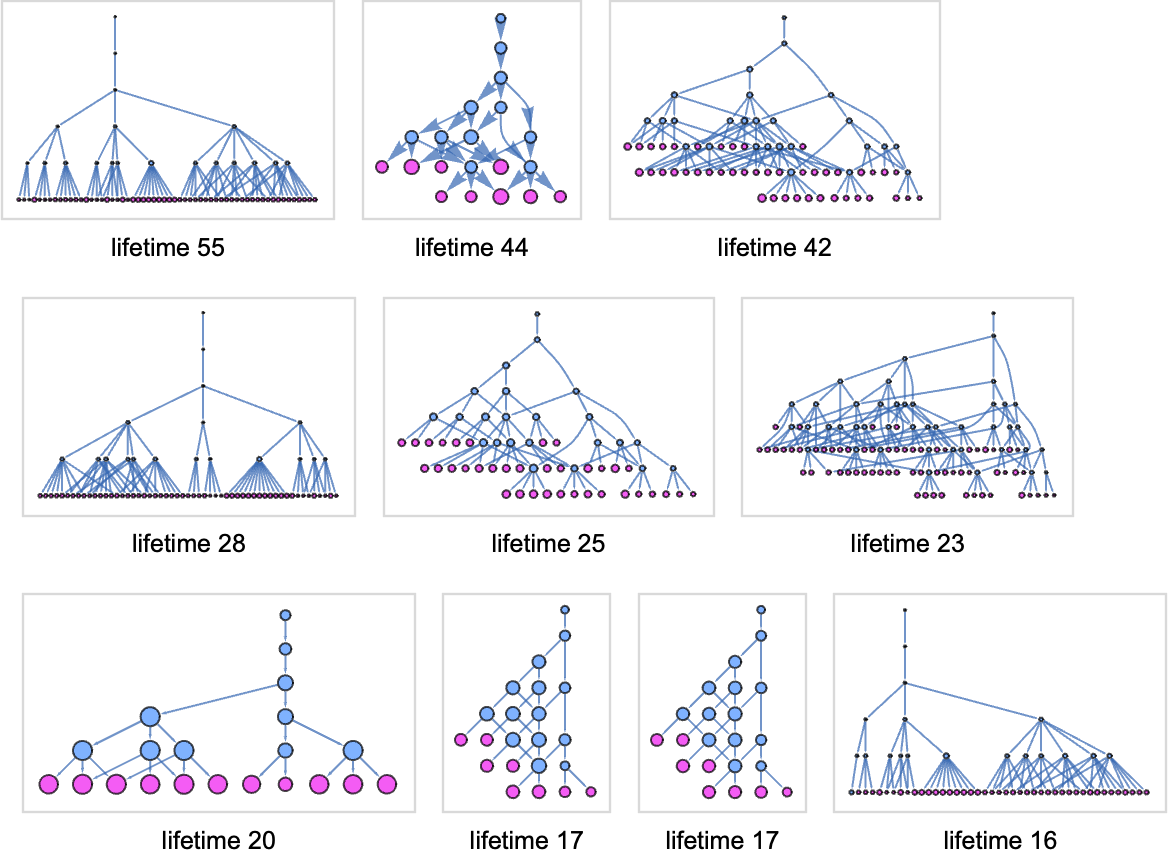
In the standard-evaluation lifetime-17 cases the multiway graph is finite:
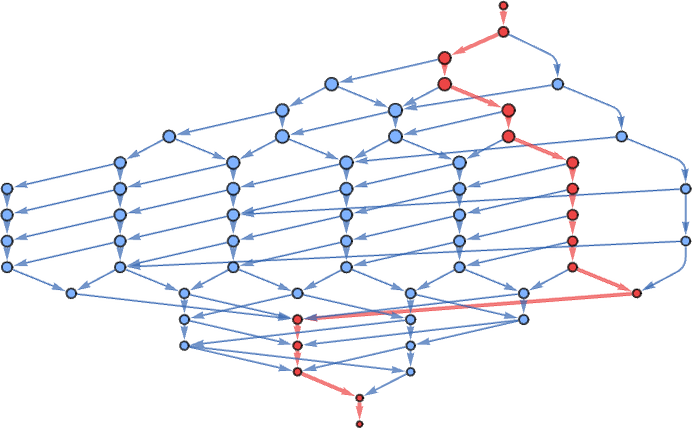
But in all the other cases shown, the graph is presumably infinite. And for example, in the lifetime-55 case, the number of nodes at step t in the multiway graph grows like:
But somehow, among all these different paths, we know that there’s at least one that terminates—at least after 55 steps, to give λ[1].
The multiway graph shows us all possible sequences of beta reductions for a lambda. Our “standard evaluation process” picks one particular sequence—by having a certain strategy for choosing at each step what beta reduction to do. But what if we were to use a different strategy?
As a first example, consider:
For this lambda, there turn out to be 4 possible positions at which beta reductions can be done (where the positions are specified here using Wolfram Language conventions):
Our standard evaluation strategy does the beta reduction that’s listed first here. But how exactly does it determine that that’s the reduction it should do? Well, it looks at the lists of 0’s and 1’s that specify the positions of each of the possible reductions in the lambda expression tree. Then it picks the one with the shortest position list, sorting position lists lexicographically if there’s a tie.
In terms of the structure of the tree, this corresponds to picking the leftmost outermost beta reduction, i.e. the one that in our rendering of the tree is “highest and furthest to the left”:
So what are some other strategies we could use? One way we can specify a strategy is by giving an algorithm that picks one list out of any collection of lists of 0’s and 1’s. (For now we’ll consider only “sequential strategies”, that pick out a single position list—i.e. a single reduction—at a time.) But another way to specify a strategy is to define an ordering on the expression tree, then to say that the beta reduction we’ll do is the one we reach first if we traverse the tree in that order. And so, for example, our leftmost outermost strategy is associated with a breadth-first traversal of the tree. Another evaluation strategy is leftmost innermost, which is associated with a depth-first traversal of the tree, and a purely lexicographic ordering, independent of length, of all tree positions of beta reductions.
In the Wolfram Language, the option TreeTraversalOrder gives detailed parametrizations of possible traversal orders for use in functions like TreeMap—and each of these orders can be used to define an evaluation strategy for lambdas. The standard ReplaceAll (/.) operation applied to expression trees in the Wolfram Language also defines an evaluation strategy—which turns out to be exactly our standard outermost leftmost one. Meanwhile, using standard Wolfram Language evaluation after giving an assignment λ[x_][y_]:=… yields the leftmost innermost evaluation strategy (since at every level the head λ[…] is evaluated before the argument). If the λ had a Hold attribute, however, then we’ll instead get what we can call “applicative” order, in which the arguments are evaluated before the body. And, yes, this whole setup with possible evaluation strategies is effectively identical to what I discussed at some length for combinators a few years ago.
OK, so what happens with different strategies? Here are examples of the evaluation chains generated in various different cases:

Each of these corresponds to following a different path in the multiway graph:
And each, in effect, corresponds to a different way to reach the final result:
Plotting the sizes of lambdas obtained at each step, we see that different strategies have different profiles—notably in this case with the standard strategy taking more steps to reach the final result than, for example, depth first:
OK, but so what exactly do these strategies mean? In terms of Wolfram Language function TreeTraversalOrder they are (“applicative” involves dependence on whether an element is a λ or a •, and works slightly differently):

In terms of tree positions, these correspond to the following orderings

which correspond to these paths through nodes of a tree:
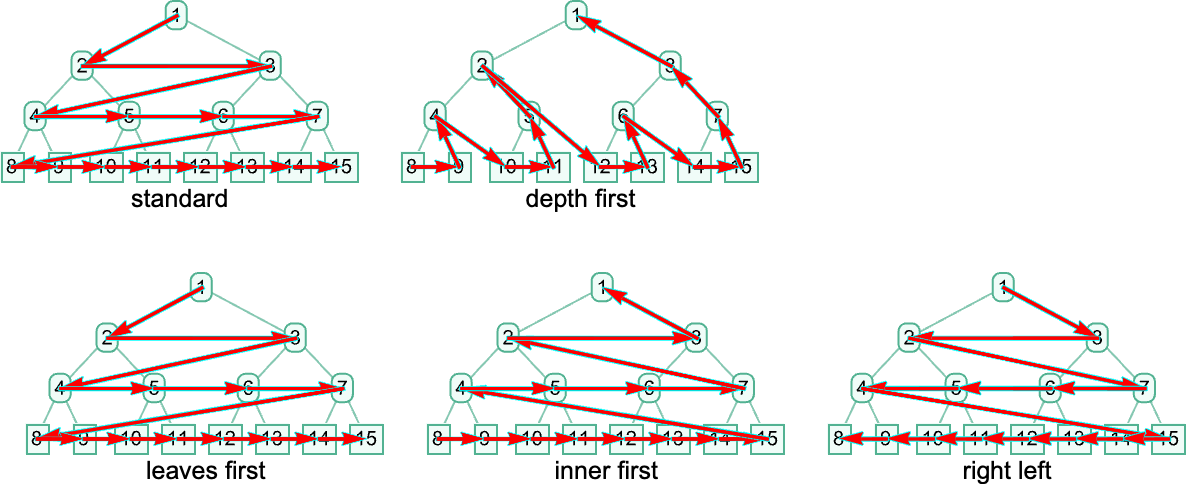
As we mentioned much earlier, it is a general feature of lambdas that if the evaluation of a particular lambda terminates, then the result obtained must always be the same—independent of the evaluation strategy used. In other words, if there are terminating paths in the multiway graph, they must all converge to the same fixed point. Some paths may be shorter than others, representing the fact that some evaluation strategies may be more efficient than others. We saw one example of this above, but the differences can be much more dramatic. For example,  takes 74 steps to terminate with our standard evaluation strategy, but only 10 with depth first:
takes 74 steps to terminate with our standard evaluation strategy, but only 10 with depth first:
And indeed it’s fairly common to see cases where standard evaluation and depth first produce very different behavior; sometimes one is more efficient, sometimes it’s the other. But despite differences in “how one gets there”, the final fixed-point results are inevitably always the same.
But what happens if only some paths in the multiway graph terminate? That’s not something that happens with any lambdas up to size 8. But at size 9, for example,  terminates with standard evaluation but not with depth first:
terminates with standard evaluation but not with depth first:
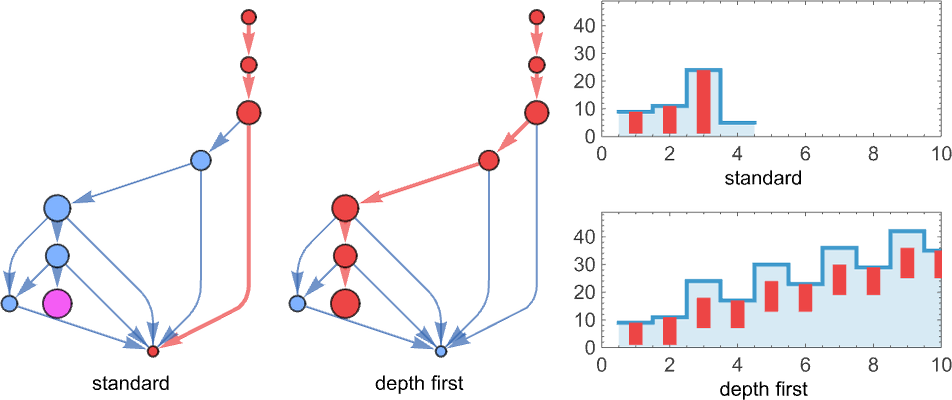
And an even simpler example is  :
:
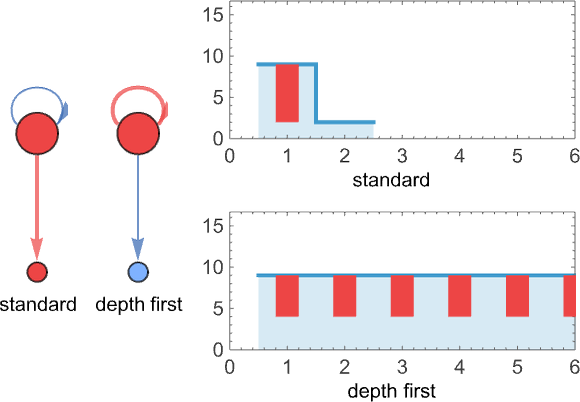
In both these cases, standard evaluation leads to termination, but depth-first evaluation does not. And in fact it’s a general result that if termination is ever possible for a particular lambda, then our standard (“leftmost outermost”) evaluation strategy will successfully achieve it.
But what if termination is never possible? Different evaluation strategies can lead to different behavior. For example,  can get stuck in a loop of either period 2 or period 1:
can get stuck in a loop of either period 2 or period 1:
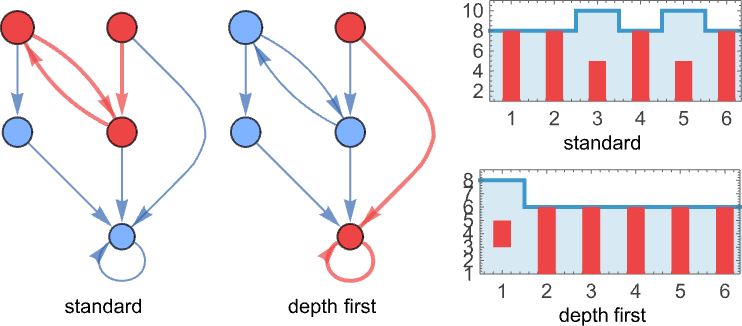
It’s also possible for one strategy to give lambdas that grow forever, and another to give lambdas that are (as in this 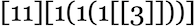 case), say, periodic in size—in effect showing two different ways of not terminating:
case), say, periodic in size—in effect showing two different ways of not terminating:
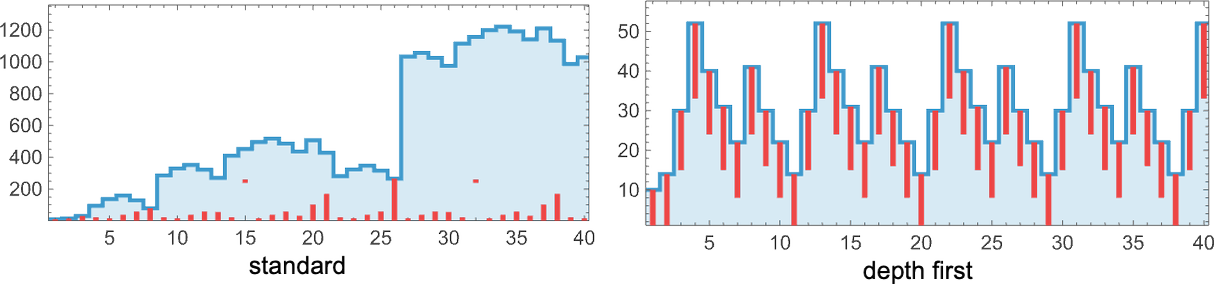
But what if one has a whole collection of lambdas? What generically happens? Within every multiway graph there can be a fixed point, some number of loops and some (tree-like) unbounded growth. Every strategy defines a path in the multiway graph—which can potentially lead to any of these possible outcomes. It’s fairly typical to see one type of outcome be much more likely than others—and for it to require some kind of “special tuning” to achieve a different type of outcome.
For this case
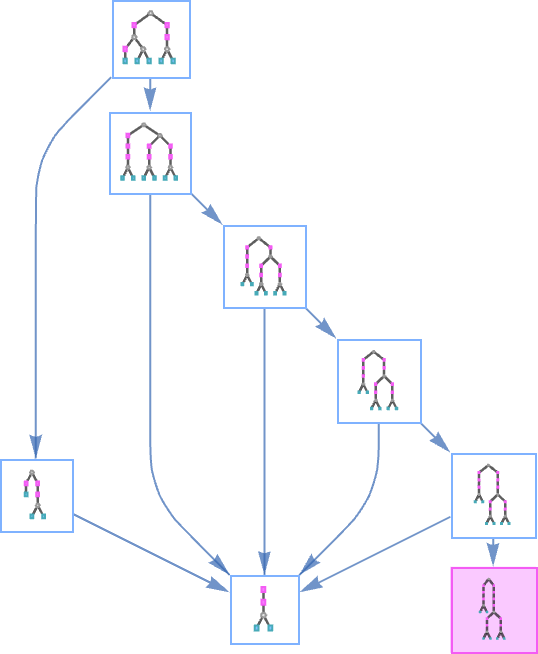
almost all evaluation strategies lead to termination—except the particular strategy based on what we might call “tree layout order”:
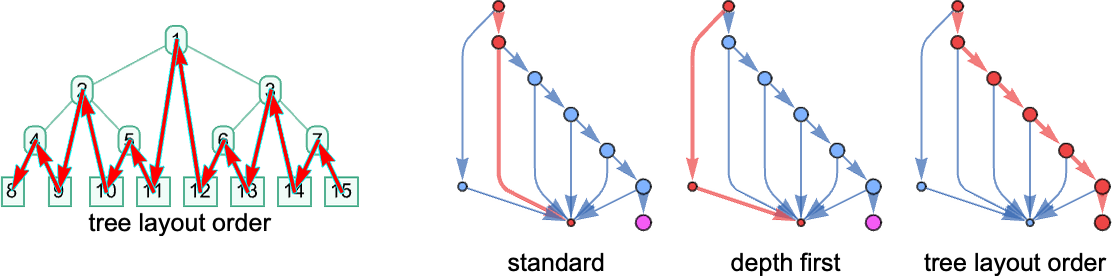
So what happens if we use a strategy where at each step we just pick between different possible beta reductions at random, with equal probability? Here are some examples for the [1(11)][[2(211)]] lambda we saw above, that takes 74 steps to terminate with our standard evaluation strategy:
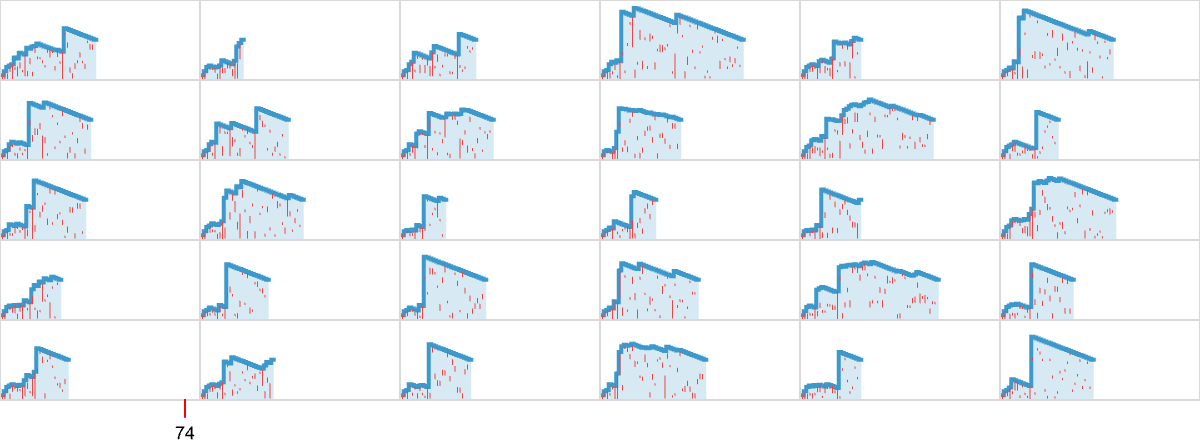
There’s quite a diversity in the shapes of curves generated. But it’s notable that no nonterminating cases are seen—and that termination tends to occur considerably more quickly than with standard evaluation. Indeed, the distribution of termination times only just reaches the value 74 seen in the standard evaluation case:
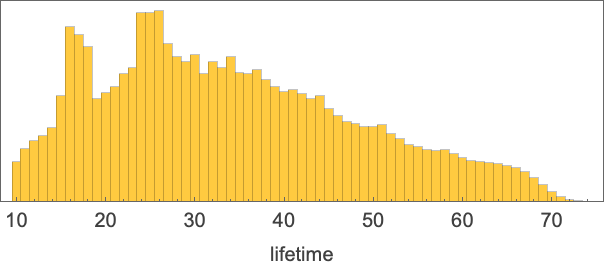
For lambdas whose evaluation always terminates, we can think of the sequence of sizes of expressions generated in the course of their evaluation as being “pinned at both ends”. When the evaluation doesn’t terminate, the sequences of sizes can be wilder, as in these [11][1(1(1[[3]]))] cases:

Consider the lambdas:
They each have a different form. But they all evaluate to the same thing: λ[1]. And particularly if we’re thinking about lambdas in a mathematically oriented way this means we can think of all these lambdas as somehow “representing the same thing”, and therefore we can consider them “equivalent”.
Out of all 18 lambdas up to size 4, these three are actually the only ones that are equivalent in this sense. So that means there are 15 “evaluation inequivalent” lambdas up to size 4.
Up to size 5, there are a total of 100 forms of lambdas—which evolve to 68 distinct final results—and there are 4 multi-lambda equivalence classes
which we can summarize graphically as:
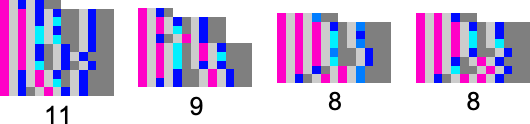
Up to size 6, there are a total of 679 forms of lambdas—which evolve to 392 distinct final states (along with one “looping lambda”)—and there are 16 multi-lambda equivalence classes:
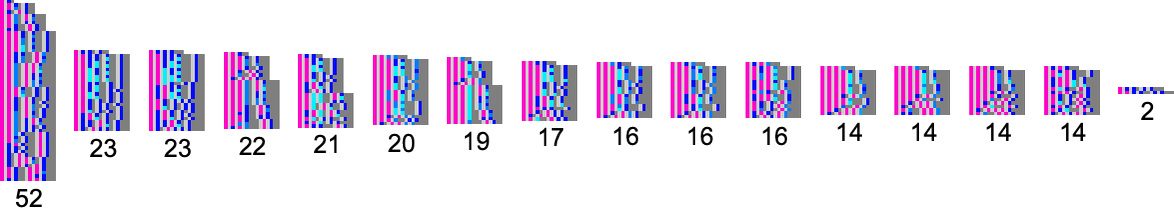
If we look only at lambdas whose evaluation terminates then we have the following:

For large sizes, the ratio conceivably goes more or less exponentially to a fixed limiting value around 1/4.
But this is only for lambdas that terminate. So what can we say about equivalences between lambdas that don’t terminate? Well, it depends what we mean by “equivalence”. One definition might be that two lambdas are equivalent if somewhere in their evolution they generate identical lambda expressions. Or, in other words, there is some overlap in their multiway graphs.
If we look up to size 7, there are 8 lambdas that don’t terminate, and there’s a single—rather simple—correspondence between their multiway systems:
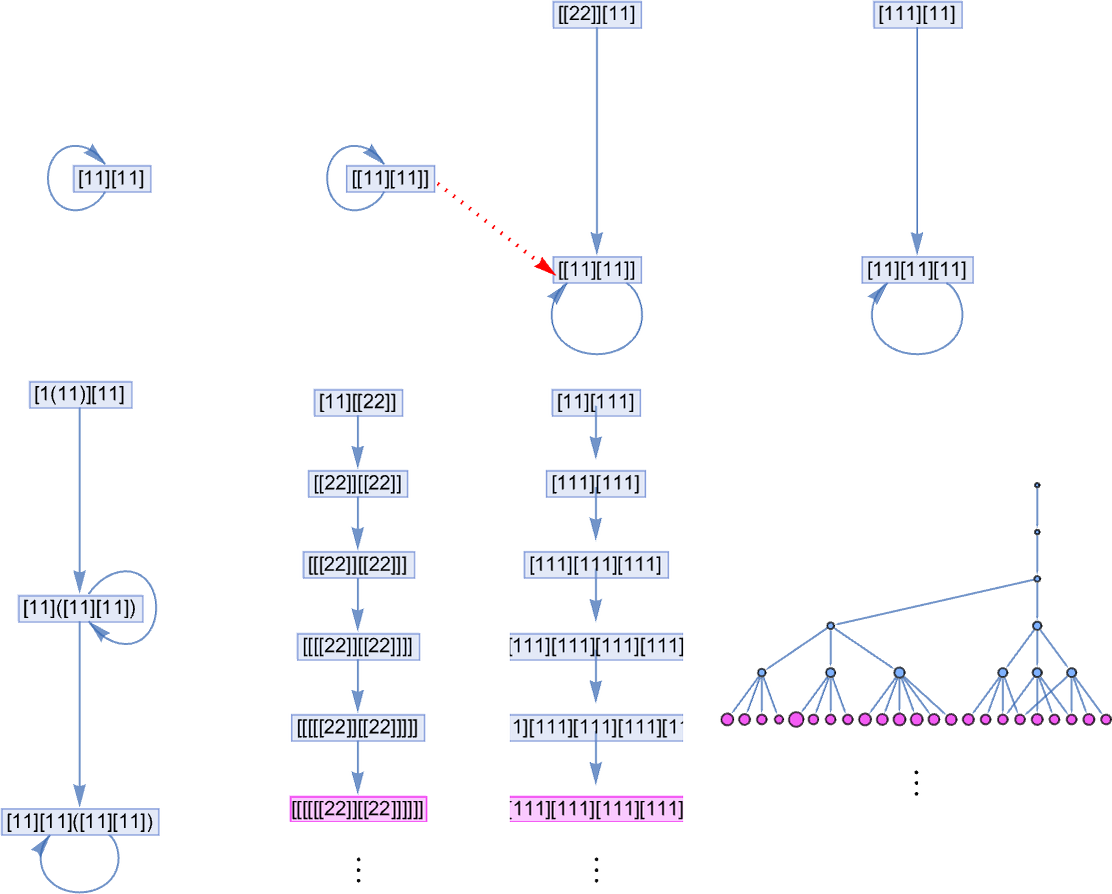
Up to size 8, there are 89 lambdas whose evaluation doesn’t terminate. And among these, there are many correspondences. A simple example is:

More elaborate examples include
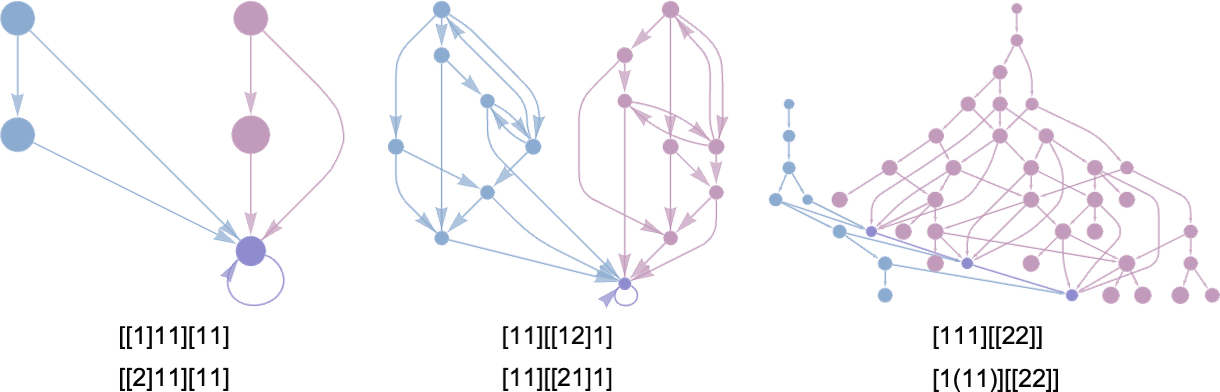
where now we are showing the combined multiway graphs for pairs of lambdas. In the first two cases, the overlap is at a looping lambda; in the third it is at a series of lambda expressions.
If we look at all 89 nonterminating lambdas, this shows which are the 434 overlapping pairs:

There are several subtleties here. First, whether two lambdas are “seen to be equivalent” can depend on the evaluation strategy one’s using. For example, a lambda could terminate for one strategy, but can “miss the fixed point” with another strategy that fails to terminate.
In addition, even if the multiway graphs for two lambdas overlap, there’s no guarantee that that overlap will be “found” with any given evaluation strategy.
And, finally, as so often, there’s an issue of undecidability. Even if a lambda is going to terminate, it can take an arbitrarily long time to do so. And, worse, if one progressively generates the multiway graphs for two lambdas, it can be arbitrarily difficult to see if they overlap. Determining a single evaluation path for a lambda can be computationally irreducible; determining these kinds of overlaps can be multicomputationally irreducible.
We can think of every beta reduction in the evaluation of a lambda as an “event” in which certain input is transformed to certain output. If the input to one event V relies on output from another event U, then we can say that V is causally dependent on U. Or, in other words, the event V can only happen if U happened first.
If we consider a lambda evaluation that involves a chain of many beta reductions, we can then imagine building up a whole “causal graph” of dependencies between beta reduction events.
As a simple example, consider this evaluation chain, where we’ve explicitly shown the beta reduction events, and (for clarity in this simple case) we’ve also avoided renaming the variables that appear:
The blue edges here show how one lambda transforms to another—as a result of an event. The dark red edges show the causal relations between events; each of them can be thought of as being associated with a subexpression that is the “carrier of causality” from one event to another.
Keeping only events and causal edges, the causal graph for this evolution is then:
If we follow a sequence of causal edges we get a “timelike” chain of events that must occur in order. But “transverse” to that we can have (in the language of posets) an “antichain” consisting of what we can think of as “spacelike separated” events that can occur in parallel. In this case the first event (i.e. the first beta reduction) leads to the expression
in which there are two reductions that can be done: for λ[b,…] and for the first λ[c,…]. But these reductions are completely independent of each other; they can be thought of as “spacelike separated”. In our standard evaluation scheme, these events occur in a definite order. But what the causal graph shows is that the result we get doesn’t require that order—and indeed allows these events to occur “in parallel”.
Many lambdas don’t allow parallelization in their evaluation, so have simple, linear causal graphs:
It’s common to have simple branching in the causal graph—associated with pieces of the λ expression that are completely separated as far as beta reduction is concerned, and can be evaluated separately:
One tricky issue that arises in constructing causal graphs for lambdas is figuring out exactly what is really dependent on what. In this case it might seem that the two events are independent, since the first one involves λ[a,…] while the second one involves λ[b,...]. But the second one can’t happen until the λ[b, ...] is “activated” by the reduction of λ[a, ...] in the first event—with the result that second event must be considered causally dependent on the first, as recorded in the causal graph:
While many lambdas have simple, linear or branched causal graphs, plenty have more complicated structures. Here are some examples for lambdas that terminate:
Lambdas that don’t terminate have infinite causal graphs:
But what’s notable here is that even when the evolution—as visualized in terms of the sequence of sizes of lambdas—isn’t simple, the causal graph is still usually quite simple and repetitive. And, yes, in some cases seeing this may well be tantamount to a proof that the evolution of the lambda won’t terminate. But a cautionary point is that even for lambdas that do terminate, we saw above that their causal graphs can still look essentially repetitive—right up to when they terminate.
The causal graphs we showed in the previous section are all based on analyzing causal dependencies in specific lambda evaluation chains, generated with our standard (leftmost outermost) evaluation scheme. But—just like in our Physics Project—it’s also possible to generate multiway causal graphs, in which we show causal connections between all states in the multiway graph representing all possible evaluation sequences.
Here’s the multiway version of the first causal graph we showed above:
Some causal graphs remain linear even in the multiway case, but others split into many paths:
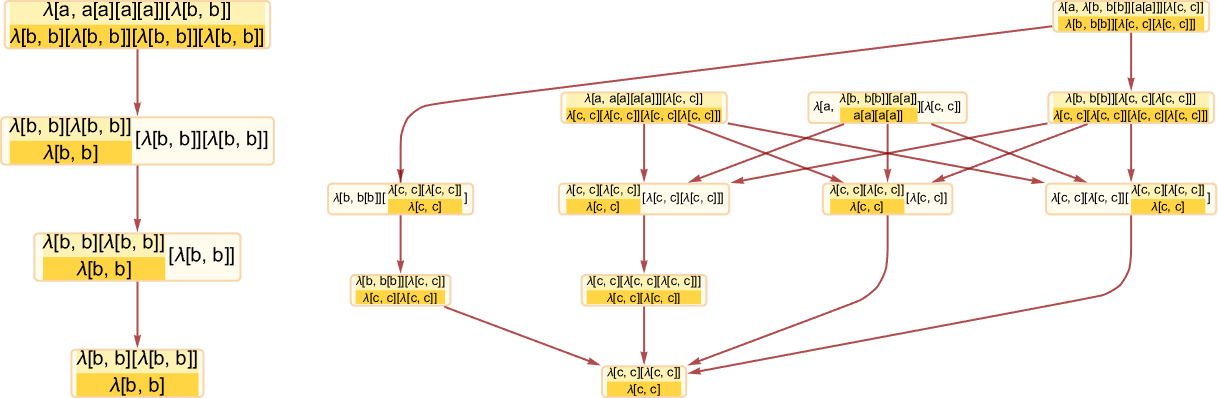
It’s fairly typical for multiway causal graphs to be considerably more complicated than ordinary causal graphs. So, for example, while the ordinary causal graph for [1(11)][[212]] is
the multiway version is

while the multiway graph for states is:
So, yes, it’s possible to make multiway causal graphs for lambdas. But what do they mean? It’s a somewhat complicated story. But I won’t go into it here—because it’s basically the same as the story for combinators, which I discussed several years ago. Though lambdas don’t allow one to set up the kind of shared-subexpression DAGs we considered for combinators; the variables (or de Bruijn indices) in lambdas effectively lead to long-range correlations that prevent the kind of modular treelike approach we used for combinators.
We’ve seen that in general lambdas can do very complicated things. But there’s a particular class of lambdas—the “linear lambdas”—that behave in much simpler ways, allowing them to be rather completely analyzed. A linear lambda is a lambda in which every variable appears only once in the body of the lambda. So this means that λ[a, a] is a linear lambda, but λ[a, a[a]] is not.
The first few linear lambdas are therefore
or in de Bruijn index form:
Linear lambdas have the important property that under beta reduction they can never increase in size. (Without multiple appearances of one variable, beta reduction just removes subexpressions, and can never lead to the replication of a subexpression.) Indeed, at every step in the evaluation of a linear lambda, all that can ever happen is that at most one λ is removed:

Since linear lambdas always have one variable for each λ, their size is always an even number.
The number of linear lambdas is small compared to the total number of lambdas of a given size:

(Asymptotically, the number of linear lambdas of size 2m grows like 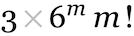 .)
.)
Here are the Tromp diagrams for the size-6 linear lambdas:
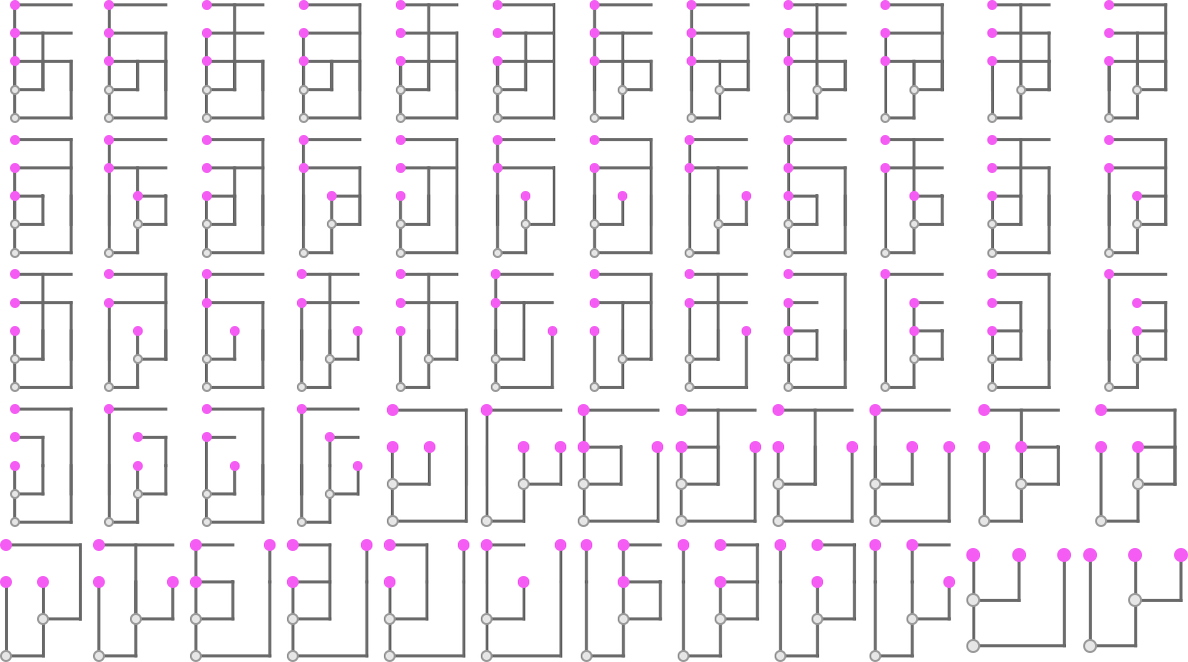
Evaluation always terminates for a linear lambda; the number of steps it takes is independent of the evaluation scheme, and has a maximum equal to the number of λ’s; the distribution for size-6 linear lambdas is:
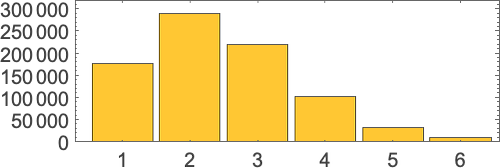
The multiway graphs for linear lambdas are rather simple. Since every λ is independent of every other, it never matters in what order they are reduced, and the multiway graph consists of a collection of diamonds, as in for example:
For size 6 the possible multiway graphs (with their multiplicities) are:

For size 8 it’s
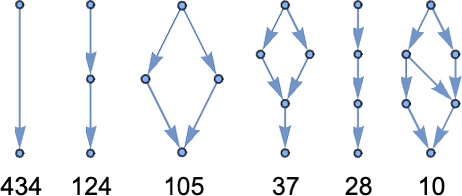
where the last graph can be drawn in a more obviously symmetrical way as:
And for size 10 it’s:
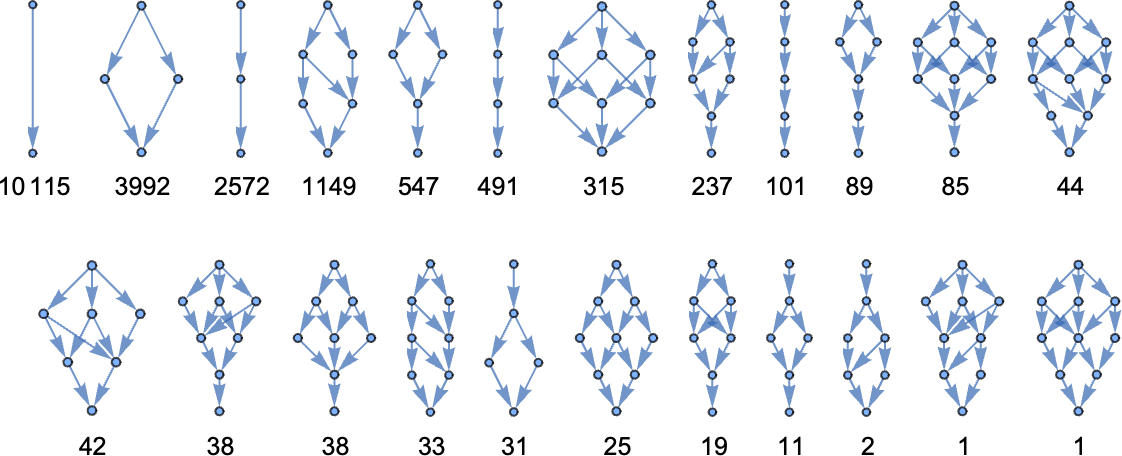
In addition to looking at linear lambdas, we can also look at affine lambdas, which are defined to allow zero as well as one instance of each variable. The affine lambdas behave in a very similar way to the linear lambdas, except that now there are some “degenerate diamond structures” in the multiway graph, as in:
So now that we’ve explored all this ruliology for lambdas, how does it compare to what I found several years ago for combinators? Many of the core phenomena are certainly very much the same. And indeed it’s easy to convert between lambdas and combinators—though a lambda of one size may correspond to a combinator of a rather different size.
For example, the size-4 lambdas have these equivalent combinators (where several of the combinators are the same, because the lambdas—at least when fed an appropriate number of arguments—end up evaluating to the same canonical form):

Meanwhile, the size-3 combinators have these equivalent lambdas:

Not surprisingly, the (LeafCount) size of lambdas tends to be slightly smaller for the equivalent combinators, because the presence of de Bruijn indices means lambdas effectively have a larger “alphabet” to work with.
But in the end, lambdas and combinators can “do all the same things”, as in these cases:

The Principle of Computational Equivalence implies that at a fundamental level the ruliology of systems whose behavior is not obviously simple will be at least at some level the same.
But lambdas have definitely given us some unique challenges. First, there is the matter of variables and the nonlocality they imply. It’s not like in a cellular automaton or a Turing machine where in a sense every update happens locally. Nor is it even like in combinators, where things are local at least on a tree—or hypergraph rewriting systems where things are local on a hypergraph. Lambdas are both hierarchical and nonlocal. Lambda expressions have a tree structure, but variables knit pieces of this tree together in arbitrarily complex ways. And beta reduction can in effect pull on arbitrarily long threads.
All of this then gets entangled with another issue: lambdas routinely can get very big. And even that wouldn’t be such a problem if it wasn’t for the fact that there’s no obvious way to compress what the lambdas do. With the result that even though the Wolfram Language gives one a very efficient way to deal with symbolic structures, the things I’ve done here have often challenged my computational resources.
Still, in the end, we’ve managed to do at least the basics in exploring the ruliology of lambdas, and have seen that yet another corner of the computational universe is full of remarkable and surprising phenomena. I first wondered what lambdas might be “like in the wild” back at the beginning of the 1980s. And I’m pleased that finally now—so many years later—I’ve finally been able to get a sense of the world of lambdas and both the uniqueness and the sameness of their ruliology.
An immense amount has been written about lambdas over the past 90 years, though in most cases its focus has been formal and theoretical, not empirical and ruliological. When I wrote about combinators in 2020 I did the scholarship to compile a very extensive bibliography of the (considerably smaller) literature about combinators. For lambdas I have not attempted a similar exercise. But given the overlap—and equivalence—between combinators and lambdas, much of my combinator bibliography also applies to lambdas.
Thanks to Wolfram Institute Fellows Nik Murzin and Willem Nielsen for extensive help. Also thanks to several others affiliated with the Wolfram Institute, especially Richard Assar and Joseph Stocke. In addition, for specific input about what I describe here I thank Alex Archerman, Utkarsh Bajaj, Max Niederman, Matthew Szudzik, and Victor Taelin. Over the years I’ve interacted about lambdas with many people, including Henk Barendregt, Greg Chaitin, Austin Jiang, Jan Willem Klop, Roman Maeder, Dana Scott and John Tromp. And at a practical level I’ve had innumerable discussions since the late 1970s about the Function function in Wolfram Language and Mathematica, as well as its predecessor in SMP.
Note added September 18, 2025: I thank John Tromp for suggesting several significant improvements to the original version of this.
2025-08-15 06:05:53

Several often arrive in a single day. Sometimes they’re marked “urgent”. Sometimes they’re long. Sometimes they’re short. Sometimes they’re humble. Sometimes they’re conspiratorial. And sometimes, these days, they’re written “in collaboration with” an AI. But there’s a common theme: they’re all emails that present some kind of fundamental theory invented by their authors (or perhaps their AI) about how our universe works.
At some level it’s encouraging to see how many people find it interesting to think about fundamental questions in science. But at some level it’s also to me very frustrating. All that effort being spent. And so much of it so wide of the mark. Most of the time it’s based on at best high-school physics—missing everything that was learned in twentieth-century physics. Sometimes it’s easy to tell that what’s being said just can’t be right; often things are too vague or tangled for one to be able to say much.
Most physicists term people who send such theories “crackpots”, and either discard their missives or send back derisive responses. I’ve never felt like that was the right thing to do. Somehow I’ve always felt as if there has to be a way to channel that interest and effort into something that would be constructive and fulfilling for all concerned. And maybe, just maybe, I now have at least one idea in that direction.
It doesn’t help the situation of course that there are so many myths floating around about how science makes progress. Newton suddenly figured out gravity when an apple fell on his head. Einstein was a lowly clerk when he figured out relativity. When one actually studies the history of science one finds that—essentially without exception—there’s always a long and sophisticated personal backstory to advances people make. Newton was already a top professor when the (perhaps apocryphal) apple fell. Einstein had got a PhD from a top university, and had then gone to the Silicon Valley of the time, the Swiss patent office.
It basically never happens that there are sudden flashes of insight that come out of nowhere. And that’s particularly true in fundamental physics, where a fairly tall tower of abstraction and formalism has developed, particularly over the past century or so. There’s everyday physics, of the kind we can reason about from our everyday experience. And then there’s physics of the very large and very small that’s far from our everyday experience. But it’s that physics that’s our best probe of the fundamentals of how things work. And if you don’t know it, you’re at a crippling disadvantage in making foundational progress in physics.
Of course, I would be the first to say that in science “conventional wisdom” often leads one astray. There need to be new, fresh ideas. And often ones that challenge the foundations of things that have long been assumed. But when—as in physics—there’s methodological depth to what’s been figured out, that’s a good place to start in making further progress. Maybe the traditional mathematical approach to quantum field theory isn’t quite right. But to discard all the abstractions and generalizations that got us to quantum field theory, and to return, for example, to high-school physics takes us to the wrong level of thinking.
What’s the story of my own efforts at figuring out fundamental physics? The past few years have been exciting times for me. Building on basically a lifetime of science and technology to arrive—to my great surprise—at what seems to be a serious breakthrough in understanding fundamental physics and how our universe works. And while what’s now our Wolfram Physics Project can at a superficial level be explained fairly simply, what’s underneath is quite a tower of ideas, formalism and computational investigations.
At some level, though, I’m an “amateur physicist”, doing science as a hobby—like the people who write to me. But under the surface, the story is rather different. Yes, for nearly four decades my main day job has been CEOing a tech company. But (as a mid teenager) I started out doing physics, and soon was a rather successful professional physicist. And indeed a key motivation for my efforts in technology has always been to build tools I want for myself for doing science. So, yes, over the years I’ve indeed maintained what one might call a “serious hobby” of doing science (now, for example, with the Wolfram Institute).
It has to be said that I’m pretty sure I wouldn’t have been able to do the things I’ve done if I’d stayed embedded in the academic system—with its increasingly strong toe-the-line constraints. It’s been crucial that I’ve been in a situation where I’m free to chart my own independent intellectual path. But despite that institutional independence I’m still routinely leveraging my rather extensive knowledge of existing physics. It’s true that the new paradigm I’ve built has led me to reject some of what has long been believed. But I’ve never rejected anything lightly. I always make a point of thoroughly understanding what I’m rejecting—and as part of that it’s become my practice to make a detailed study of its history, to see just how people originally came to believe it.
If you just catch something I say on a podcast you might get the idea that the things I’ve figured out just came to me in the simple way I describe them. But it’s not like that at all. It’s always a complicated process, full of detailed, systematic work. Central to the way I do things is the tower of technology we’ve built over the past four decades. I use Wolfram Language as a medium to clarify my thoughts. And I use it to make those thoughts concrete in computer experiments—which routinely produce results I absolutely did not expect. As much as possible, I insist on trying to understand everything from its first principles, so I can be confident that I know what I’m talking about. (Oh, and it also helps that I work with very talented people, and have a large network that includes many of the world’s leading scientists.)
So, yes, even if I manage to explain it simply, there’s always all sorts of sophistication behind the science I do. So when I get an email that says “I just figured out physics yesterday”, or “there’s this high-school physics fact that explains the universe” it profoundly doesn’t ring true. Even if someone says “an AI helped me” and there’s a veneer of technical academic presentation.
In 1975—when I was 15 years old—I had just started writing papers about my own physics research when I received a curious letter, now preserved as a yellowing page in my archives:


Its author went on to describe (at length) his “Hoop Hypothesis”—that particles like electrons and protons are in effect little loops of wire carrying electric current:
There seemed to be things that were obviously wrong, so I decided I’d point them out (Eton College was the high school I was at; the “New Buildings” were from the 1840s):



Yes, I was a lot younger then (with a duly immature signature!). And I didn’t anticipate that after my first response I’d receive a deluge of letters full of elaborate handwritten calculations. I responded a couple of times, but didn’t seem to be making any headway. And so I gave up. But then I started getting letters saying “please send back my calculations”. My archives still contain the envelope I’d prepared to do that. But I felt I should say something definitive to close things off. And I never got around to that. Which I feel a little bad about…
But looking at the letter I received half a century ago it’s striking how similar it is to so many of the emails I get today (though today the writing is not usually so eloquent). Somehow there’s an enthusiasm for “solving physics” using everyday thinking and everyday experience that’s persisted all that time, and about which people who haven’t been deeply exposed to twentieth-century physics develop surprisingly great conviction.
Let’s say you’re passionately interested in doing science, but you haven’t had a chance to spend years learning the technical details of something like existing physics. What can you do?
Maybe you have some particular idea, perhaps based on something you’ve heard about or read about. If the idea is an area with as much technical depth as physics, it’s realistically going to be an immense challenge to develop the idea in a useful way. And most likely to really do so you’d have to learn a whole tower of technical details—the equivalent of several years of schooling.
But nowadays, you might think: “Can’t AI help?” Well, if you tell your idea to a high-end LLM it’ll probably be able to produce something about it that looks and feels like a scientific paper. But unfortunately with almost absolute certainty the paper will ultimately be complete nonsense. At a sentence-by-sentence or even paragraph-by-paragraph level it may seem OK. But—assuming your idea hasn’t already been worked out somewhere on the internet for the AI to read—then regardless of how much “reasoning” the AI claims it’s doing, it’s almost astronomically unlikely that it’ll produce anything that hangs together.
But while AI on its own isn’t realistically going to help, computers and computation potentially can. Because if you can get your idea “beyond pure words” to something more formal and precise, then it’s potentially a different story. Because then you may be able to do the kind of thing I’ve routinely done for so long, and use the power of computation to do the “heavy lifting” to explore your ideas. And, yes, it’s an ideal use case for the Wolfram Language. Because the Wolfram Language not only lets you describe things to a computer; it also helps you formulate your ideas in clear, computational form. And these days there’s even a good chance you’ll be able to use our AI Notebook Assistant to help you get started.
But the thing to emphasize is that if this is going to work, you’ll at some point have to actually understand—with clarity—the computational language code to describe your idea. It’s a high bar to reach if you start “just with words”. But if you reach it (or get someone to help you reach it) you’ll be off and running, able to do “real science”, relying on a computer and Wolfram Language just like so many of the world’s leading scientists do.
If I’m realistic, though, only a tiny fraction of the “avocational science” emails I receive seem even close to being amenable to this kind of formalization. And most of the time I just feel they picked the wrong battle. They’re trying to “solve physics” and “beat Einstein”. But, as I’ve explained, you have to have a lot of technical knowledge to even credibly get to the starting gate in such an effort.
So is that the end of the story? Are the front lines of science just closed to anyone who isn’t in the “priesthood” of highly trained scientists? Well, you’ve got to expect to do careful, systematic work. But the good news is that these days there’s a certain opportunity for great, foundational contributions to be made that don’t depend on all the technical details of, say, existing physics.
Yes, in these years, there’s a way for someone without all that technical training to do foundational science that’s significant and thoroughly original—and potentially has all sorts of philosophical as well as scientific significance. It won’t be something that “swoops in and solves physics”. But it can be a building block that might even apply to physics—and that represents a lasting intellectual contribution.
As it happens, it’s been my own work over the past 45 or so years that’s perhaps most clearly highlighted what’s possible. But ultimately what’s opened up the opportunity is that great intellectual development of our time: the computational paradigm. Unaided, there would be no alternative but to toil through all those technical details to reach frontiers of science. But what we’re learning is that thinking in fundamentally computational terms provides something transformative: a way to see directly deep into the foundations of science. And for those who choose to use it, a way to chart a direct path right to the frontiers.
In the past it wouldn’t have been so clear. But particularly now with our Physics Project and everything that’s followed from it, I think we can be confident that there are meaningful computational foundations to be found for theoretical science, “underneath”, for example, fields like physics and mathematics. And it’s these foundations that—with the help of computation—give us access to a new frontier of science.
It’s all about exploring the computational universe—the universe of computational possibilities. The computational universe is infinite. And there’s a place in it for everyone. A place that’s never been visited before. Where there’s new science to be found—that, once found, will stand forever.
These days I have a name for this type of science. I call it ruliology: the study of systems with (usually simple) computational rules. In some ways one can view ruliology as the ultimate theoretical science: the science from which other sciences must flow. I myself have been doing ruliology for 45 years now, and it’s been at the heart of most of the discoveries I’ve made over all those years. But in all that I’ve done I haven’t even begun to scratch the surface of what there is to discover in ruliology.
Pick even perhaps the single best-explored part of ruliology: the study of cellular automata. Going out into the computational universe one can instantly find examples full of all sorts of richness that one can be pretty sure nobody has ever seen before:

Each of these is like a world unto itself: a system with all sorts of detailed behavior that can be studied. It needs scientific creativity to figure out what to look at. And it needs a certain clarity of thinking to keep track of what one might find. But with Wolfram Language as a tool, there’s no limit to the explorations one can do.
Create a computational essay describing them, and you’ll have made a clear contribution to science. Don’t expect that the details of what you’ll see will immediately relate to phenomena, say, in physics. Even if you’re using hypergraphs, multiway systems, etc. you’re inevitably operating far below even what physics over the past century has explored. But the more broadly and deeply you investigate, the more you’ll have a chance to find core phenomena in ruliology that’ll flow through to lots of other places, including potentially physics.
By doing computer experiments you’ll develop a new kind of intuition. I don’t think I’ve ever seen someone who isn’t at first surprised by what they see out in the computational universe once they carefully look at it. But with that intuition you’ll get a sense of what you might explore in the computational universe. And you’ll get a real, “21st-century” way to think about science. Something that in the end might lead you not only to specific scientific conclusions but also much deeper and more general conceptual or philosophical conclusions.
Everyday experience of the world gives one a certain intuition, whose implications have been well worked through over the millennia. But experience of the computational universe is something new, and something from which—if one successfully internalizes it—one can derive fundamentally new thoughts about the way things work.
So what does this mean for the stream of emails I receive? Just sometimes there’s already a piece of ruliology. Where there’s a clear, computational phenomenon that the mail describes. And when I get such mail I think to myself “yes, there’s something that’ll be a surviving contribution to science”. But far too often the thrust of the mail is instead “here’s a theory I came up with by making an argument, largely with words”. Centuries ago that might have been par for the course. But now nothing like that has a serious chance of reaching the frontiers of something like physics.
And it could be that the only way to reach those frontiers would be to learn the whole tower of existing physics. But ruliology provides a unique shortcut. Ruliology is a field so vast, and so comparatively new, that in a sense we’re inevitably all at some level beginners in it. I’ve spent years building tools for it, that through Wolfram Language are now available to everyone. So now we’re all able to explore it together.
When one makes a discovery in ruliology, there’s a certain abstract permanence to it. That rule you found will always do that thing. It’s something that in a sense helps to elevate us beyond our mere human existence. We’ve come upon something that’s forever, that will always be that way. And it’s hard not to feel a sense of awe in being able to discover a thing like that, and to know that no human in history has ever seen it before.
I’d like to think that this kind of thing is the essence of what people seek when they try to come up with their “theories of physics”. But the difference is that a solid piece of ruliology—likely complete with striking and unexpected images—represents a real achievement in science that one can validly be proud of, and that can enter the long-term canon of science.
So, please, send ruliology, not yet more vague theories of physics! Let’s take all that energy and direct it to that foundational mission of 21st-century science: the systematic exploration of the computational universe.
The best way to start studying ruliology is to start doing it. Check out some of the things I have written about ruliology. Click any picture in any piece and you’ll get Wolfram Language to reproduce that picture. Start by finding a picture you think looks interesting. Try modifying its code, and try to understand what’s going on. We’re planning to put in place a systematic educational program for ruliology, as well as setting up a new, modern venue for publishing ruliological investigations. And we’re planning to provide infrastructure to help develop a systematic worldwide ruliological community.
Add yourself here to learn about developments with doing ruliology ›
2025-08-06 01:52:24
![]()
Version 14.2 launched on January 23 of this year. Now, today, just over six months later, we’re launching Version 14.3. And despite its modest .x designation, it’s a big release, with lots of important new and updated functionality, particularly in core areas of the system.
I’m particularly pleased to be able to report that in this release we’re delivering an unusually large number of long-requested features. Why didn’t they come sooner? Well, they were hard—at least to build to our standards. But now they’re here, ready for everyone to use.
Those who’ve been following our livestreamed software design reviews (42 hours of them since Version 14.2) may get some sense of the effort we put into getting the design of things right. And in fact we’ve been consistently putting in that kind of effort now for nearly four decades—ever since we started developing Version 1.0. And the result is something that I think is completely unique in the software world—a system that is consistent and coherent through and through, and that has maintained compatibility for 37 years.
It’s a very big system now, and even I sometimes forget some of the amazing things it can do. But what now routinely helps me with that is our Notebook Assistant, released late last year. If I’m trying to figure out how to do something, I’ll just type some vague description of what I want into the Notebook Assistant. The Notebook Assistant is then remarkably good at “crispening up” what I’m asking, and producing relevant pieces of Wolfram Language code.
Often I was too vague for that code to be exactly what I want. But it almost always puts me on the right track, and with small modifications ends up being exactly what I need.
It’s a very good workflow, made possible by combining the latest AI with the unique characteristics of the Wolfram Language. I ask something vague. The Notebook Assistant gives me precise code. But the crucial thing is that the code isn’t programming language code, it’s Wolfram Language computational language code. It’s code that’s specifically intended to be read by humans and to represent the world computationally at as high a level as possible. The AI is going to behave in the kind of heuristic way that AIs do. But when you pick out the Wolfram Language code you want, you get something precise that you can build on, and rely on.
It’s amazing how important the design consistency of the Wolfram Language is in so many ways. It’s what allows the different facets of the language to interoperate so smoothly. It’s what makes it easy to learn new areas of the language. And, these days, it’s also what makes it easy for AIs to use the language well—calling on it as a tool much like humans do.
The fact that the Wolfram Language is so consistent in its design—and has so much built into it—has another consequence too: it means that it’s easy to add to it. And over the last 6 years, a rather staggering 3200+ add-on functions have been published in the Wolfram Function Repository. And, yes, quite a few of these functions may end up developing into full, built-in functions, though sometimes a decade or more hence. But here and now the Notebook Assistant knows about them in their current form—and can automatically show you where they might fit into things you’re doing.
OK, but let’s get back to Version 14.3. Where there’s a lot to talk about…
I started using computers with screens in 1976. And back then every screen was black, and the text on it was white. In 1982, when “workstation” computers came out, it switched around, and I started using displays that looked more like printed pages, with black text on white backgrounds. And that was the usual way things worked—for several decades. Then, a little more than five years ago, “dark mode” started to be popular—and one was back to 1970s-style displays, of course now with full color, at much higher resolution, etc. We’ve had “dark mode styles” available in notebooks for a long time. But now, in Version 14.3, we have full support for dark mode. And if you set your system to Dark Mode, in Version 14.3 all notebooks will by default automatically display in dark mode:
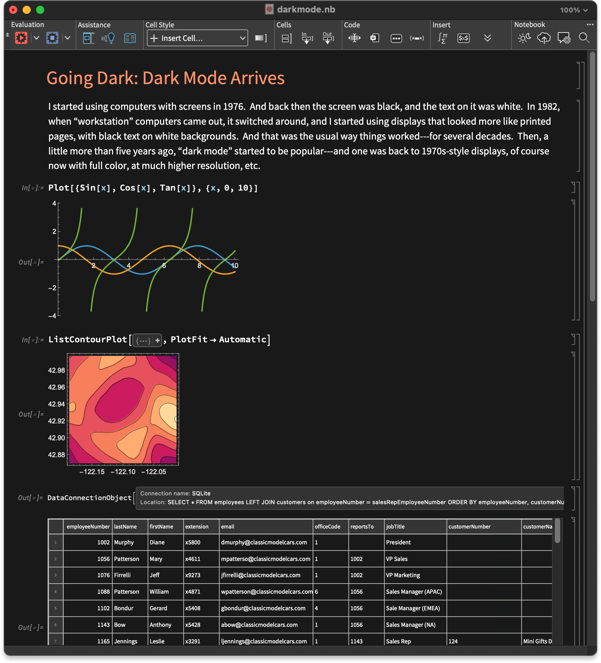
You might think: isn’t it kinda trivial to set up dark mode? Don’t you just have to change the background to black, and text to white? Well, actually, there’s a lot, lot more to it. And in the end it’s a rather complex user interface—and algorithmic—challenge, that I think we’ve now solved very nicely in Version 14.3.
Here’s a basic question: what should happen to a plot when you go to dark mode? You want the axes to flip to white, but you want the curves to keep their colors (otherwise, what would happen to text that refers to curves by color?). And that’s exactly what happens in Version 14.3:
Needless to say, one tricky point is that the colors of the curves have to be chosen so they’ll look good in both light and dark mode. And actually in Version 14.2, when we “spiffed up” our default colors for plots, we did that in part precisely in anticipation of dark mode.
In Version 14.3 (as we’ll discuss below) we’ve continued spiffing up graphics colors, covering lots of tricky cases, and always setting things up to cover dark mode as well as light:


But graphics generated by computation aren’t the only kind of thing affected by dark mode. There are also, for example, endless user interface elements that all have to be adapted to look good in dark mode. In all, there are thousands of colors affected, all needing to be dealt with in a consistent and aesthetic way. And to do this, we’ve ended up inventing a whole range of methods and algorithms (which we’ll eventually make externally available as a paclet).
And the result, for example, is that something like the notebook can essentially automatically be configured to work in dark mode:

But what’s happening underneath? Needless to say, there’s a symbolic representation that’s involved. Normally, you specify a color as, for example, RGBColor[1,0,0]. But in Version 14.3, you can instead use a symbolic representation like:
In light mode, this will display as red; in dark mode, pink:
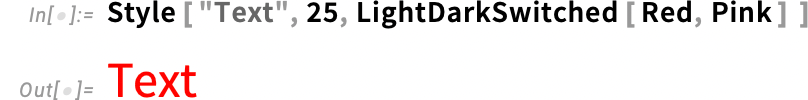

If you just give a single color in LightDarkSwitched, our automatic algorithms will be used, in this case producing in dark mode a pinkish color:
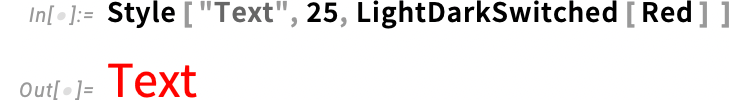

This specifies the dark mode color, automatically deducing an appropriate corresponding light mode color:

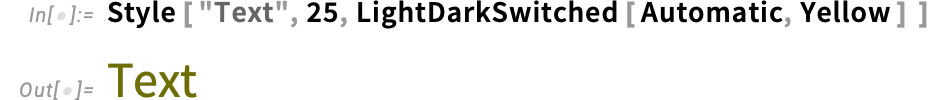
But what if you don’t want to explicitly insert LightDarkSwitched around every color you’re using? (For example, say you already have a large codebase full of colors.) Well, then you can use the new style option LightDarkAutoColorRules to specify more globally how you want to switch colors. So, for example, this says to do automatic light-dark switching for the “listed colors” (here just Blue) but not for others (e.g. Red):
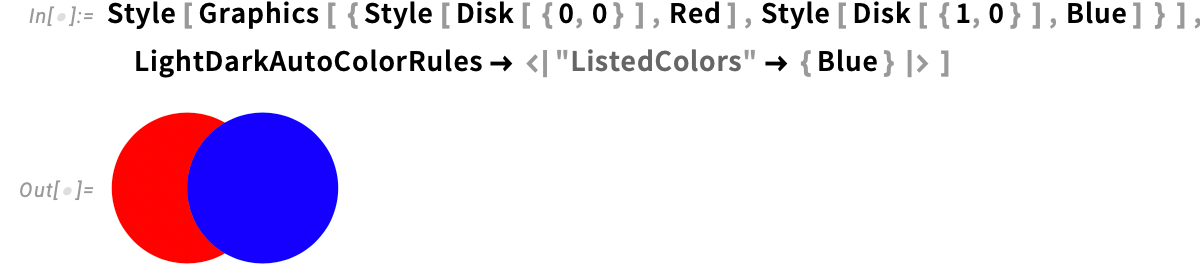

You can also use LightDarkAutoColorRules ![]() All which uses our automatic switching algorithms for all colors:
All which uses our automatic switching algorithms for all colors:


And then there’s the convenient LightDarkAutoColorRules ![]() "NonPlotColors" which says to do automatic switching, but only for colors that aren’t our default plot colors, which, as we discussed above, are set up to work unchanged in both light and dark mode.
"NonPlotColors" which says to do automatic switching, but only for colors that aren’t our default plot colors, which, as we discussed above, are set up to work unchanged in both light and dark mode.
There are many, many subtleties to all this. As one example, in Version 14.3 we’ve updated many functions to produce light-dark switched colors. But if those colors were stored in a notebook using LightDarkSwitched, then if you took that notebook and tried to view it with an earlier version those colors wouldn’t show up (and you’d get error indications). (As it happens, we already quietly introduced LightDarkSwitched in Version 14.2, but in earlier versions you’d be out of luck.) So how did we deal with this backward compatibility for light-dark switched colors our functions produce? Well, we don’t in fact store these colors in notebook expressions using LightDarkSwitched. Instead, we just store the colors in ordinary RGBColor etc. form, but the actual r, g, b values are numbers that have their “switched versions” steganographically encoded in high-order digits. Earlier versions just read this as a single color, imperceptibly adjusted from what it usually is; Version 14.3 reads it as a light-dark switched color.
We’ve gone to a lot of effort to handle dark mode within our notebooks. But operating systems also have ways of handling dark mode. And sometimes you just want to have colors that follow the ones in your operating system. In Version 14.3 we’ve added SystemColor to do this. So, for example, here we say we want the background inside a frame to follow—in both light and dark mode—the color your operating system is using for tooltips:


One thing we haven’t explicitly mentioned yet is how textual content in notebooks is handled in dark mode. Black text is (obviously) rendered in white in dark mode. But what about section headings, or, for that matter, entities?
![]()

Well, they use different colors in light and dark mode. So how can you use those colors in your own programs? The answer is that you can use ThemeColor. ThemeColor is actually something we introduced in Version 14.2, but it’s part of a whole framework that we’re progressively building out in successive versions. And the idea is that ThemeColor allows you to access “theme colors” associated with particular “themes”. So, for example, there are "Accent1", etc. theme colors that—in a particular blend—are what’s used to get the color for the "Section" style. And with ThemeColor you can access these colors. So, for example, here is text in the "Accent3" theme color:

And, yes, it switches in dark mode:

Alright, so we’ve discussed all sorts of details of how light and dark mode work. But how do you determine whether a particular notebook should be in light or dark mode? Well, usually you don’t have to, because it’ll get switched automatically, following whatever your overall system settings are.
But if you want to explicitly lock in light or dark mode for a given notebook, you can do this with the ![]() button in the notebook toolbar. And you can also do this programmatically (or in the Wolfram System preferences) using the LightDark option.
button in the notebook toolbar. And you can also do this programmatically (or in the Wolfram System preferences) using the LightDark option.
So, OK, now we support dark mode. So… will I turn the clock back for myself by 45 years and return to using dark mode for most of my work (which, needless to say, is done in Wolfram Language)? Dark mode in Wolfram Notebooks looks so nice, I think I just might…
In some ways the whole story of the Wolfram Language is about “AI”. It’s about automating as much as possible, so you (as a human) just have to “say what you want”, and then the system has a whole tower of automation that executes it for you. Of course, the big idea of the Wolfram Language is to provide the best way to “say what you want”—the best way to formalize your thoughts in computational terms, both so you can understand them better, and so your computer can go as far as it needs to work them out. Modern “post-ChatGPT” AI has been particularly important in adding a thicker “linguistic user interface” for all this. In Wolfram|Alpha we pioneered natural language understanding as a front end to computation; modern LLMs extend that to let you have whole conversations in natural language.
As I’ve discussed at some length elsewhere, what the LLMs are good at is rather different from what the Wolfram Language is good at. At some level LLMs can do the kinds of things unaided brains can also do (albeit sometimes on a larger scale, faster, etc.). But when it comes to raw computation (and precise knowledge) that’s not what LLMs (or brains) do well. But of course we know a very good solution to that: just have the LLM use Wolfram Language (and Wolfram|Alpha) as a tool. And indeed within a few months of the release of ChatGPT, we had set up ways to let LLMs call our technology as a tool. We’ve been developing ever better ways to have that happen—and indeed we’ll have a major release in this area soon.
It’s popular these days to talk about “AI agents” that “just go off and do useful things”. At some level the Wolfram Language (and Wolfram|Alpha) can be thought of as “universal agents”, able to do the full range of “computational things” (as well as having connectors to an immense number of external systems in the world). (Yes, Wolfram Language can send email, browse webpages—and “actuate” lots of other things in the world—and it’s been able to do these things for decades.) And if one builds the core of an agent out of LLMs, the Wolfram Language (and Wolfram|Alpha) serve as “universal tools” that the LLMs can call on.
So although LLMs and the Wolfram Language do very different kinds of things, we’ve been building progressively more elaborate ways for them to interact, and for one to be able to get the best from each of them. Back in mid-2023 we introduced LLMFunction, etc. as a way to call LLMs from within the Wolfram Language. Then we introduced LLMTool as a way to define Wolfram Language tools that LLMs can call. And in Version 14.3 we have another level in this integration: LLMGraph.
The goal of LLMGraph is to let you define an “agentic workflow” directly in Wolfram Language, specifying a kind of “plan graph” whose nodes can give either LLM prompts or Wolfram Language code to run. In effect, LLMGraph is a generalization of our existing LLM functions—with additional features such as the ability to run different parts in parallel, etc.
Here’s a very simple example: an LLMGraph that has just two nodes, which can be executed in parallel, one generating a haiku and one a limerick:

We can apply this to a particular input; the result is an association (which here we format with Dataset):

Here’s a slightly more complicated example—a workflow for summarizing text that breaks the text into chunks (using a Wolfram Language function), then runs LLM functions in parallel to do the summarizing, then runs another LLM function to make a single summary from all the chunk summaries:

This visualizes our LLMGraph:
If we apply our LLMGraph, here to the US Constitution, we get a summary:

There are lots of detailed options for LLMGraph objects. Here, for example, for our "ChunkSummary" we used a "ListableLLMFunction" key, which specifies that the LLMFunction prompt we give can be threaded over a list of inputs (here the list of chunks generated by the Wolfram Language code in "TextChunk").
An important feature of LLMGraph is its support for “test functions”: nodes in the graph that do tests which determine whether another node needs to be run or not. Here’s a slightly more complicated example (and, yes, the LLM prompts are necessarily a bit verbose):

This visualizes the LLM graph:
Run it on a correct computation and it just returns the computation:
But run it on an incorrect computation and it’ll try to correct it, here correctly:

This is a fairly simple example. But—like everything in Wolfram Language—LLMGraph is built to scale up as far as you need. In effect, it provides a new way of programming—complete with asynchronous processing—for the “agentic” LLM world. Part of the ongoing integration of Wolfram Language and AI capabilities.
Let’s say you plot some data (and, yes, we’re using the new tabular data capabilities from Version 14.2):
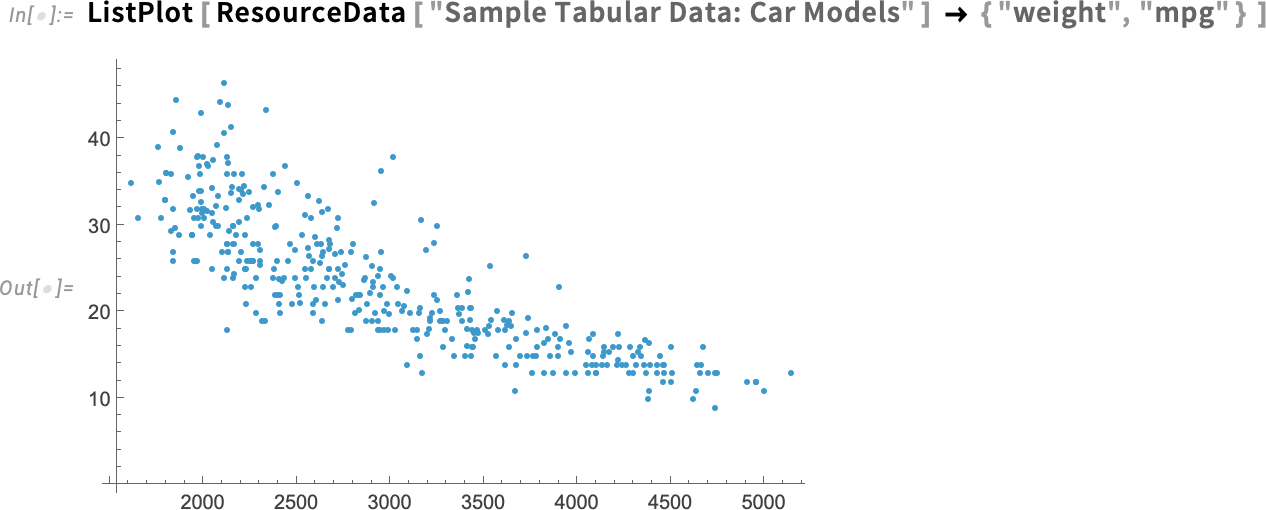
What’s really going on in this data? What are the trends? Often one finds oneself making some kind of fit to the data to try to find that out. Well, in Version 14.3 there’s now a very easy way to do that: ListFitPlot:
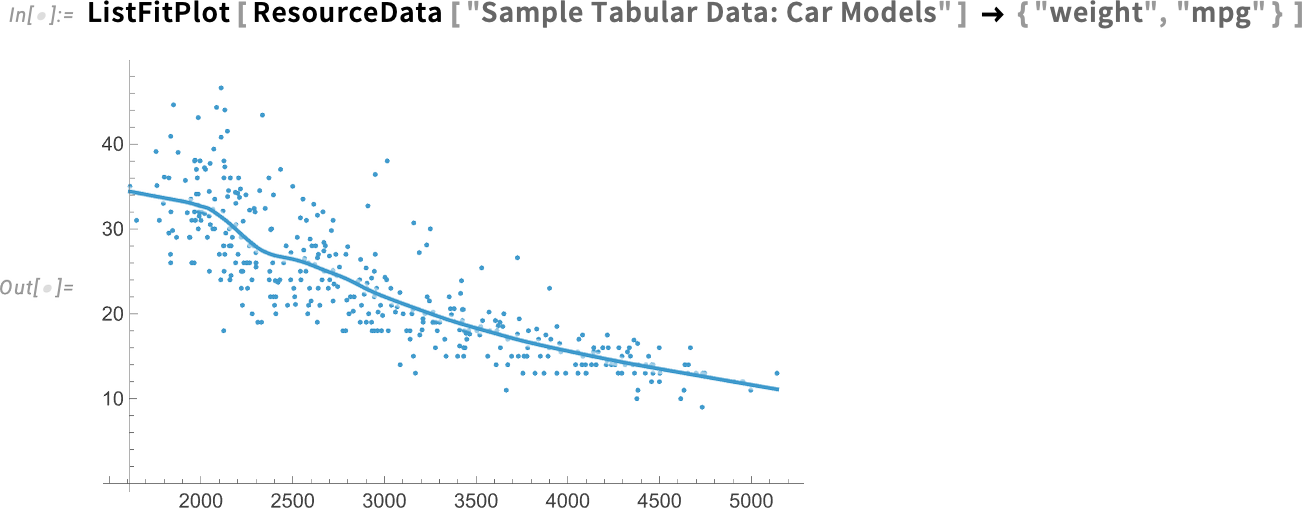
This is a local fit to the data (as we’ll discuss below). But what if we specifically want a global linear fit? There’s a simple option for that:
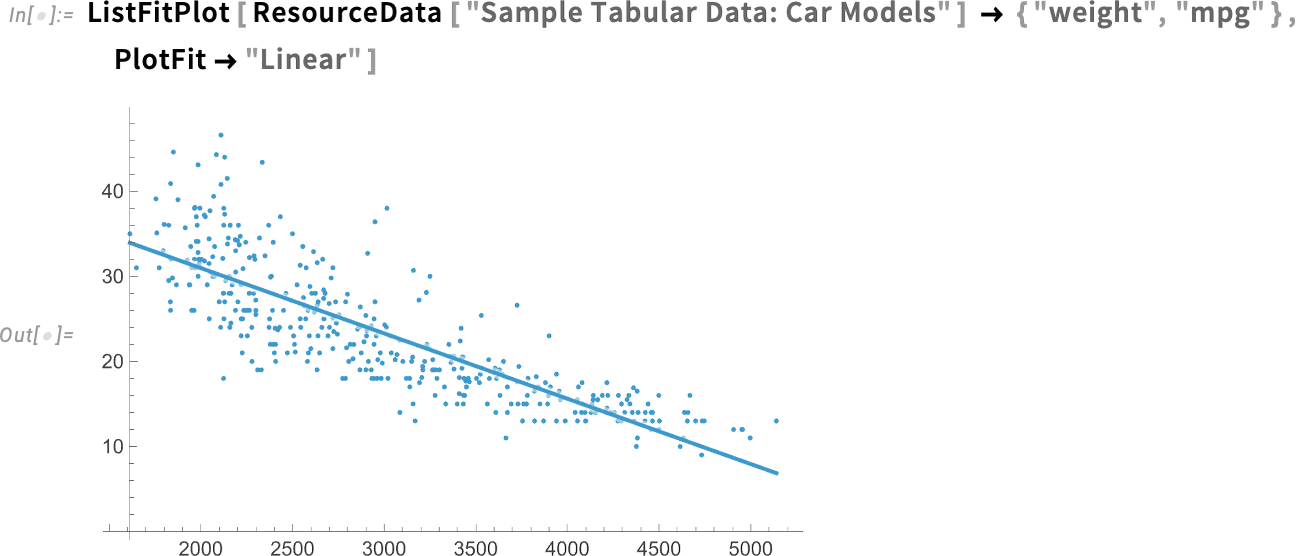
And here’s an exponential fit:
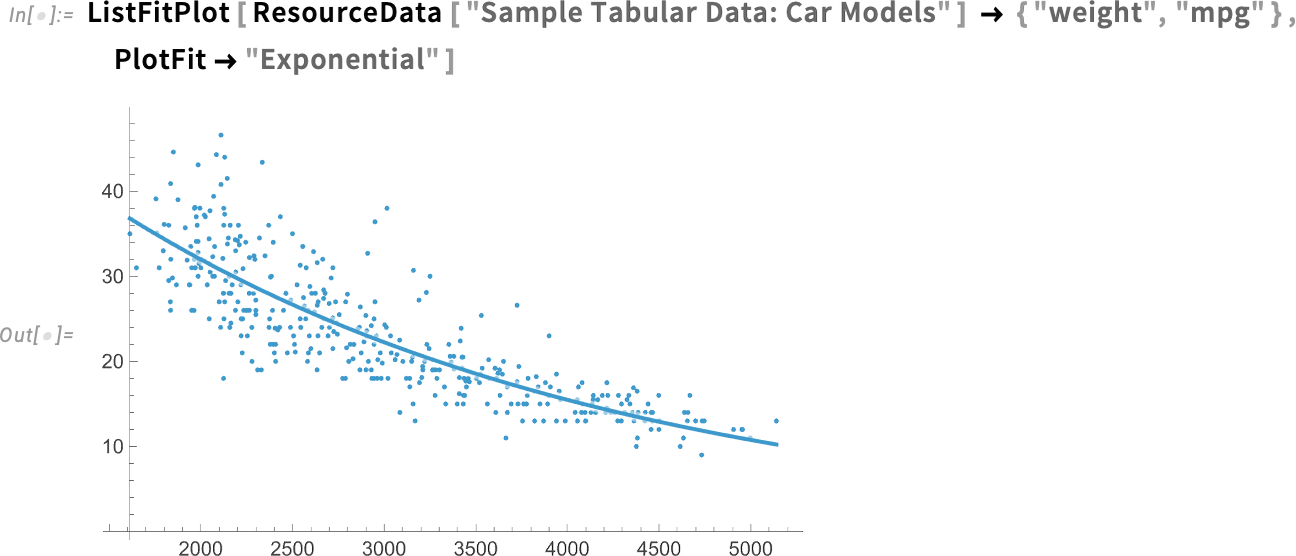
What we’re plotting here are the original data points together with the fit. The option PlotFitElements lets one select exactly what to plot. Like here we’re saying to also plot (95% confidence) band curves:
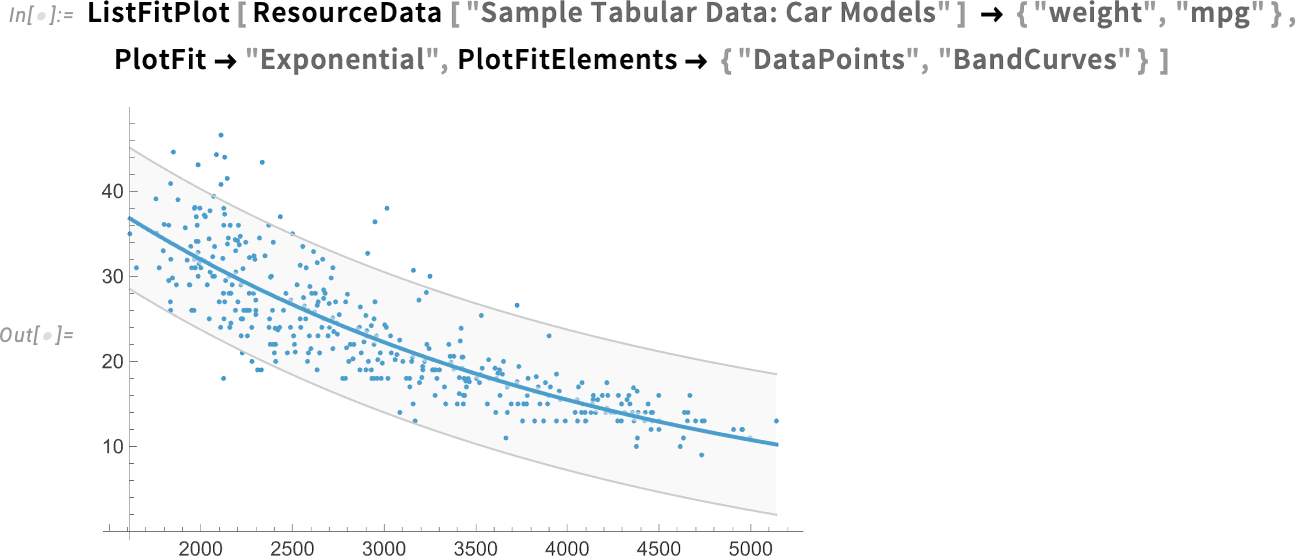
OK, so this is how one can visualize fits. But what about finding out what the fit actually was? Well, actually, we already had functions for doing that, like LinearModelFit and NonlinearModelFit. In Version 14.3, though, there’s also the new LocalModelFit:
Like LinearModelFit etc. what this gives is a symbolic FittedModel object—which we can then, for example, plot:
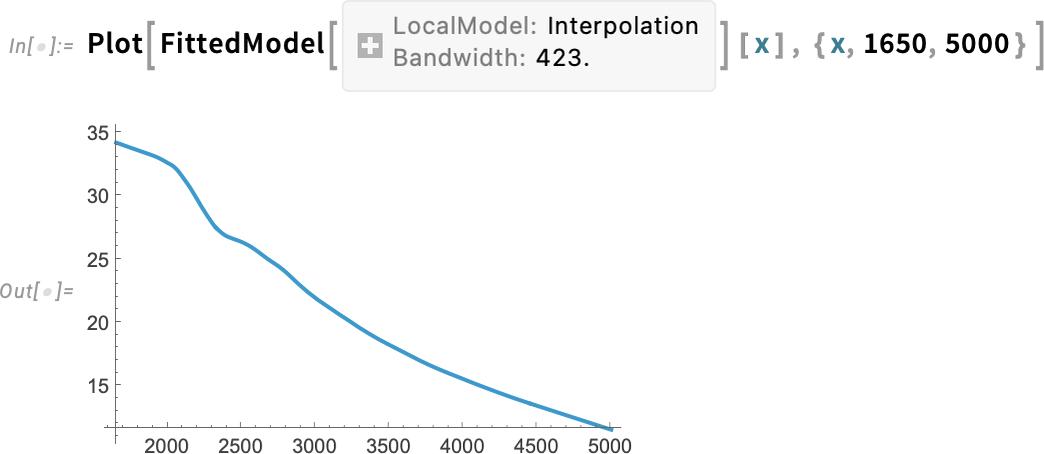
LocalModelFit is a non-parametric fitting function that works by doing local polynomial regressions (LOESS). Another new function in Version 14.3 is KernelModelFit, which fits to sums of basis function kernels:
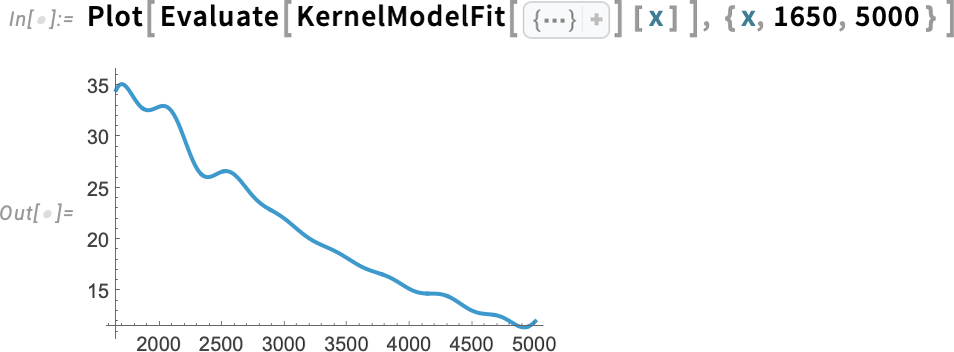
By default the kernels are Gaussian, and the number and width of them is chosen automatically. But here, for example, we’re asking for 20 Cauchy kernels with width 100:

What we just plotted is a best fit curve. But in Version 14.3 whenever we get a FittedModel we can ask not only for the best fit, but also for a fit with errors, represented by Around objects:
We can plot this to show the best fit, along with (95% confidence) band curves:

What this is showing is the best fit, together with the (“statistical”) uncertainty of the fit. Another thing you can do is to show band curves not for the fit, but for all the original data:
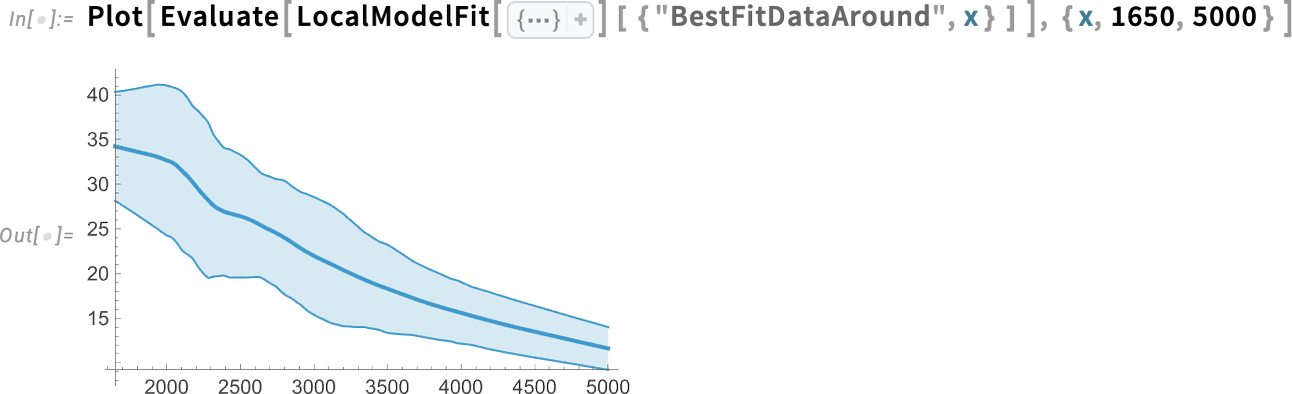
ListFitPlot is specifically set up to generate plots that show fits. As we just saw, you can also get such plots by first explicitly finding fits, and then plotting them. But there’s also another way to get plots that include fits, and that’s by adding the option PlotFit to “ordinary” plotting functions. It’s the very same PlotFit option that you can use in ListFitPlot to specify the type of fit to use. But in a function like ListPlot it specifies to add a fit:
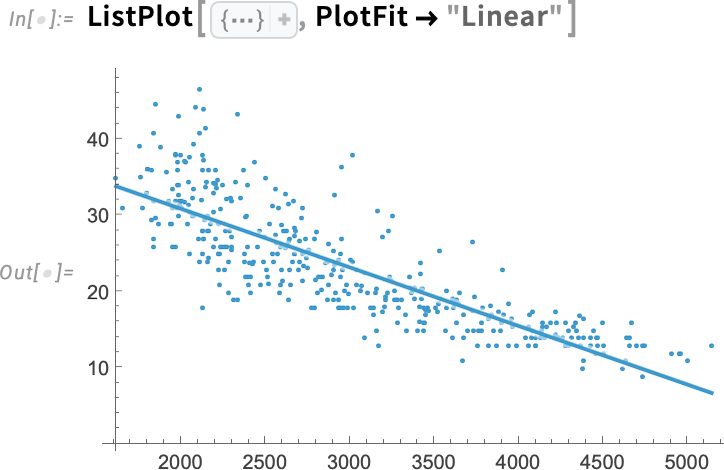
A function like ListLinePlot is set up to “draw a line through data”, and with PlotFit (like with InterpolationOrder) you can tell it “what line”. Here it’s a line based on a local model:

It’s also possible to do fits in 3D. And in Version 14.3, in analogy to ListFitPlot there’s also ListFitPlot3D, which fits a surface to a collection of 3D points:
Here’s what happens if we include confidence band surfaces:

Functions like ListContourPlot also allow fits—and in fact it’s sometimes better to show only the fit for a contour plot. For example, here’s a “raw” contour plot:
And here’s what we get if we plot not the raw data but a local model fit to the data:
The world looks better now. Or, more specifically, in Version 14.3 we’ve updated the styles and rendering we’re using for maps:
Needless to say, this is yet another place where we have to deal with dark mode. Here’s the analogous image in dark mode:
If we look at a smaller area, the “terrain” starts to get faded out:
At the level of a city, roads are made prominent (and they’re rendered in new, crisper colors in Version 14.3):
Zooming in further, we see more details:
And, yes, we can get a satellite image too:
Everything has a dark mode:

An important feature of these maps is that they’re all produced with resolution-independent vector graphics. This was a capability we first introduced as an option in Version 12.2, but in Version 14.3 we’ve managed to make it efficient enough that we’ve now set it as the default.
By the way, in Version 14.3 not only can we render maps in dark mode, we can also get actual night-time satellite images:

We’ve worked hard to pick nice, crisp colors for our default maps. But sometimes you actually want the “base map” to be quite bland, because what you really want to stand out is data you’re plotting on the map. And so that’s what happens by default in functions like GeoListPlot:
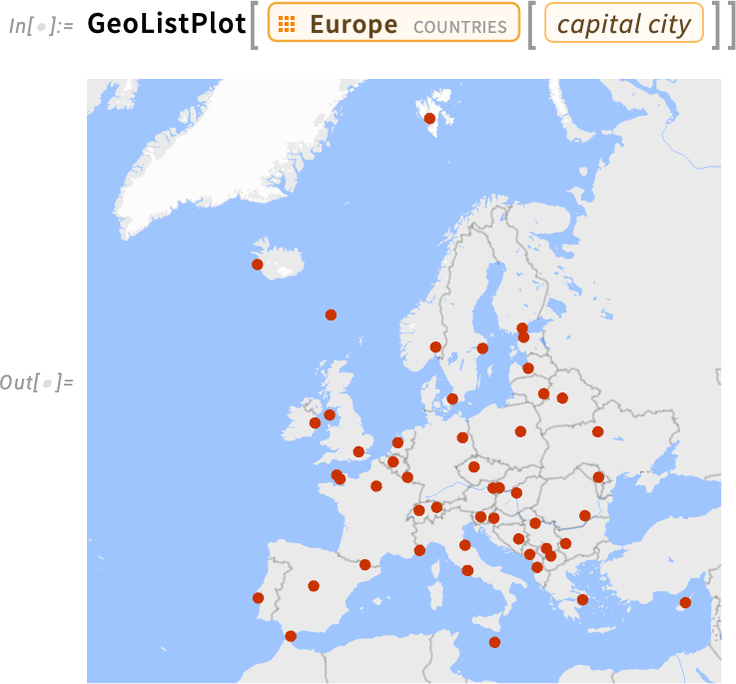
Mapmaking has endless subtleties, some of them mathematically quite complex. Something we finally solved in Version 14.3 is doing true spheroidal geometry on vector geometric data for maps. And a consequence of this is that we can now accurately render (and clip) even very stretched geographic features—like Asia in this projection:
Another new geographic function in Version 14.3 is GeoReposition—which takes a geographic object and transforms its coordinates to move it to a different place on the Earth, preserving its size. So, for example, this shows rather clearly that—with a particular shift and rotation—Africa and South America geometrically fit together (suggesting continental drift):
And, yes, despite its appearance on Mercator projection maps, Greenland is not that big:
And because in the Wolfram Language we always try to make things as general as possible, yes, you can do this “off planet” as well:
“I want to show it in red”, one might say. But what exactly is red? Is it just pure RGBColor[1,0,0], or something slightly different? More than two decades ago we introduced symbols like Red to stand for “pure colors” like RGBColor[1,0,0]. But in making nice-looking, “designed” images, one usually doesn’t want those kinds of “pure colors”. And indeed, a zillion times I’ve found myself wanting to slightly “tweak that red” to make it look better. So in Version 14.3 we’re introducing the new concept of “standard colors”: for example StandardRed is a version of red that “looks red”, but is more “elegant” than “pure red”:

The difference is subtle, but important. For other colors it can be less subtle:
Our new standard colors are picked so that they work well in both light and dark mode:

They also work well not only as foreground colors, but also background colors:


They also are colors that have the same “color weight”, in the sense that—like our default plot colors—they’re balanced in terms of emphasis. Oh, and they’re also selected to go well together.
Here’s an array of all the colors for which we now have symbols (there are White, Black and Transparent as well):

In addition to the “pure colors” and “light colors” which we’ve had for a long time, we’ve not only now added “standard colors”, but also “dark colors”.
So now when you construct graphics, you can immediately get your colors to have a “designer quality” look just by using StandardRed, DarkRed, etc. instead of plain old pure Red.
The whole story of dark mode and light-dark switching introduces yet another issue in the specification of colors. Click any color swatch in a notebook, and you’ll get an interactive color picker:

But in Version 14.3 this color picker has been pretty much completely redesigned, both to handle light and dark modes, and generally to streamline the picking of colors.
Previously you’d by default have to pick colors with sliders:

Now there’s a much-easier-to-use color wheel, together with brightness and opacity sliders:
If you want sliders, then you can ask for those too:
But now you can choose different color spaces—like Hue, which makes the sliders more useful:
What about light-dark switching? Well, the color picker now has this in its right-hand corner:
![]()
Click it, and the color you get will be set up to automatically switch in light and dark mode:
![]()
Selecting either ![]() or
or ![]() you get:
you get:
In other words, in this case, the light mode color was explicitly picked, and the dark mode color was generated automatically.
If you really want to have control over everything, you can use the color space menu for dark mode here, and pick not Automatic, but an explicit color space, and then pick a dark mode color manually in that color space.
And, by the way, as another subtlety, if your notebook was in dark mode, things would be reversed, and you’d instead by default be offered the opportunity to pick the dark mode color, and have the light mode color be generated automatically.
Version 14.2 had all sorts of great new features. But one “little” enhancement that I see—and appreciate—every day is the “spiffing up” that we did of default colors for plots. Just replacing ![]() by
by ![]() ,
, ![]() by
by ![]() ,
, ![]() by
by ![]() , etc. instantly gave our graphics more “zing”, and generally made them look “spiffier”. So now in Version 14.3 we’ve continued this process, “spiffing up” default colors generated by all sorts of functions.
, etc. instantly gave our graphics more “zing”, and generally made them look “spiffier”. So now in Version 14.3 we’ve continued this process, “spiffing up” default colors generated by all sorts of functions.
For example, until Version 14.2 the default colors for DensityPlot were
but now “with more zing” they’re:
Another example—of particular relevance to me, as a longtime explorer of cellular automata—is an update to ArrayPlot. By default, ArrayPlot uses gray levels for successive values (here just 0, 1, 2):

But in Version 14.3, there’s a new option setting—ColorRules![]() "Colors"—that instead uses colors:
"Colors"—that instead uses colors:
And, yes, it also works for larger numbers of values:

As well as in dark mode:

By the way, in Version 14.3 we’ve also improved the handling of meshes—so that they gradually fade out when there are more cells:
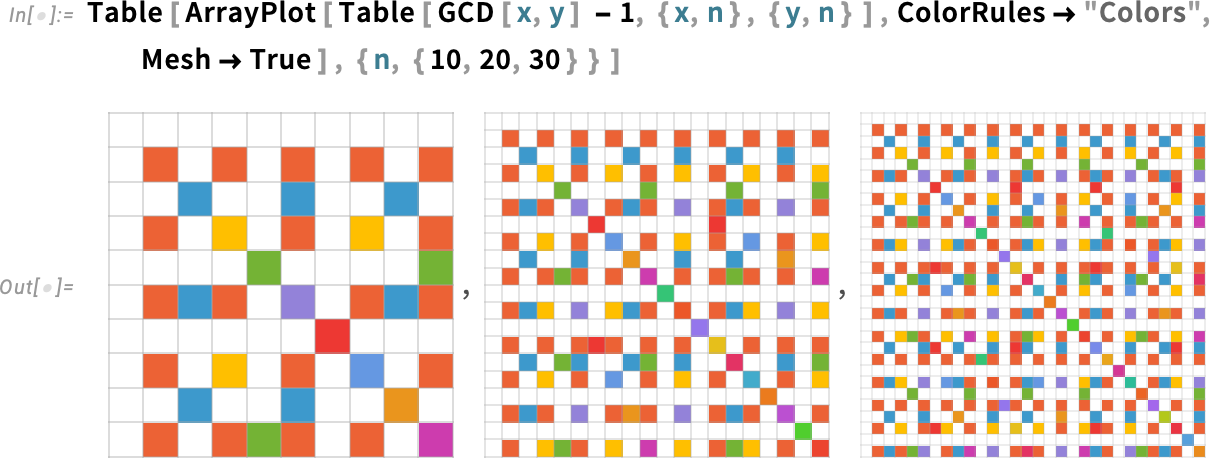
What about 3D? We’ve changed the default even with just 0 and 1 to include a bit of color:

There are updates to colors (and other details of presentation) in many corners of the system. An example is proof objects. In Version 14.2, this was a typical proof object:
Now in Version 14.3 it looks (we think) a bit more elegant:

In addition to colors, another significant update in Version 14.3 has to do with labeling in plots. Here’s a feature space plot of images of country flags:
By default, some of the points are labeled, and some are not. The heuristics that are used try to put labels in empty spaces, and when there aren’t enough (or labels would end up overlapping too much), the labels are just omitted. In Version 14.2 the only choice was whether to have labels at all, or not. But now in Version 14.3 there’s a new option LabelingTarget that specifies what to aim for in adding labels.
For example, with LabelingTarget![]() All, every point is labeled, even if that means there are labels that overlap points, or each other:
All, every point is labeled, even if that means there are labels that overlap points, or each other:

LabelingTarget has a variety of convenient settings. An example is "Dense":

You can also give a number, specifying the fraction of points that should be labeled:
If you want to get into more detail, you can give an association. Like here this specifies that the leaders for all labels should be purely horizontal or vertical, not diagonal:
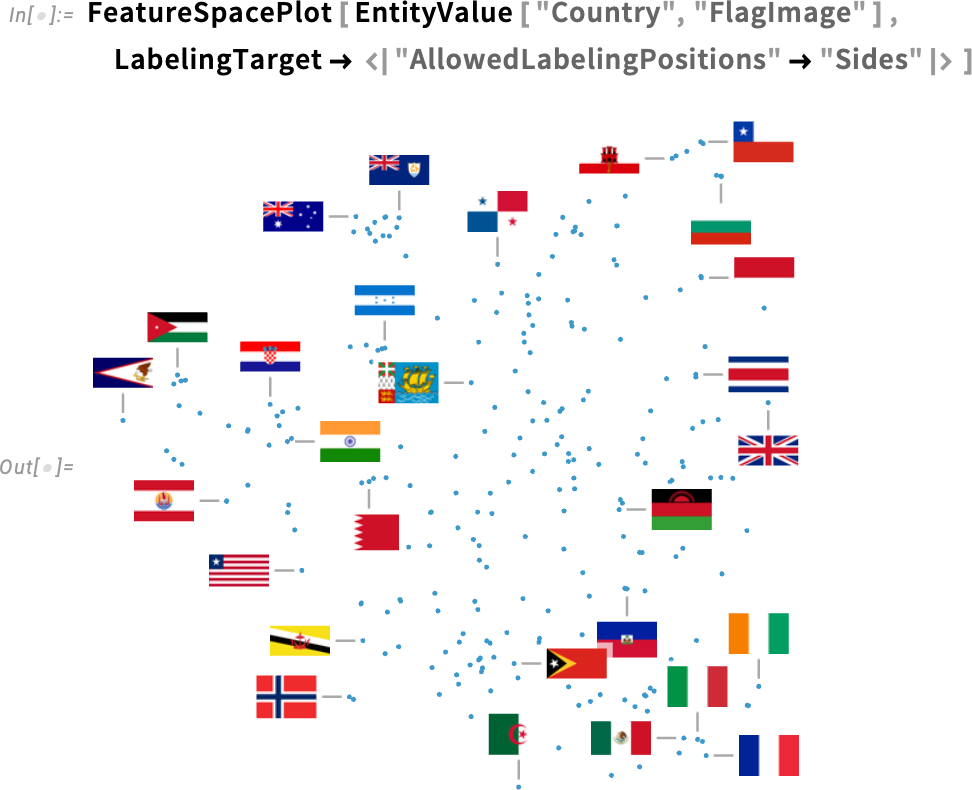
The option LabelingTarget is supported in the full range of visualization functions that deal with points, both in 2D and 3D. Here’s what happens in this case by default:
And here’s what happens if we ask for “20% coverage”:
In Version 14.3 there are all sorts of new upgrades to our visualization capabilities, but there’s also one (very useful) feature that one can think of as a “downgrade”: the option PlotInteractivity that one can use to switch off interactivity in a given plot. For example, with PlotInteractivity![]() False, the bins in a histogram will never “pop” when you mouse over them. And this is useful if you want to ensure efficiency of large and complex graphics, or you’re targeting your graphics for print, etc. where interactivity will never be relevant.
False, the bins in a histogram will never “pop” when you mouse over them. And this is useful if you want to ensure efficiency of large and complex graphics, or you’re targeting your graphics for print, etc. where interactivity will never be relevant.
“Computer algebra” was one of the key features of Version 1.0 all the way back in 1988. Mainly that meant doing operations with polynomials, rational functions, etc.—though of course our general symbolic language always allowed many generalizations to be made. But all the way back in Version 1.0 we had the symbol NonCommutativeMultiply (typed as **) that was intended to represent a “general non-commutative form of multiplication”. When we introduced it, it was basically just a placeholder, and more than anything else, it was “reserved for future expansion”. Well, 37 years later, in Version 14.3, the algorithms are ready, and the future is here! And now you can finally do computation with NonCommutativeMultiply. And the results can be used not only for “general non-commutative multiplication” but also for things like symbolic array simplification, etc.
Ever since Version 1.0 you’ve been able to enter NonCommutativeMultiply as **. And the first obvious change in Version 14.3 is that now ** automatically turns into ⦻. To support math with ⦻ there’s now also GeneralizedPower which represents repeated non-commutative multiplication, and is displayed as a superscript with a tiny ⦻.
OK, so what about doing operations on expressions containing ⦻? In Version 14.3 there’s NonCommutativeExpand:
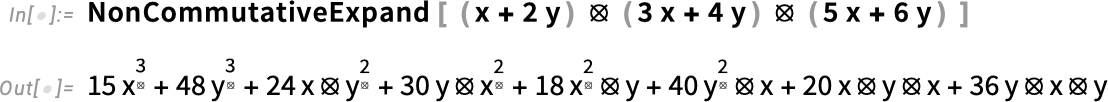
By doing this expansion we’re getting a canonical form for our non-commutative polynomial. In this case, FullSimplify can simplify it
though in general there isn’t a unique “factored” form for non-commutative polynomials, and in some (fairly rare) cases the result can be different from what we started with.
⦻ represents a completely general no-additional-relations form of non-commutative multiplication. But there are many other forms of non-commutative multiplication that are useful. A notable example is . (Dot). In Version 14.2 we introduced ArrayExpand which operates on symbolic arrays:
Now we have NonCommutativeExpand, which can be told to use Dot as its multiplication operation:
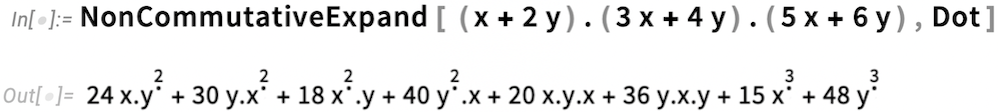
The result looks different, because it’s using GeneralizedPower. But we can use FullSimplify to check the equivalence:
The algorithms we’ve introduced around non-commutative multiplication now allow us to do more powerful symbolic array operations, like this piece of array simplification:
How does it work? Well, at least in multivariate situations, it’s using the non-commutative version of Gröbner bases. Gröbner bases are a core method in ordinary, commutative polynomial computation; in Version 14.3 we’ve generalized them to the non-commutative case:

To get a sense of what kind of thing is going on here, let’s look at a simpler case:
We can think of the input as giving a list of expressions that are assumed to be zero. And by including, for example, a ⦻ b – 1 we’re effectively asserting that a ⦻ b = 1, or, put another way, that b is a right inverse of a. So in effect we’re saying here that b is a right inverse of a, and c is a left inverse. The Gröbner basis that’s output then also includes b – c, showing that the conditions we’ve specified imply that b – c is zero, i.e. that b is equal to c.
Non-commutative algebras show up all over the place, not only in math but also in physics (and particularly quantum physics). They can also be used to represent a symbolic form of functional programming. Like here we’re collecting terms with respect to f, with the multiplication operation being function composition:
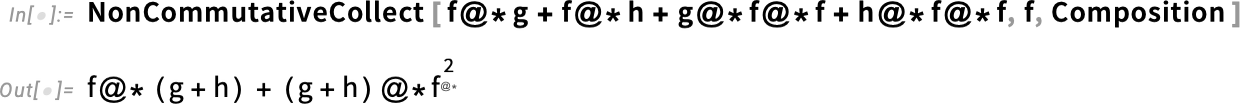
In many applications of non-commutative algebra, it’s useful to have the notion of a commutator:
And, yes, we can check famous commutation relations, like ones from physics:
(There’s AntiCommutator as well.)
A function like NonCommutativeExpand by default assumes that you’re dealing with a non-commutative algebra in which addition is represented by + (Plus), multiplication by ⦻ (NonCommutativeMultiply), and that 0 is the identity for +, and 1 for ⦻. But by giving a second argument, you can tell NonCommutativeExpand that you want to use a different non-commutative algebra. {Dot, n}, for example, represents an algebra of n×n matrices, where the multiplication operation is . (Dot), and the identity is  (SymbolicIdentityArray[n]). TensorProduct represents an algebra of formal tensors, with ⊗ (TensorProduct) as its multiplication operation. But in general you can define your own non-commutative algebra with NonCommutativeAlgebra:
(SymbolicIdentityArray[n]). TensorProduct represents an algebra of formal tensors, with ⊗ (TensorProduct) as its multiplication operation. But in general you can define your own non-commutative algebra with NonCommutativeAlgebra:
Now we can expand an expression assuming it’s an element of this algebra (note the tiny m’s in the generalized “m powers”):

You’ve got a function of x, y, z, and you’ve got a surface embedded in 3D. But how do you plot that function over the surface? Well, in Version 14.3 there’s a function for that:
You can do this over the surface of any kind of region:
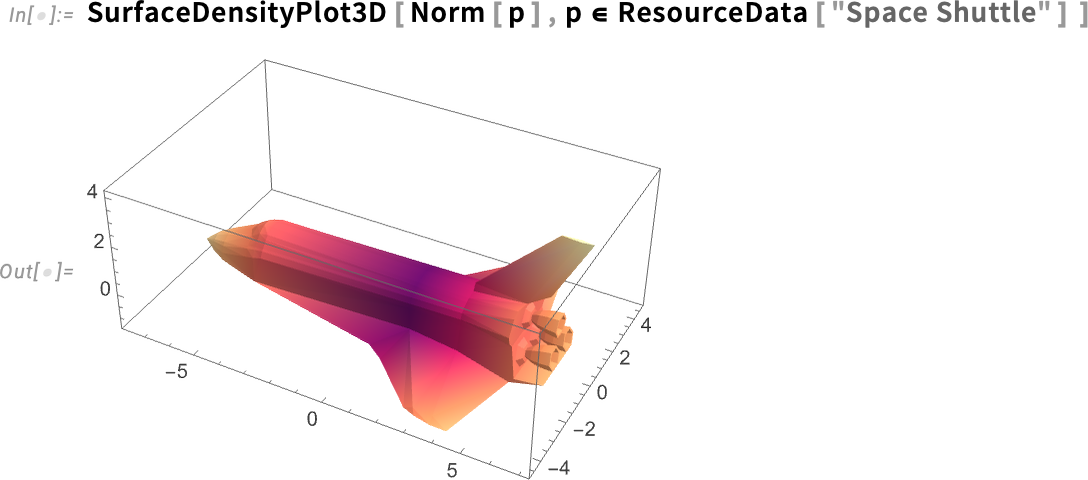
There’s a contour plot version as well:

But what if you don’t want to plot a whole function over a surface, but you just want to highlight some particular aspect of the surface? Then you can use the new function HighlightRegion. You give HighlightRegion your original region, and the region you want to highlight on it. So, for example, this highlights 200 points on the surface of a sphere (and, yes, HighlightRegion correctly makes sure you can see the points, and they don’t get “sliced” by the surface):

Here we’re highlighting a cap on a sphere (specified as the intersection between a ball and the surface of the sphere):

HighlightRegion works not just in 3D but for regions in any number of dimensions:
Coming back to functions on surfaces, another convenient new feature of Version 14.3 is that FunctionInterpolation can now work over arbitrary regions. The goal of FunctionInterpolation is to take some function (which might be slow to compute) and to generate from it an InterpolatingFunction object that approximates the function. Here’s an example where we’re now interpolating a fairly simple function over a complicated region:

Now we can use SurfaceDensityPlot3D to plot the interpolated function over the surface:
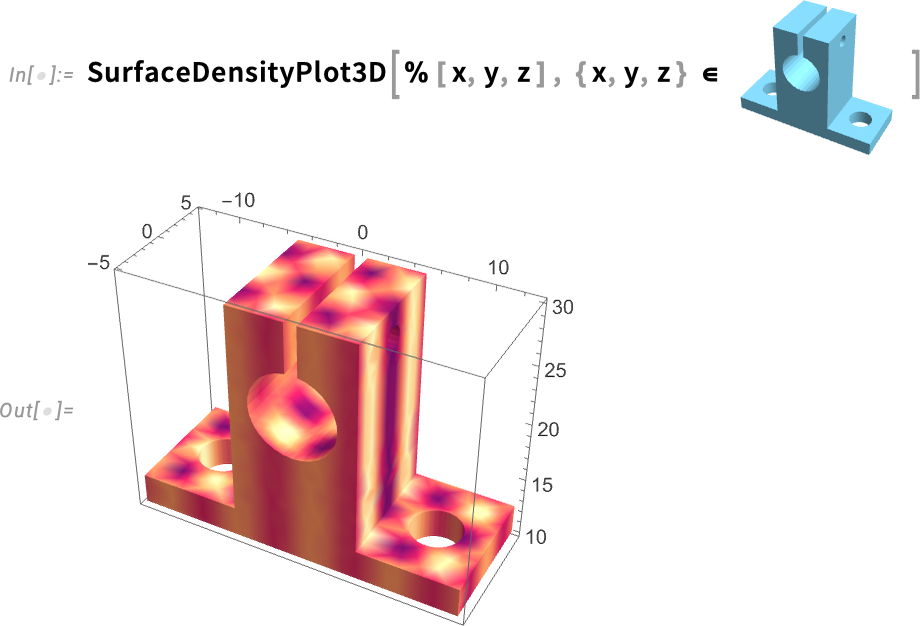
Let’s say we’ve got a 3D object:

In Version 14.3 we can now compute the Gaussian curvature of its surface. Here we’re using the function SurfaceContourPlot3D to plot a value on a surface, with the variable p ranging over the surface:
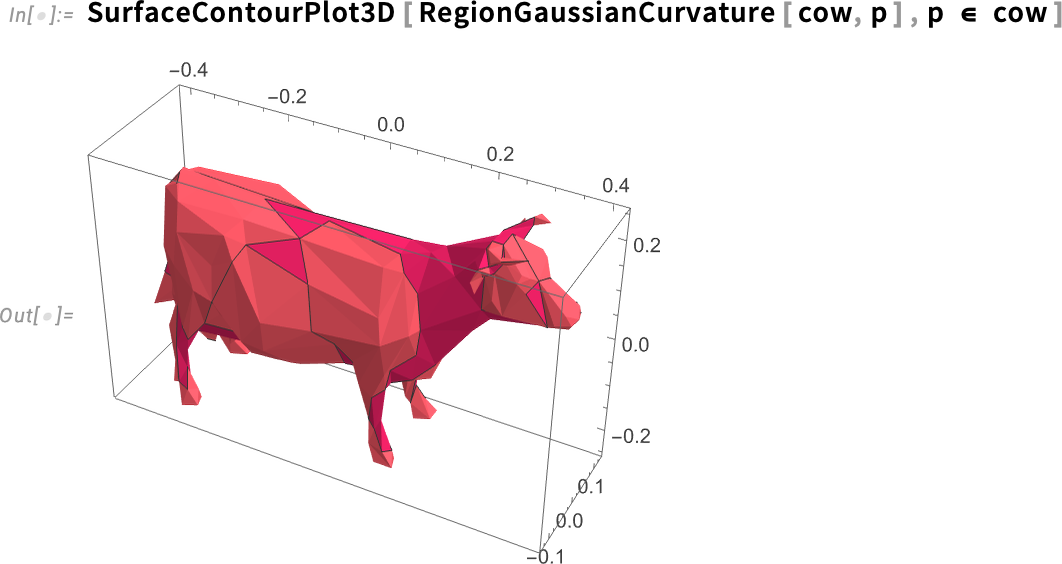
In this example, our 3D object is specified purely by a mesh. But let’s say we have a parametric object:
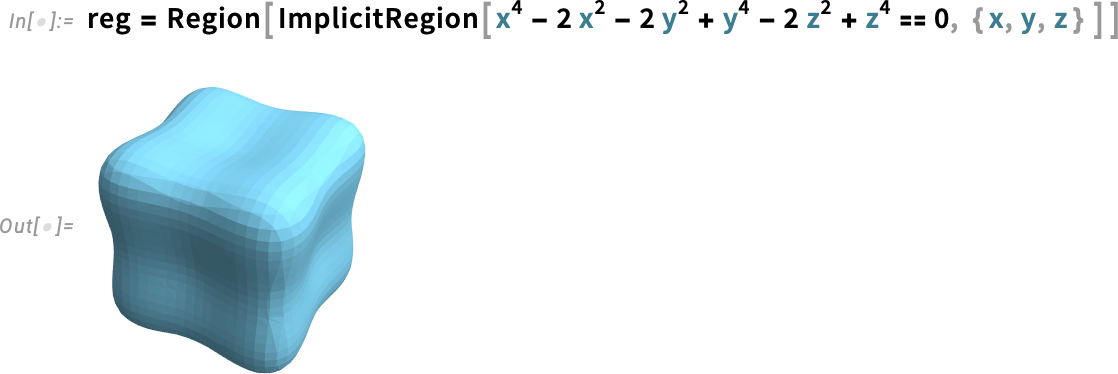
Again we can compute the Gaussian curvature:
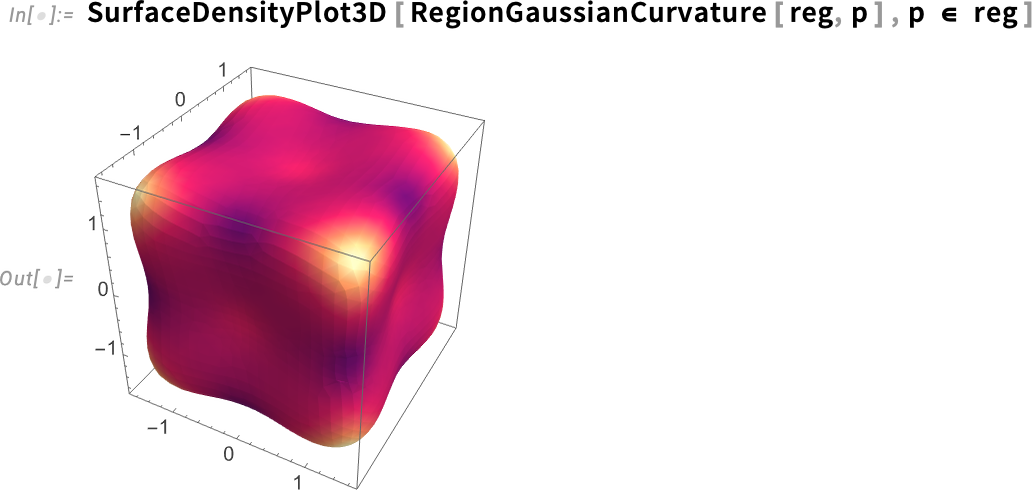
But now we can get exact results. Like this finds a point on the surface:

And this then computes the exact value of the Gaussian curvature at that point:

Version 14.3 also introduces mean curvature measures for surfaces
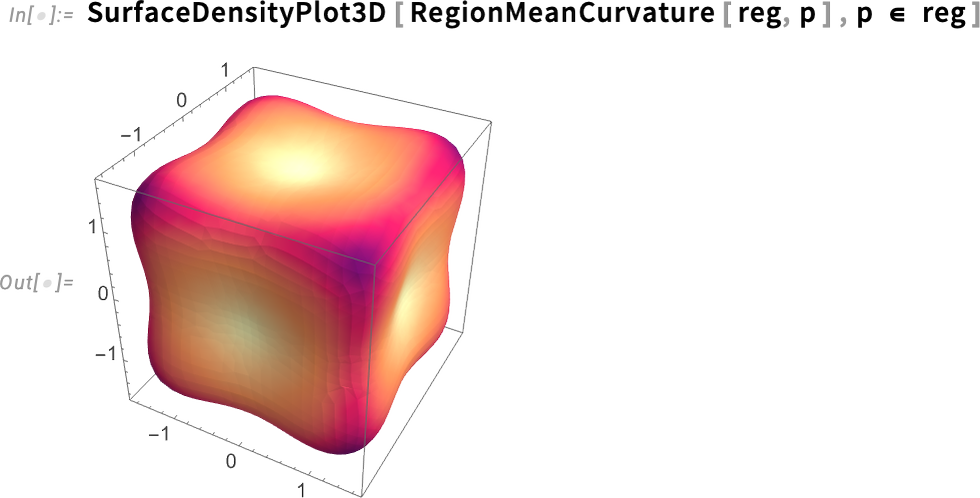
as well as max and min curvatures:
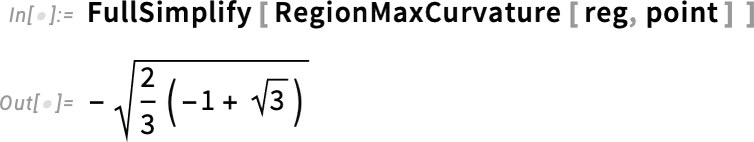
These surface curvatures are in effect 3D generalizations of the ArcCurvature that we introduced more than a decade ago (in Version 10.0): the min and max curvatures correspond to the min and max curvatures of curves laid on the surface; the Gaussian curvature is the product of these, and the mean curvature is their mean.
What’s the shortest path from one point to another—say on a surface? In Version 14.3 you can use FindShortestCurve to find out. As an example, let’s find the shortest path (i.e. geodesic) between two points on a sphere:

Yes, we can see a little arc of what seems like a great circle. But we’d really like to visualize it on the sphere. Well, we can do that with HighlightRegion:
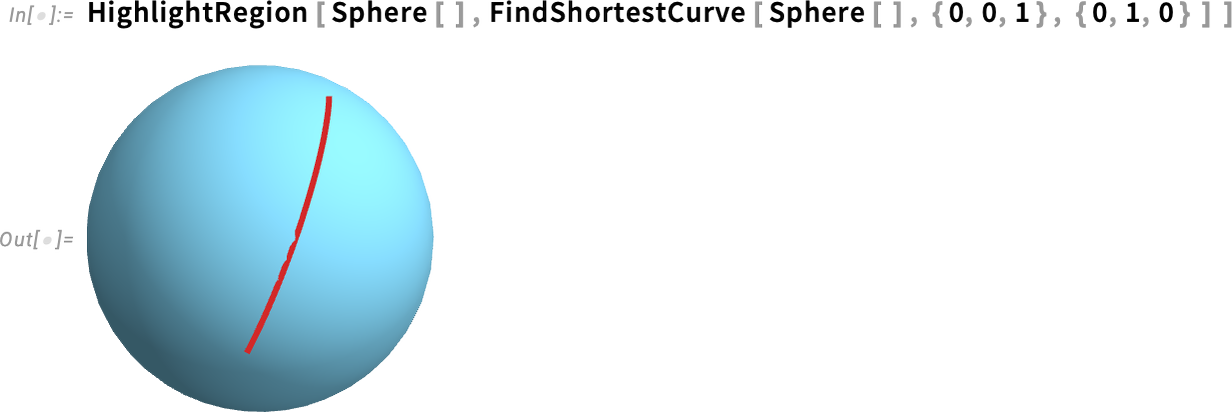
Here’s a similar result for a torus:
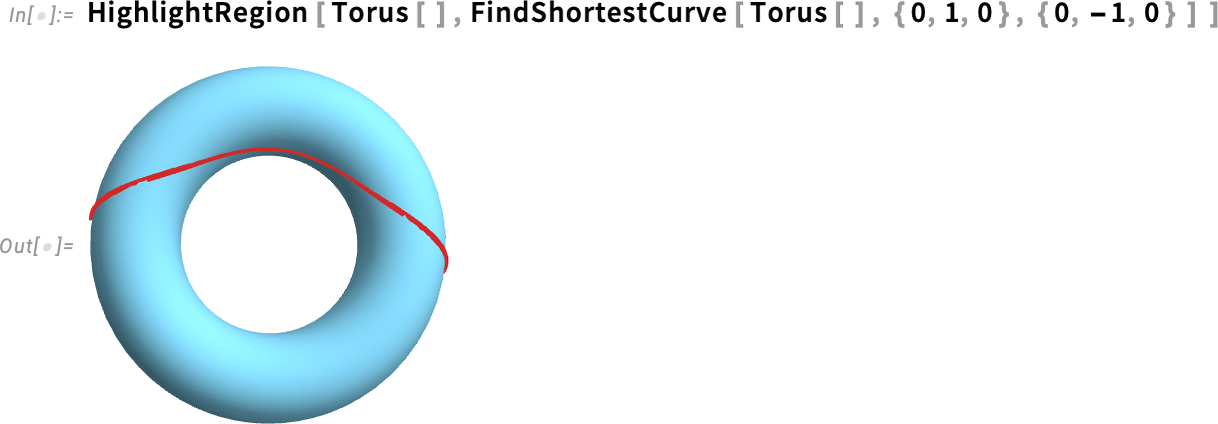
But, actually, any region whatsoever will work. Like, for example, Phobos, a moon of Mars:

Let’s pick two random points on this:
Now we can find the shortest curve between these points on the surface:

You could use ArcLength to find the length of this curve, or you can directly use the new function ShortestCurveDistance:
Here are 25 geodesics between random pairs of points:
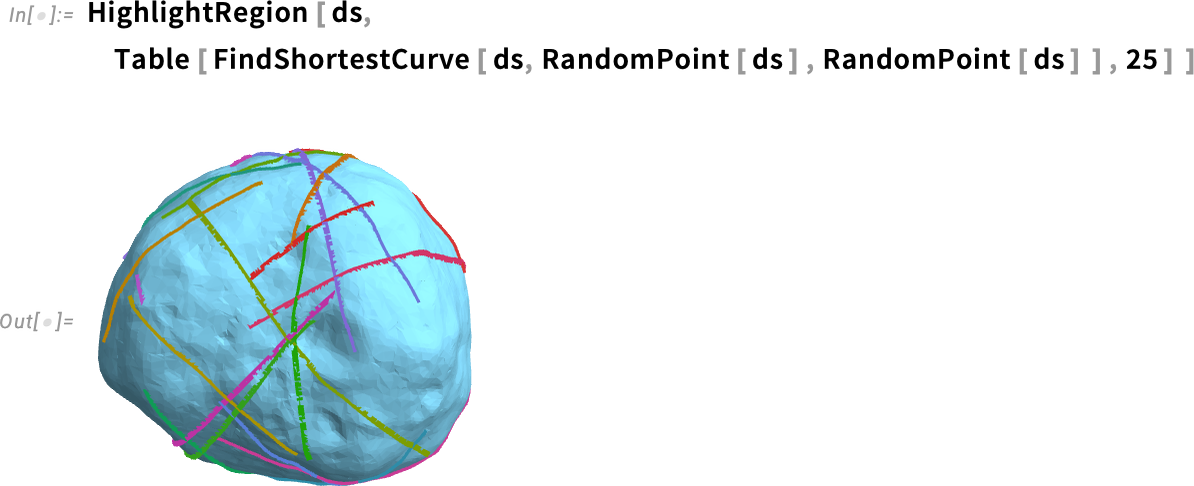
And, yes, the region can be complicated; FindShortestCurve can handle it. But the reason it’s a “Find…” function is that in general there can be many paths of the same length:

We’ve been looking so far at surfaces in 3D. But FindShortestCurve also works in 2D:

So what is this good for? Well, one thing is path planning. Let’s say we’re trying to make a robot get from here to there, avoid obstacles, etc. What is the shortest path it can take? That’s something we can use FindShortestCurve for. And if we want to deal with the “size of the robot” we can do that by “dilating our obstacles”. So, for example, here’s a plan for some furniture:
Let’s now “dilate” this to give the effective region for a robot of radius 0.8:
Inverting this relative to a “rug” now gives us the effective region that the (center of the) robot can move in:
Now we can use FindShortestCurve to find the shortest paths for the robot to get to different places:

Creating “realistic” geometry is hard, particularly in 3D. One way to make it easier is to construct what you want by combining basic shapes (say spheres, cylinders, etc.). And we’ve supported that kind of “constructive geometry” since Version 13.0. But now in Version 14.3, there’s another, powerful alternative: starting with a skeleton of what you want, and then filling it in by taking the limit of an infinite number of subdivisions. So, for example, we might start from a very coarse, faceted approximation to the geometry of a cow, and by doing subdivisions we fill it in to a smooth shape:

It’s pretty typical to start from something “mathematical looking”, and end with something more “natural” or “biological”:

Here’s what happens if we start from a cube, and then do successive steps of subdividing each face:

As a more realistic example, say we start with an approximate mesh for a bone:

SubdivisionRegion immediately gives us a smoothed—and presumably more realistic—version.
Like other computational geometry in the Wolfram Language, SubdivisionRegion works not only in 3D, but also in 2D. So, for example, we can take a random Voronoi mesh
then split it into polygonal cells

and then make subdivision regions from these to produce a rather “pebble look”:
Or in 3D:

Let’s say we have a cloud of 3D points, perhaps from a scanner:
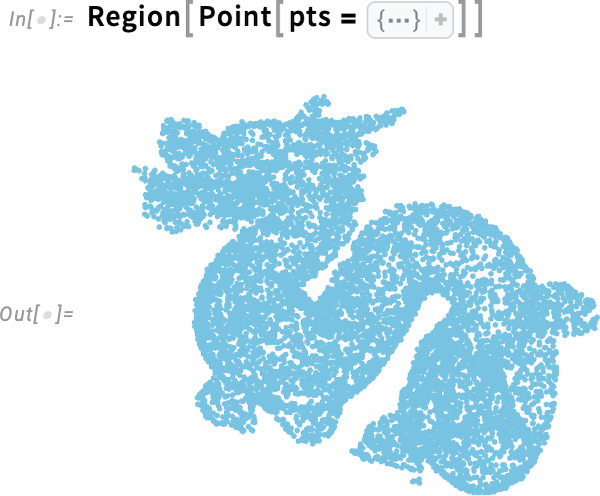
The function ReconstructionMesh introduced in Version 13.1 will attempt to reconstruct a surface from this:

It’s pretty common to see this kind of noisy “crinkling”. But now, in Version 14.3, we have a new function that can smooth this out:

That looks nice. But it has a lot of polygons in it. And for some kinds of computations you’ll want a simpler mesh, with fewer polygons. The new function SimplifyMesh can take any mesh and produce an approximation with fewer polygons:

And, yes, it looks a bit more faceted, but the number of polygons is 10x lower:
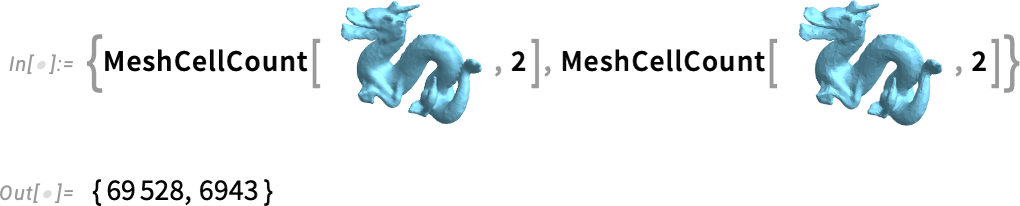
By the way, another new function in Version 14.3 is Remesh. When you do operations on meshes it’s fairly common to generate “weird” (e.g. very pointy) polygons in the mesh. Such polygons can cause trouble if you’re, say, doing 3D printing or finite element analysis. Remesh creates a new “remeshed” mesh in which weird polygons are avoided.
Chemical computation in the Wolfram Language began in earnest six years ago—in Version 12.0—with the introduction of Molecule and many functions around it. And in the years since then we’ve been energetically rounding out the chemistry functionality of the language.
A new capability in Version 14.3 is molecular visualization in which atoms—or bonds—can be colored to show values of a property. So, for example, here are oxidation states of atoms in a caffeine molecule:
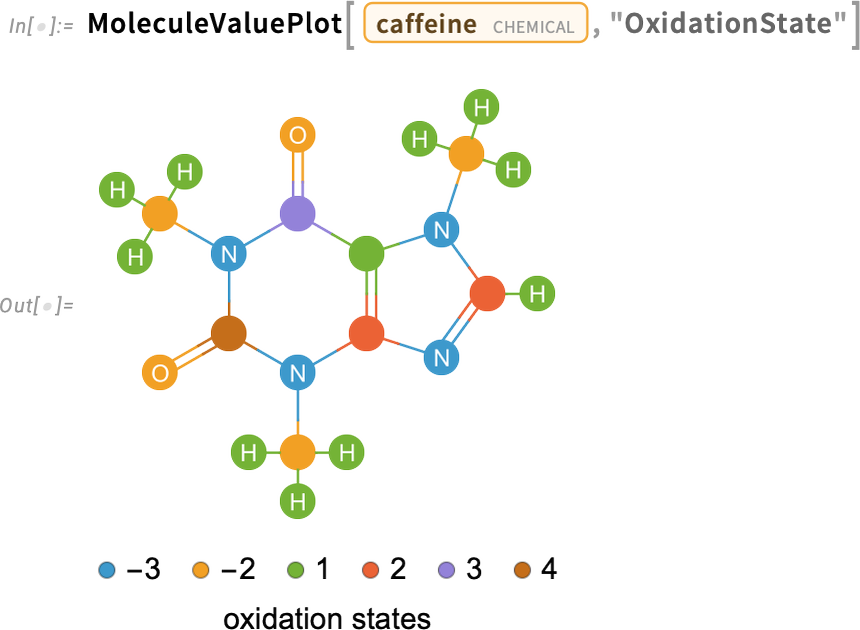
And here’s a 3D version:
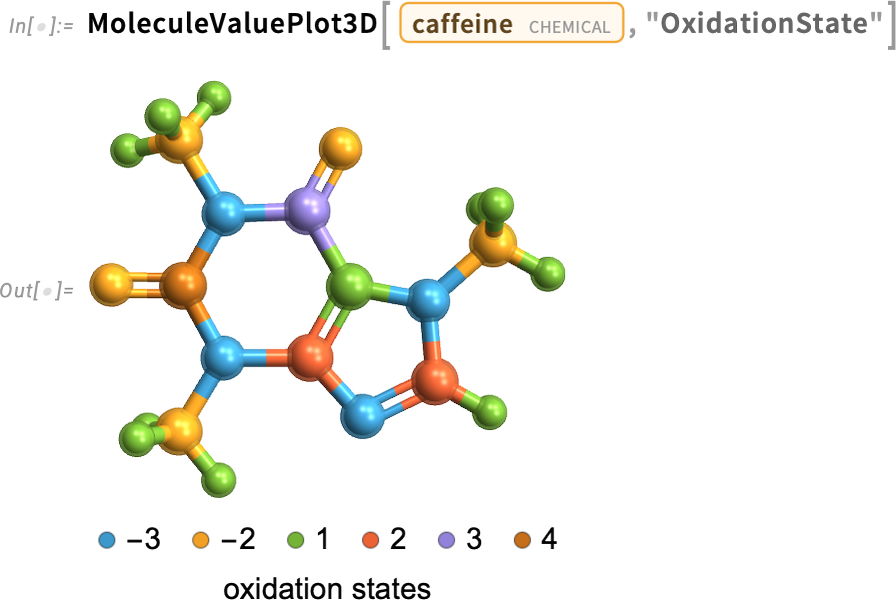
And here’s a case where the quantity we’re using for coloring has a continuous range of values:

Another new chemistry function in Version 14.3 is MoleculeFeatureDistance—which gives a quantitative way to measure “how similar” two molecules are:

You can use this distance in, for example, making a clustering tree of molecules, here of amino acids:

When we first introduced Molecule we also introduced MoleculeModify. And over the years, we’ve been steadily adding more functionality to MoleculeModify. In Version 14.3 we added the ability to invert a molecular structure around an atom, in effect flipping the local stereochemistry of the molecule:

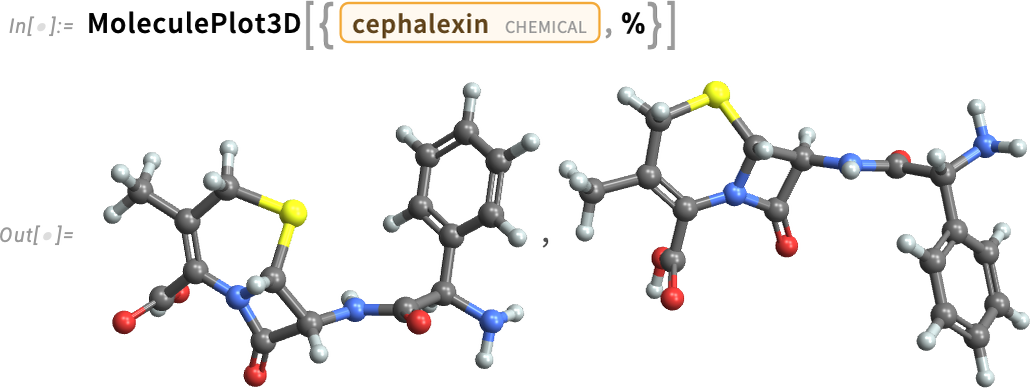
What shape will that protein be? The Wolfram Language has access to a large database of proteins whose structures have been experimentally measured. But what if you’re dealing with a new, different amino acid sequence? How will it fold? Since Version 14.1 BioMolecule has automatically attempted to determine that, but it’s had to call an external API to do so. Now in Version 14.3 we’ve set it up so that you can do the folding locally, on your own computer. The neural net that’s needed is not small—it’s about 11 gigabytes to download, and 30 gigabytes uncompressed on your computer. But being able to work purely locally allows you to systematically do protein folding without the volume and rate limits of an external API.
Here’s an example, doing local folding:

And, remember, this is just a machine-learning-based estimate of the structure. Here’s the experimentally measured structure in this case—qualitatively similar, but not precisely the same:
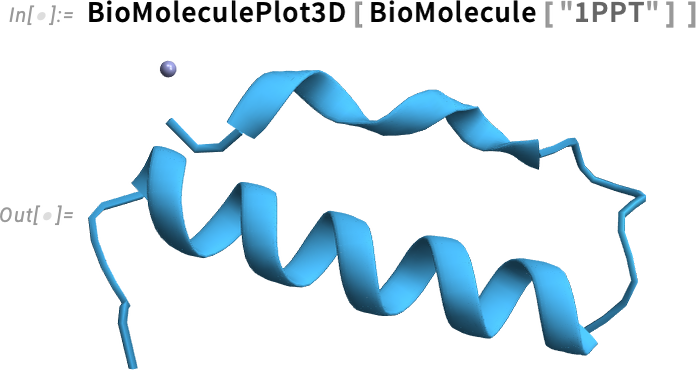
So how can we actually compare these structures? Well, in Version 14.3 there’s a new function BioMoleculeAlign (analogous to MoleculeAlign) that tries to align one biomolecule to another. Here’s our predicted folding again:
Now we align the experimental structure to this:

This now shows the structures together:
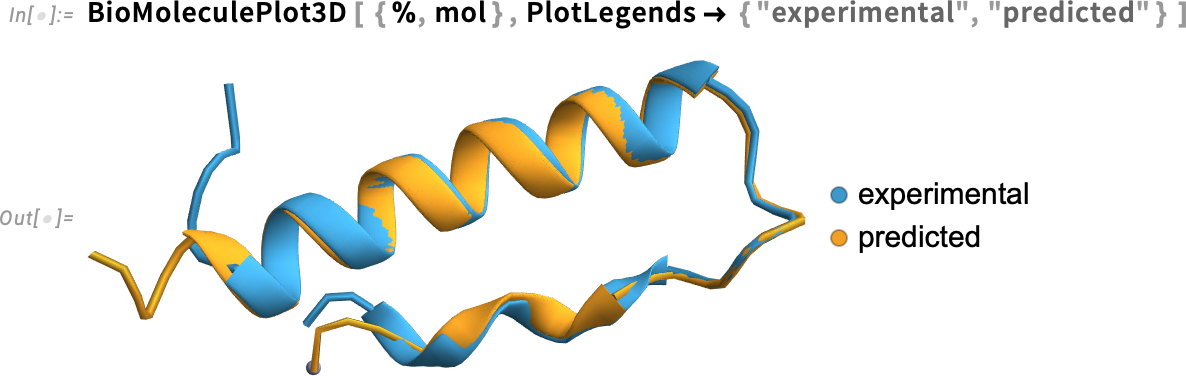
And, yes, at least in this case, the agreement is quite good, and, for example, the error (averaged over core carbon atoms in the backbone) is small:
Version 14.3 also introduces some new quantitative measures of “protein shape”. First, there are Ramachandran angles, which measure the “twisting” of the backbone of the protein (and, yes, those two separated regions correspond to the distinct regions one can see in the protein):
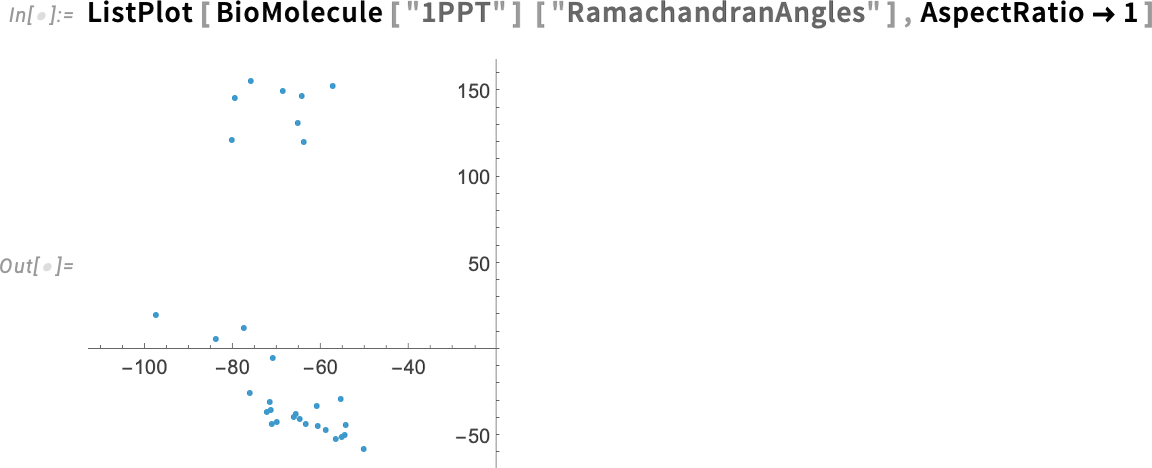
And then there’s the distance matrix between all the residues (i.e. amino acids) in the protein:

For more than a decade Wolfram System Modeler has let one build up and simulate models of real-world engineering and other systems. And by “real world” I mean an expanding range of actual cars, planes, power plants, etc.—with tens of thousands of components—that companies have built (not to mention biomedical systems, etc.) The typical workflow is to interactively construct systems in System Modeler, then to use Wolfram Language to do analysis, algorithmic design, etc. on them. And now, in Version 14.3, we’ve added a major new capability: also being able to validate systems in Wolfram Language.
Will that system stay within the limits that were specified for it? For safety, performance and other reasons, that’s often an important question to ask. And now it’s one you can ask SystemModelValidate to answer. But how do you specify the specifications? Well, that needs some new functions. Like SystemModelAlways—that lets you give a condition that you want the system always to satisfy. Or SystemModelEventually—that lets you give a condition that you want the system eventually to satisfy.
Let’s start with a toy example. Consider this differential equation:
Solve this differential equation and we get:

We can set this up as a System Modeler–style model:

This simulates the system and plots what it does:
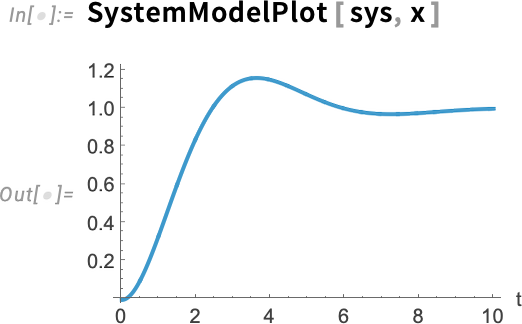
Now let’s say we want to validate the behavior of the system, for example checking whether it ever overshoots value 1.1. Then we just have to say:

And, yes, as the plot shows, the system doesn’t always satisfy this constraint. Here’s where it fails:

And here’s a visual representation of the region of failure:
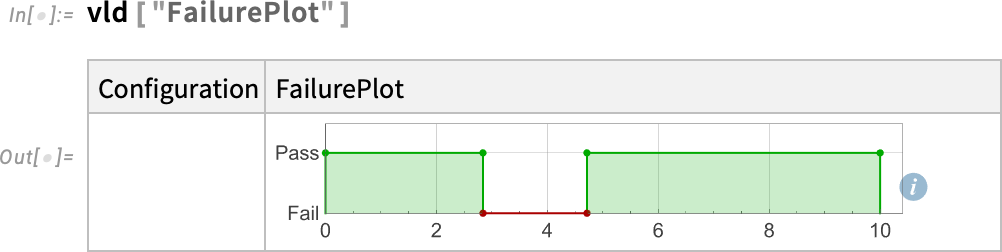
OK, well what about a more realistic example? Here’s a slightly simplified model of the drive train of an electric car (with 469 system variables):
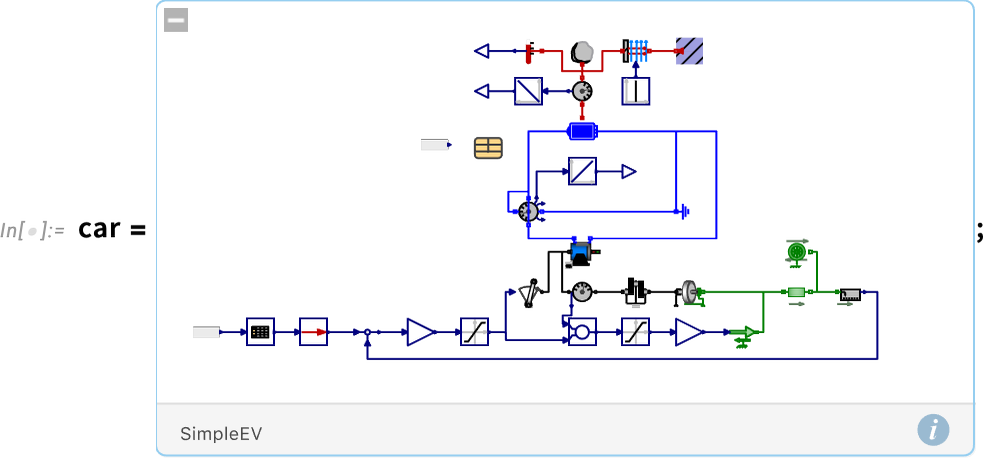
Let’s say we have the specification: “Following the US EPA Highway Fuel Economy Driving Schedule (HWFET) the temperature in the car battery can only be above 301K for at most 10 minutes”. In setting up the model, we already inserted the HWFET “input data”. Now we have to translate the rest of this specification into symbolic form. And for that we need a temporal logic construct, also new in Version 14.3: SystemModelSustain. We end up saying: “Check whether it’s always true that the temperature is not sustained as being above 301 for 10 minutes or more”. And now we can run SystemModelValidate and find out if that’s true for our model:

And no, it’s not. But where does it fail? We can make a plot of that:
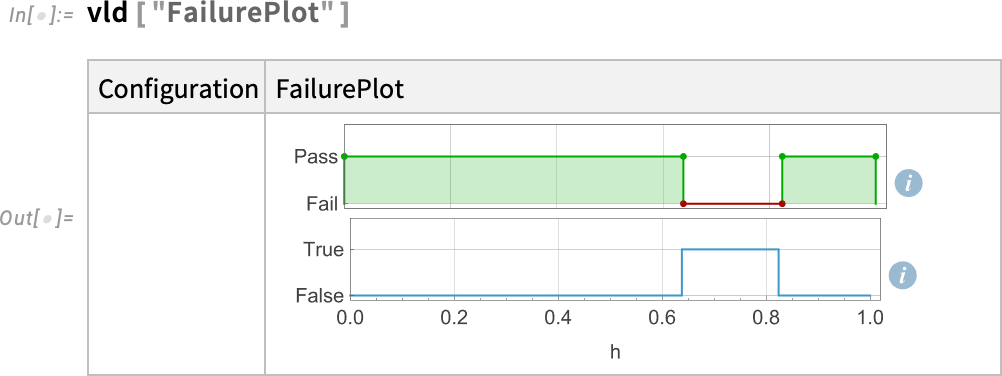
Simulating the underlying model we can see the failure:
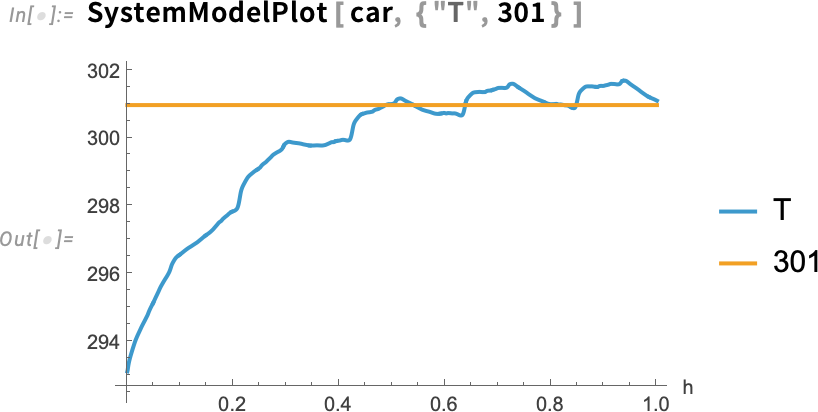
There’s a lot of technology involved here. And it’s all set up to be fully industrial scale, so you can use it on any kind of real-world system for which you have a system model.
It’s a capability we’ve been steadily building for the past 15 years: being able to design and analyze control systems. It’s a complicated area, with many different ways to look at any given control system, and many different kinds of things one wants to do with it. Control system design is also typically a highly iterative process, in which you repeatedly refine a design until all design constraints are satisfied.
In Version 14.3 we’ve made this much easier to do, providing easy access to highly automated tools and to multiple views of your system.
Here’s an example of a model for a system (a “plant model” in the language of control systems), given in nonlinear state space form:

This happens to be a model of an elastic pendulum:

In Version 14.3 you can now click the representation of the model in your notebook, and get a “ribbon” which allows you for example to change the displayed form of the model:
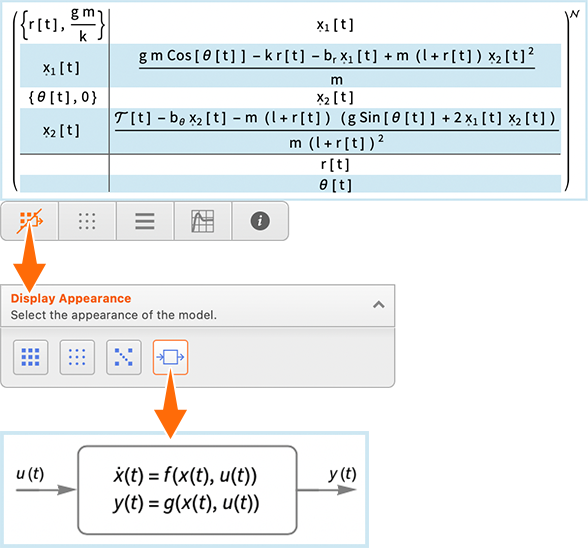
If you’ve filled in numerical values for all the parameters in the model

then you can also immediately do things like get simulation results:
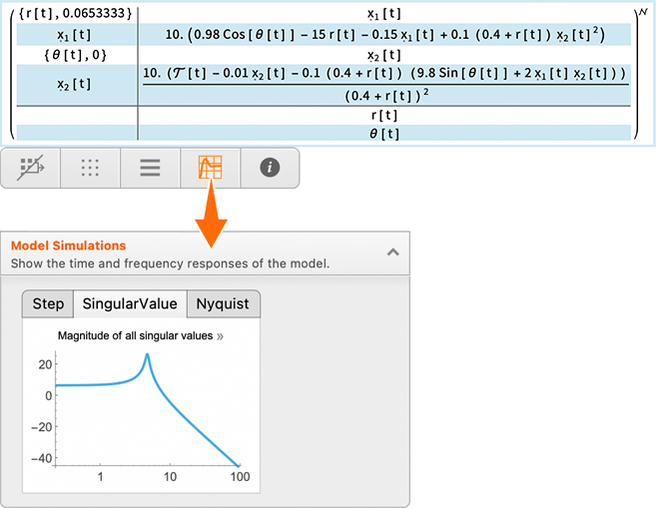
Click the result and you can copy the code to get the result directly:
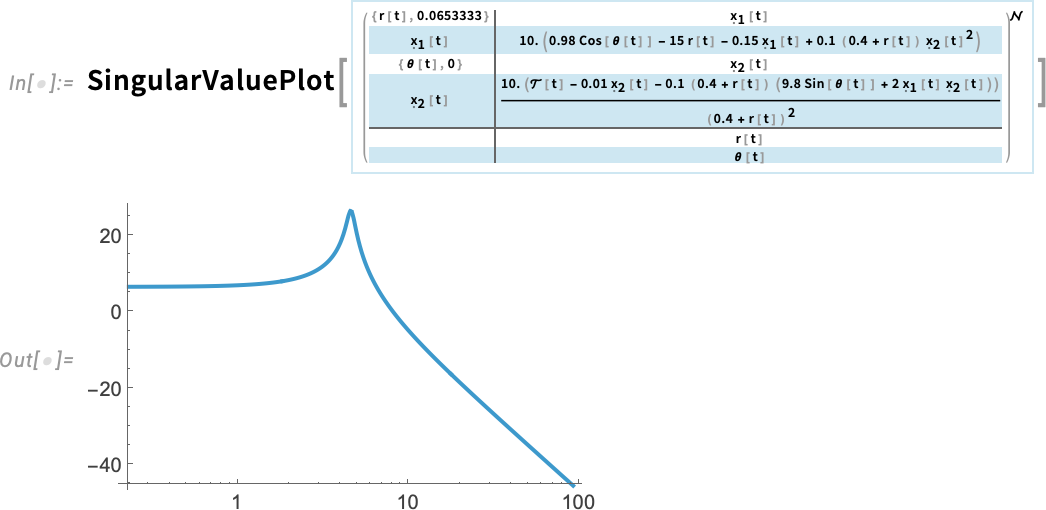
There are lots of properties we can extract from the original state space model. Like here are the differential equations for the system, suitable for input to NDSolve:

As a more industrial example, let’s consider a linearized model for the pitch dynamics of a particular kind of helicopter:

This is the form of the state space model in this case (and it’s linearized around an operating point, so this just gives arrays of coefficients for linear differential equations):
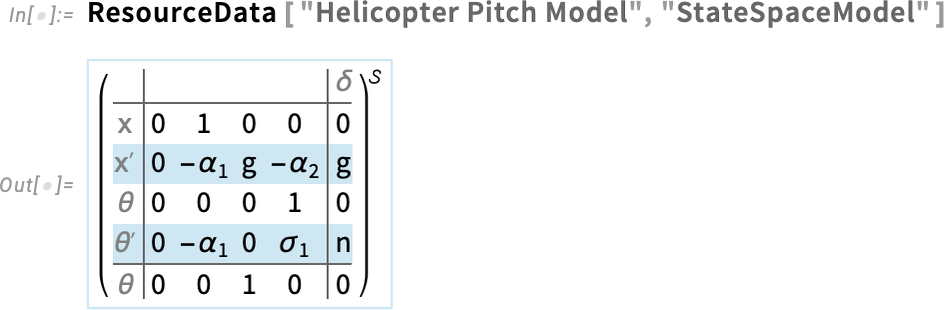
Here’s the model with explicit numerical values filled in:
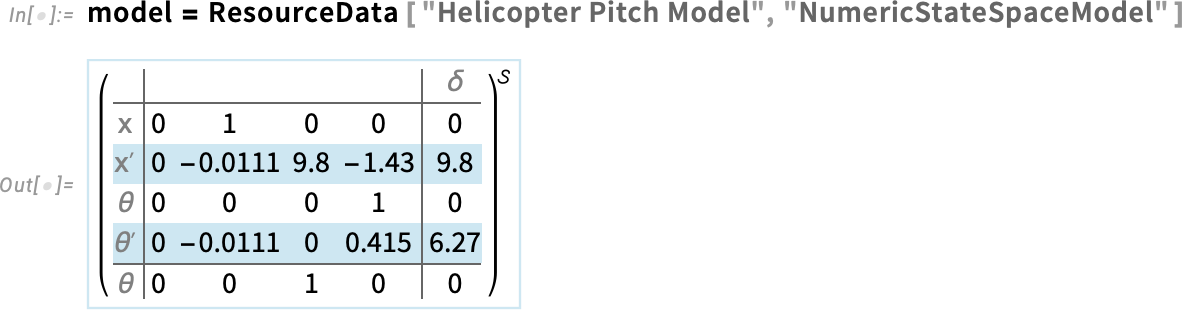
But how does this model behave? To get a quick impression, you can use the new function PoleZeroPlot in Version 14.3, which displays the positions of poles (eigenvalues) and zeros in the complex plane:

If you know about control systems, you’ll immediately notice the poles in the right half-plane—which will tell you that the system as currently set up is unstable.
How can we stabilize it? That’s the typical goal of control system design. As an example here, let’s find an LQ controller for this system—with objectives specified by the “weight matrices” we give here:
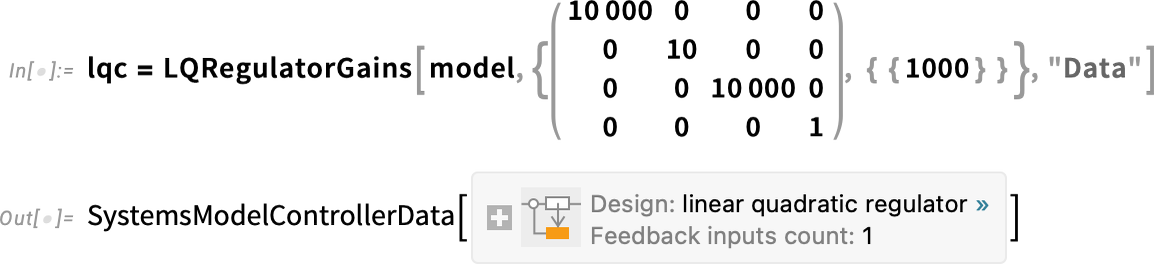
Now we can plot (in orange) the poles for the system with this controller in the loop—together with (in blue) the poles for the original uncontrolled system:
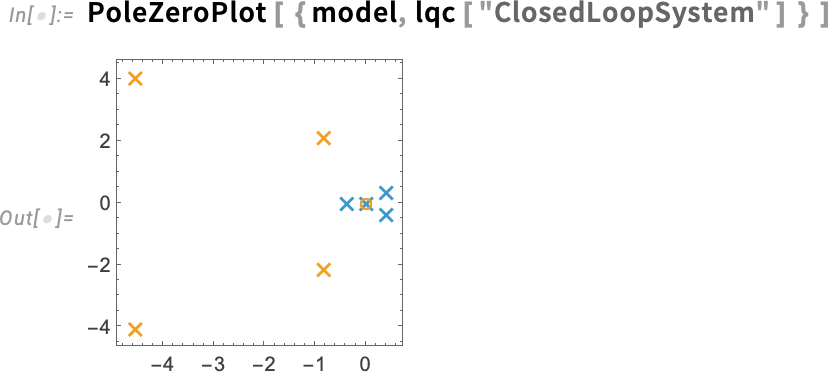
And we see that, yes, the controller we computed does indeed make our system stable.
So what does the system actually do? We can ask for its response given certain initial conditions (here that the helicopter is slightly tipped up):

Plotting this we see that, yes, the helicopter wiggles a bit, then settles down:

How should you lay out a tree? In fairly small cases it’s feasible to have it look like a (botanical) tree, albeit with its root at the top:
For larger cases, it’s not so clear what to do. Our default is just to fall through to general graph layout techniques:
But in Version 14.3 there’s something more elegant we can do: effectively lay the graph out in hyperbolic space:
In "HyperbolicRadialEmbedding" we’re in effect having every branch of the tree go out radially in hyperbolic space. But in general we might just want to operate in hyperbolic space, while treating graph edges like springs. Here’s an example of what happens in this case:

At a mathematical level, hyperbolic space is infinite. But in doing our layouts, we’re projecting it into a “Poincaré disk” coordinate system. In general, one needs to pick the origin of that coordinate system, or in effect the “root vertex” for the graph, that will be rendered at the center of the Poincaré disk:

We’ve done Laplace. Fourier. Mellin. Hankel. Radon. All these are integral transforms. And now in Version 14.3 we’re on to the very last (and most difficult) of the common types of integral transforms: Hilbert transforms. Hilbert transforms show up a lot when one’s dealing with signals and things like them. Because with the right setup, a Hilbert transform basically takes the real part of a signal, say as a function of frequency, and—assuming one’s dealing with a well-behaved analytic function—gives one its imaginary part.
A classic example (in optics, scattering theory, etc.) is:

Needless to say, our HilbertTransform can do essentially any Hilbert transform that can be done symbolically:
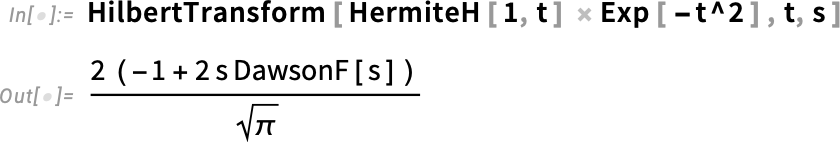
And, yes, this produces a somewhat exotic special function, that we added in Version 7.0.
And talking of special functions, like many versions, Version 14.3 adds yet more special functions. And, yes, after nearly four decades we’re definitely running out of special functions to add, at least in the univariate case. But in Version 14.3 we’ve got just one more set: Lommel functions. The Lommel functions are solutions to the inhomogeneous Bessel differential equation:
They come in four varieties—LommelS1, LommelS2, LommelT1 and LommelT2:
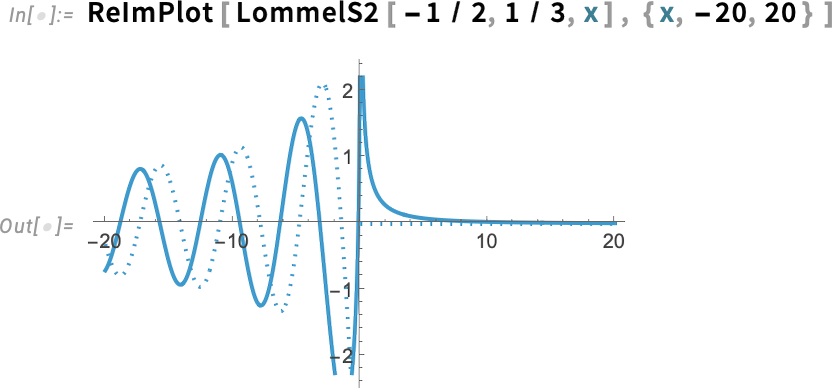
And, yes, we can evaluate them (to any precision) anywhere in the complex plane:
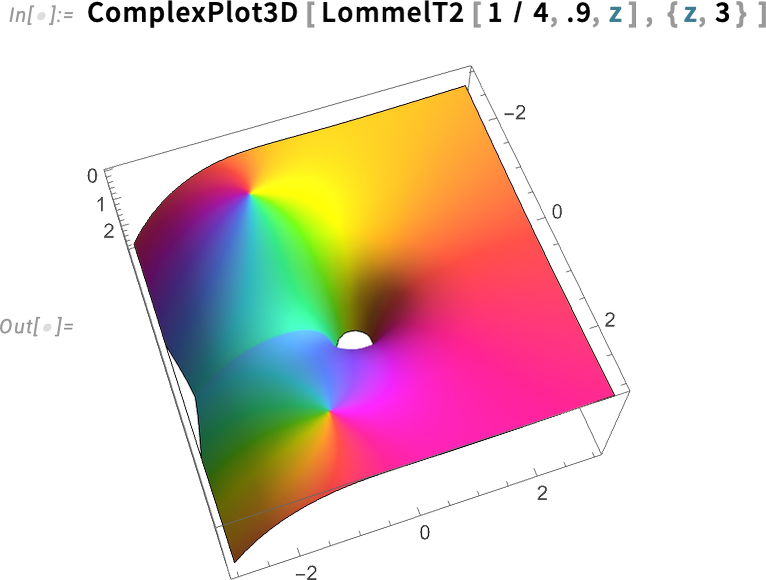
There are all sorts of relations between Lommel functions and other special functions:
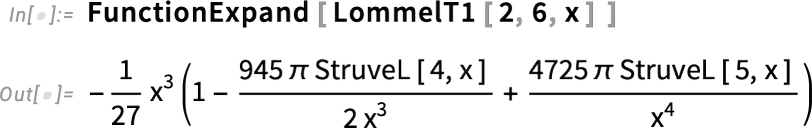
And, yes, like with all our other special functions, we’ve made sure that Lommel functions work throughout the system:
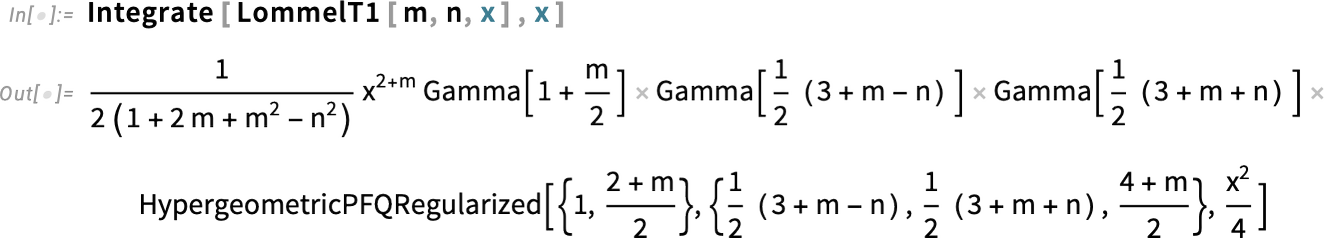
Matrices show up everywhere. And starting with Version 1.0 we’ve had all sorts of capabilities for powerfully dealing with them—both numerically and symbolically. But—a bit like with special functions—there are always more corners to explore. And starting with Version 14.3 we’re making a push to extend and streamline everything we do with matrices.
Here’s a rather straightforward thing. Already in Version 1.0 we had NullSpace. And now in Version 14.3 we’re adding RangeSpace to provide a complementary representation of subspaces. So, for example, here’s the 1-dimensional null space for a matrix:
And here is the corresponding 2 (= 3 – 1)-dimensional range space for the same matrix:
What if you want to project a vector onto this subspace? In Version 14.3 we’ve extended Projection to allow you to project not just onto a vector but onto a subspace:
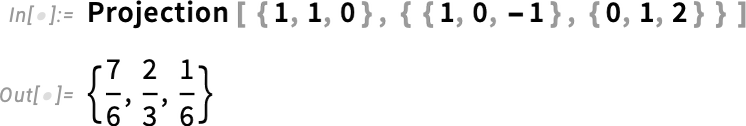
All these functions work not only numerically but also (using different methods) symbolically:
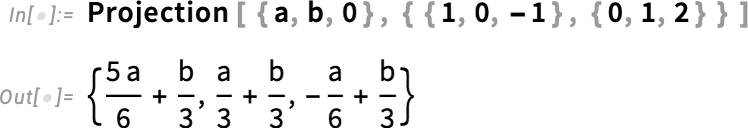
A meatier set of new capabilities concern decompositions for matrices. The basic concept of a matrix decomposition is to pick out the core operation that’s needed for a certain class of applications of matrices. We had a number of matrix decompositions even in Version 1.0, and over the years we’ve added several more. And now in Version 14.3, we’re adding four new matrix decompositions.
The first is EigenvalueDecomposition, which is essentially a repackaging of matrix eigenvalues and eigenvectors set up to define a similarity transform that diagonalizes the matrix:
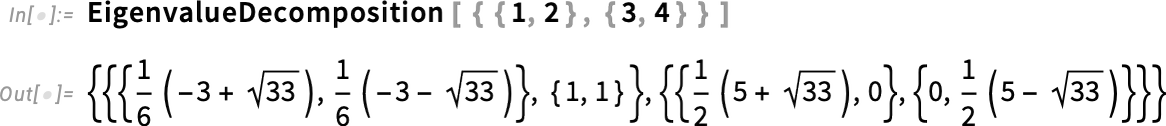
The next new matrix decomposition in Version 14.3 is FrobeniusDecomposition:
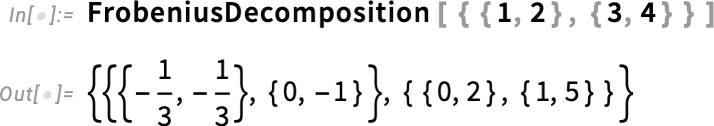
Frobenius decomposition is essentially achieving the same objective as eigenvalue decomposition, but in a more robust way that, for example, doesn’t get derailed by degeneracies, and avoids generating complicated algebraic numbers from integer matrices.
In Version 14.3 we’re also adding a couple of simple matrix generators convenient for use with functions like FrobeniusDecomposition:
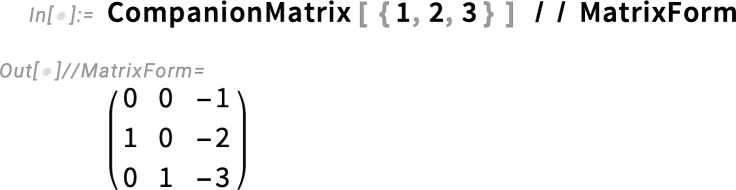
Another set of new functions in effect mix matrices and (univariate) polynomials. For a long time we’ve had:
Now we’re adding MatrixMinimalPolynomial:
We’re also adding MatrixPolynomialValue—which is a kind of polynomial special case of MatrixFunction—and which computes the (matrix) value of a polynomial when the variable (say m) takes on a matrix value:

And, yes, this shows that—as the Cayley–Hamilton theorem says—our matrix satisfies its own characteristic equation.
In Version 6.0 we introduced HermiteDecomposition for integer matrices. Now in Version 14.3 we’re adding a version for polynomial matrices—that uses PolynomialGCD instead of GCD in its elimination process:
Sometimes, though, you don’t want to compute full decompositions; you only want the reduced form. So in Version 14.3 we’re adding the separate reduction functions HermiteReduce and PolynomialHermiteReduce (as well as SmithReduce):
One more thing that’s new with matrices in Version 14.3 is some additional notation—particularly convenient for writing out symbolic matrix expressions. An example is the new StandardForm version of Norm:
We had used this in TraditionalForm before; now it’s in StandardForm as well. And you can enter it by filling in the template you get by typing ESCnormESC. Some of the other notations we’ve added are:
In every version—for the past 37 years—we’ve been continuing to tune up details of Wolfram Language design (all the while maintaining compatibility). Version 14.3 is no exception.
Here’s something that I’ve wanted for many, many years—but it’s been technically difficult to implement, and only now become possible: multi-argument With.
I often find myself nesting With constructs:
But why can’t one just flatten this out into a single multi-argument With? Well, in Version 14.3 one now can:
Like the nested With, this first replaces x by 1, then replaces y by x + 1. If both replacements are done “in parallel”, y gets the original, symbolic x, not the replaced one:
How could one have told the difference? Look carefully at the syntax coloring. In the multi-argument case, the x in y = x + 1 is green, indicating that it’s a scoped variable; in the non-multi-argument case, it’s blue, indicating that it’s a global variable.
As it turns out, syntax coloring is one of the tricky issues in implementing multi-argument With. And you’ll notice that as you add arguments, variables will appropriately turn green to indicate that they’re scoped. In addition, if there are conflicts between variables, they’ll turn red:
What’s the 5th element of a 3-element list? One might just say it’s an error. But an alternative is to treat the list as cyclic. And that’s what the new Cyclic function in Version 14.3 does:
You can think of Cyclic[{a,b,c}] as representing an infinite sequence of repetitions of {a,b,c}. This just gives the first part of {a,b,c}:
But this “wraps around”, and gives the last part of {a,b,c}:
You can pick out any “cyclic element”; you’re always just picking out the element mod the length of the block of elements you specify:
Cyclic provides a way to do computations with effectively infinite repeating lists. But it’s also useful in less “computational” settings, like in specifying cyclic styling, say in Grid:

Version 14.2 introduced game-changing capabilities for handling gigabyte-sized tabular data, centered around the new function Tabular. Now in Version 14.3 we’re rounding out the capabilities of Tabular in several areas.
The first has to do with where you can import data for Tabular from. In addition to local files and URLs, Version 14.2 supported Amazon S3, Azure blob storage, Dropbox and IPFS. In Version 14.3 we’re adding OneDrive and Kaggle. We’re also adding the capability to “gulp in” data from relational databases. Already in Version 14.2 we allowed the very powerful possibility of handling data “out of core” in relational databases through Tabular. Now in Version 14.3 we’re adding the capability to directly import for in-core processing the results of queries from such relational databases as SQLite, Postgres, MySQL, SQL Server and Oracle. All this works through DataConnectionObject, which provides a symbolic representation of an active data connection, and which handles such issues as authentication.
Here’s an example of a data connection object that represents the results of a particular query on a sample database:
Import can take this and resolve it to an (in-core) Tabular:

One frequent source of large amounts of tabular data is log files. And in Version 14.3 we’re adding highly efficient importing of Apache log files to Tabular objects. We’re also adding new import capabilities for Common Log and Extended Log files, as well as import (and export) for JSON Lines files:

In addition, we’re adding the capabilities to import as Tabular objects for several other formats (MDB, DBF, NDK, TLE, MTP, GPX, BDF, EDF). Another new feature in Version 14.3 (used for example for GPX data) is a “GeoPosition” column type.
As well as providing new ways to get data into Tabular, Version 14.3 expands our capabilities for manipulating tabular data, and in particular for combining data from multiple Tabular objects. One new function that does this is ColumnwiseCombine. The basic idea of ColumnwiseCombine is to take multiple Tabular objects and to look at all possible combinations of rows in these objects, then to create a single new Tabular object that contains those combined rows that satisfy some specified condition.
Consider these three Tabular objects:
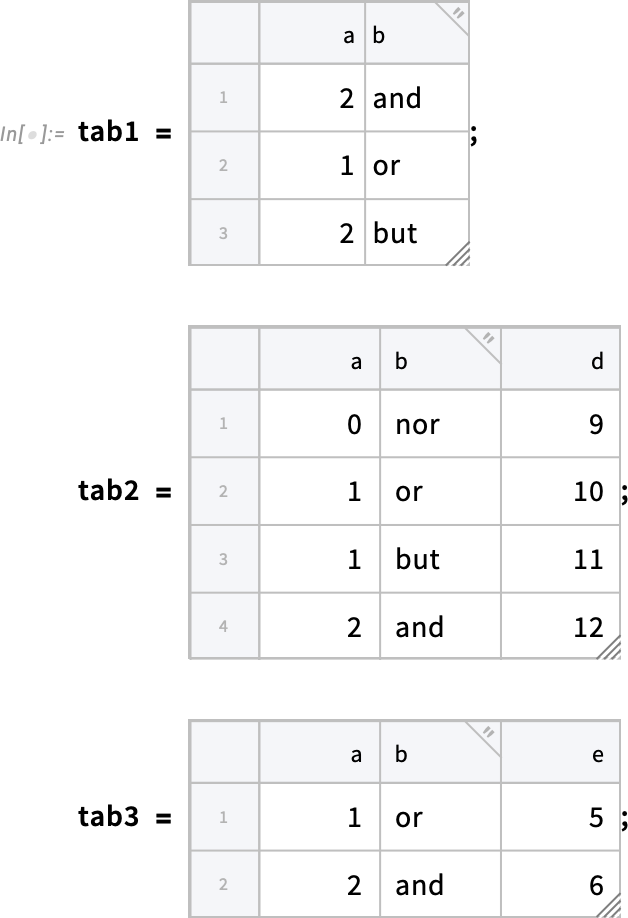
Here’s an example of ColumnwiseCombine in which the criterion for including a combined row is that the values in columns "a" and "b" agree between the different instances of the row that are being combined:

There are lots of subtle issues that can come up. Here we’re doing an “outer” combination, in which we’re effectively assuming that an element that’s missing from a row matches our criterion (and we’re then including rows with those explicit “missing elements” added):

Here’s another subtlety. If in different Tabular objects there are columns that have the same name, how does one distinguish elements from those different Tabular objects? Here we’re effectively giving each Tabular a name, which is then used to form an extended key in the resulting combined Tabular:
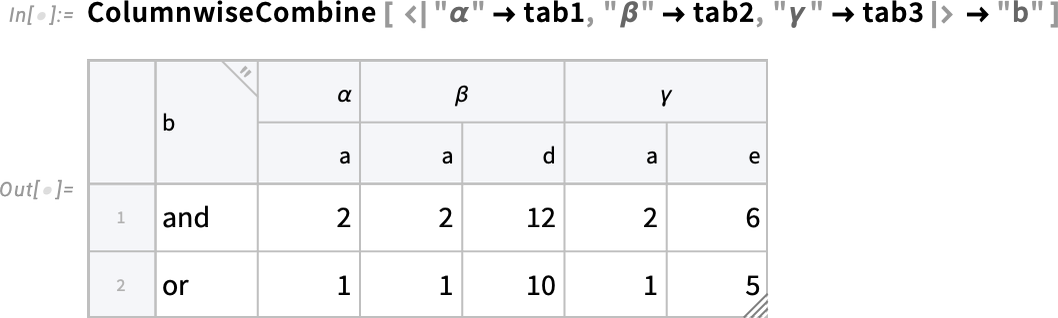
ColumnwiseCombine is in effect an n-ary generalization of JoinAcross (which in effect implements the “join” operation of relational algebra). And in Version 14.3 we also upgraded JoinAcross to handle more features of Tabular, for example being able to specify extended keys. And in both ColumnwiseCombine and JoinAcross we’ve set things up so that you can use an arbitrary function to determine whether rows should be combined.
Why would one want to use functions like ColumnwiseCombine and JoinAcross? A typical reason is that one has different Tabular objects that give intersecting sets of data that one wants to knit together for easier processing. So, for example, let’s say we have one Tabular that contains properties of isotopes, and another that contains properties of elements—and now we want to make a combined table of the isotopes, but now including extra columns brought in from the table of elements:
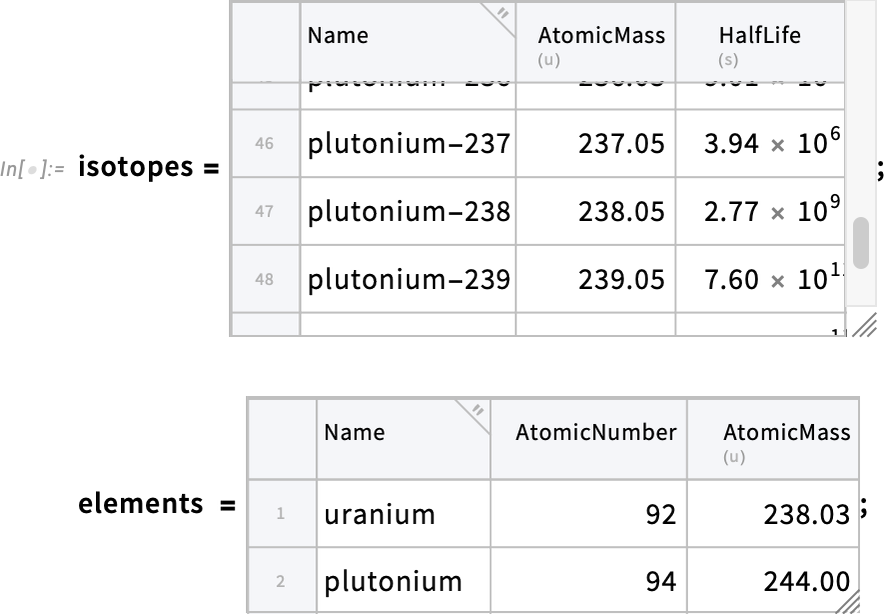
We can make the combined Tabular using JoinAcross. But in this particular case, as is often true with real-world data, the way we have to knit these tables of data together is a bit messy. The way we’ll do it is to use the third (“comparison function”) argument of JoinAcross, telling it to combine rows when the string corresponding to the entry for the "Name" column in the isotopes table has the same beginning as the string corresponding to the "Name" column in the elements table:
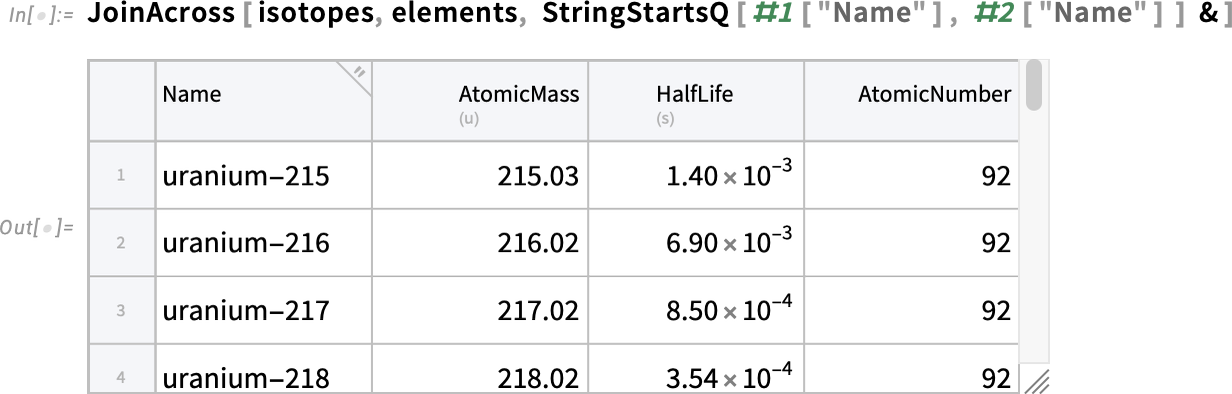
By default, we only get one column in the result with any given name. So, here, the "Name" column comes from the first Tabular in the JoinAcross (i.e. isotopes); the "AtomicNumber" column, for example, comes from the second (i.e. elements) Tabular. We can “disambiguate” the columns by their “source” by specifying a key in the JoinAcross:

So now we have a combined Tabular that has “knitted together” the data from both our original Tabular objects—a typical application of JoinAcross.
There’s a lot of powerful processing that can be done with Tabular. But Tabular is also a way to store—and present—data. And in Version 14.3 we’ve begun the process of providing capabilities to format Tabular objects and the data they contain. There are simple things. Like you can now use ImageSize to programmatically control the initial displayed size of a Tabular (you can always change the size interactively using the resize handle in the bottom right-hand corner):
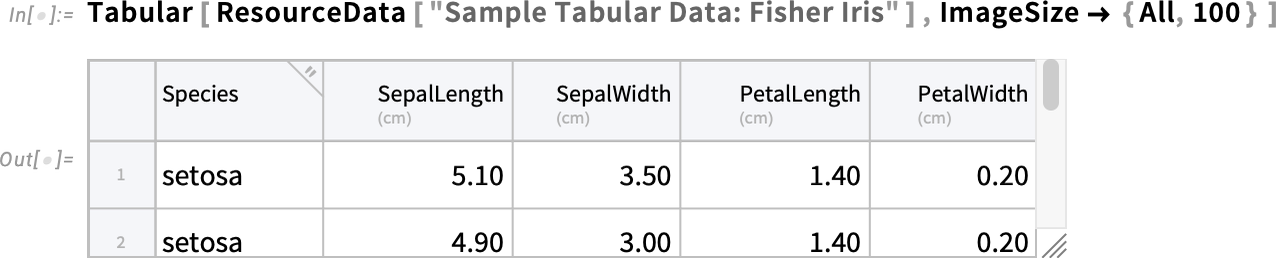
You can also use AppearanceElements to control what visual elements get included. Like here we’re asking for column headers, but no row labels or resize handle:
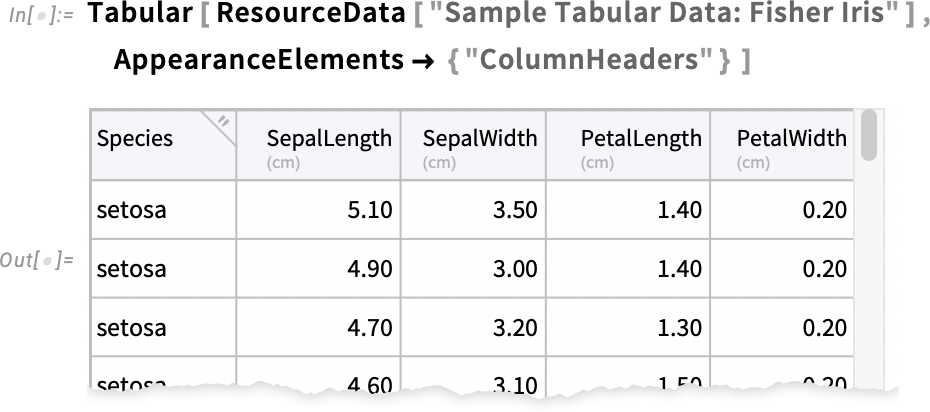
OK, but what about formatting for the data area? In Version 14.3 you can for example specify the background using the Background option. Here we’re asking for rows to alternately have no background or use light green (just like ancient line printer paper!):
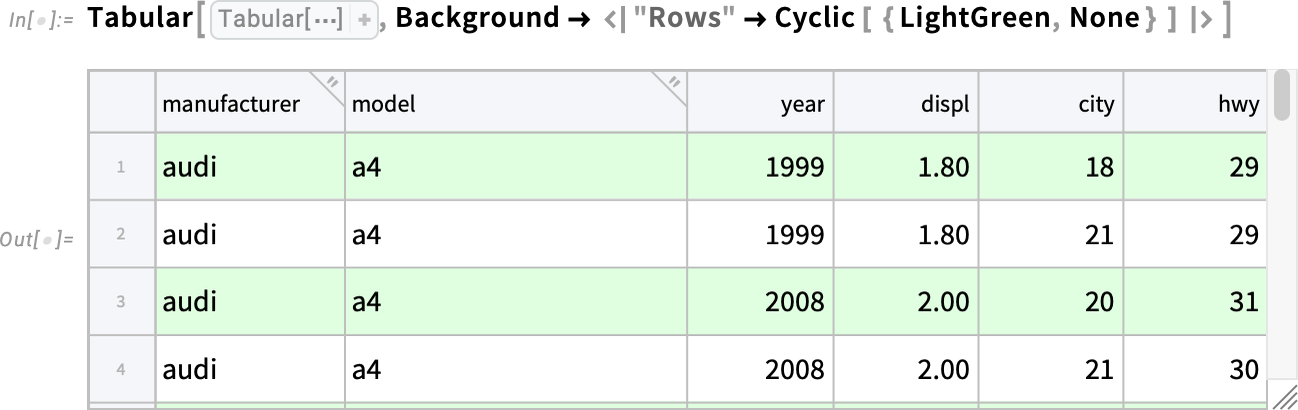
This puts a background on both rows and columns, with appropriate color mixing where they overlap:

This highlights just a single column by giving it a background color, specifying the column by name:
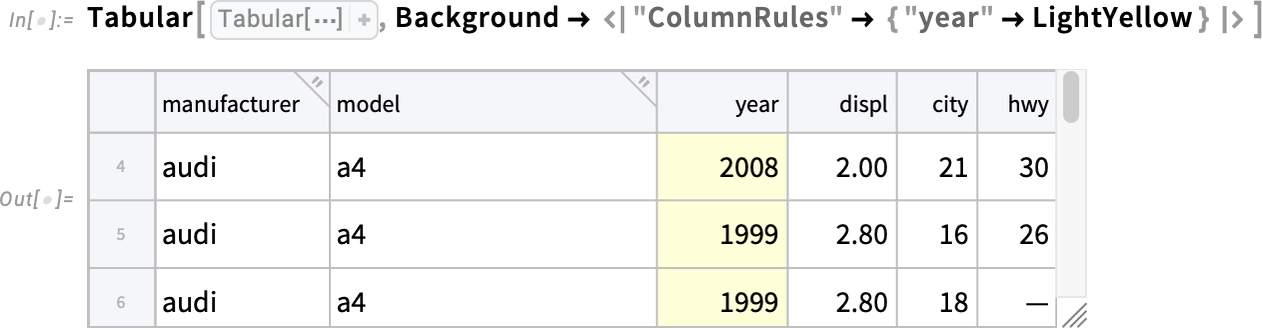
In addition to Background, Version 14.3 also supports specifying ItemStyle for the contents of Tabular. Here we’re saying to make the "year" column bold and red:
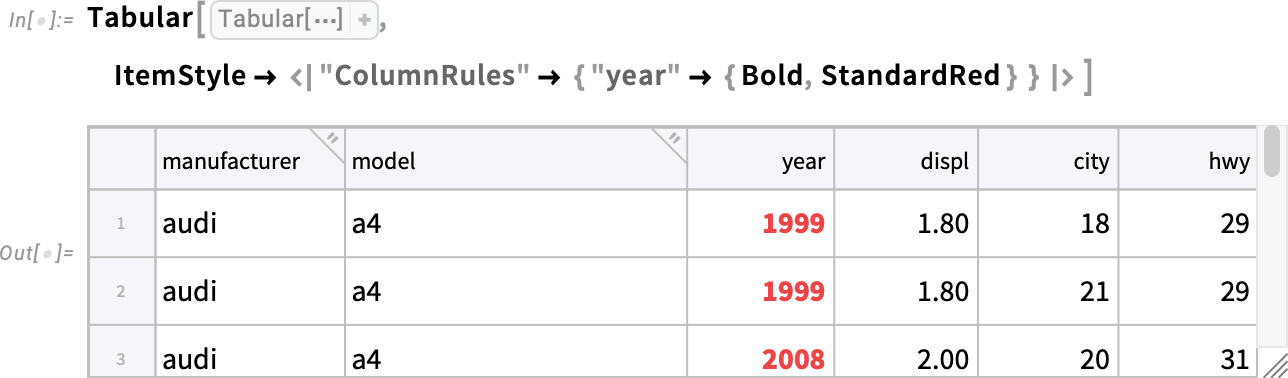
But what if you want the styling of elements in a Tabular to be determined not by their position, but by their value? Version 14.3 provides keys for that. For example, this puts a background color on every row for which the value of "hwy" is below 30:

We could do the same kind of thing, but having the color actually be computed from the value of "hwy" (or rather, from its value rescaled based on its overall “columnwise” min and max):

The last row shown here has no color—because the value in its "hwy" column is missing. And if you wanted, for example, to highlight all missing values you can just do this:

Which of those choices do you mean? Let’s say you’ve got a list of choices—for example a restaurant menu. And you give a textual description of what you want from those choices. The new function SemanticRanking will rank the choices according to what you say you want:

And because this is using modern language model methods, the choices could, for example, be given not only in English but in any language.
If you want, you can ask SemanticRanking to also give you things like relevance scores:

How does SemanticRanking relate to the SemanticSearch functionality that we introduced in Version 14.1? SemanticSearch actually by default uses SemanticRanking as a final ranking for the results it gives. But SemanticSearch is—as its name suggests—searching a potentially large amount of material, and returning the most relevant items from it. SemanticRanking, on the other hand, is taking a small “menu” of possibilities, and giving you a ranking of all of them based on relevance to what you specify.
SemanticRanking in effect exposes one of the elements of the SemanticSearch pipeline. In Version 14.3 we’re also exposing another element: an enhanced version of FeatureExtract for text, that is pre-trained, and does not require its own explicit examples:

Our new feature extractor for text also improves Classify, Predict, FeatureSpacePlot, etc. in the case of sentences or other pieces of text.
The typical flow of computation in the Wolfram Language is a sequence of function calls, with each function running and returning its result before another function is run. But Version 14.3 introduces—in the context of the Wolfram Language compiler—the possibility for a different kind of flow in which functions can be paused at any point, then resumed later. In effect what we’ve done is to implement a form of coroutines, that allows us to do incremental computation, and for example to support “generators” that can yield a sequence of results, always maintaining the state needed to produce more.
The basic idea is to set up an IncrementalFunction object that can be compiled. The IncrementalFunction object uses IncrementalYield to return “incremental” results—and can contain IncrementalReceive functions that allow it to receive more input while it is running.
Here’s a very simple example, set up to create an incremental function (represented as a DataStructure of type “IncrementalFunction”) that will keep successively generating powers of 2:

Now every time we ask for the "Next" element of this, the code in our incremental function runs until it reaches the IncrementalYield, at which point it yields the result specified:
In effect the compiled incremental function if is always internally “maintaining state” so that when we ask for the "Next" element it can just continue running from the state where it left off.
Here’s a slightly more complicated example: an incremental version of the Fibonacci recurrence:

Every time we ask for the "Next" element, we get the next result in the Fibonacci sequence:
The incremental function is set up to yield the value of a when you ask for the "Next" element, but internally it maintains the values of both a and b so that it is ready to “keep running” when you ask for another "Next" element.
In general, IncrementalFunction provides a new and often convenient way to organize code. You get to repeatedly run a piece of code and get results from it, but with the compiler automatically maintaining state, so you don’t explicitly have to take care of that, or include code to do it.
One common use case is in enumeration. Let’s say you have an algorithm for enumerating certain kinds of objects. The algorithm builds up an internal state that lets it keep generating new objects. With IncrementalFunction you can run the algorithm until it generates an object, then stop the algorithm, but automatically maintain the state to resume it again.
For example, here’s an incremental function for generating all possible pairs of elements from a specified list:

Let’s tell it to generate the pairs from a list of a million elements:

The complete collection of all these pairs wouldn’t fit in computer memory. But with our incremental function we can just successively request individual pairs, maintaining “where we’ve got to” inside the compiled incremental function:
Another thing one can do with IncrementalFunction is, for example, to incrementally consume some external stream of data, for example from a file or API.
IncrementalFunction is a new, core capability for the Wolfram Language that we’ll be using in future versions to build a whole array of new “incremental” functionality that lets one conveniently work (“incrementally”) with collections of objects that couldn’t be handled if one had to generate them all at once.
We’ve worked very hard (for decades!) to make things work as smoothly as possible when you’re working within the Wolfram Language. But what if you want to call external code? Well, it’s a jungle out there, with all kinds of issues of compatibility, dependencies, etc. But for years we’ve been steadily working to provide the best interface we can within Wolfram Language to external code. And in fact what we’ve managed to provide is now often a much smoother experience than with the native tools normally used with that external code.
Version 14.3 includes several advances in dealing with external code. First, for Python, we’ve dramatically sped up the provisioning of Python runtimes. Even the first time you use Python ever, it now takes just a few seconds to provision itself. In Version 14.2 we introduced a very streamlined way to specify dependencies. And now in Version 14.3 we’ve made provisioning of runtimes with particular dependencies very fast:

And, yes, a Python runtime with those dependencies will now be set up on your machine, so if you call it again, it can just run immediately, without any further provisioning.
A second major advance in Version 14.3 is the addition of a highly streamlined way of using R within Wolfram Language. Just specify R as the external language, and it’ll automatically be provisioned on your system, and then run a computation (yes, having "rnorm" as the name of the function that generates Gaussian random numbers offends my language design sensibilities, but…):
You can also use R directly in a notebook (type > to create an External Language cell):

One of the technical challenges is to set things up so that you can run R code with different dependencies within a single Wolfram Language session. We couldn’t do that before (and in some sense R is fundamentally not built to do it). But now in Version 14.3 we’ve set things up so that, in effect, there can be multiple R sessions running within your Wolfram Language session, each with their own dependencies, and own provisioning. (It’s really complicated to make this all work, and, yes, there might be some pathological cases where the world of R is just too tangled for it to be possible. But such cases should at least be very rare.)
Another thing we’ve added for R in Version 14.3 is support for ExternalFunction, so you can have code in R that you can set up to use just like any other function in Wolfram Language.
Notebooks are ordinarily intended to be scrolling documents. But—particularly if you’re making a presentation—you sometimes want them instead in more of a slide show form (“PowerPoint style”). We’d had various approaches before, but in Version 11.3—seven years ago—we introduced Presenter Tools as a streamlined way to make notebooks to use for presentations.
The principle of it is very convenient. You can either start from scratch, or you can convert an existing notebook. But what you get in the end is a slide show–like presentation, that you can for example step through with a presentation clicker. Of course, because it’s a notebook, you get all sorts of additional conveniences and features. Like you can have a Manipulate on your “slide”, or cell groups you can open and close. And you can also edit the “slide”, do evaluations, etc. It all works very nicely.
But there’s always been one big issue. You’re fundamentally trying to make what amount to slides—that will be shown full screen, perhaps projected, etc. But what aspect ratio will those slides have? And how does this relate to the content you have? For things like text, one can always reflow to fit into a different aspect ratio. But it’s trickier for graphics and images, because these already have their own aspect ratios. And particularly if these were somewhat exotic (say tall and narrow) one could end up with slides that required scrolling, or otherwise weren’t convenient or didn’t look good.
But now, in Version 14.3 we have a smooth solution for all this—that I know I, for one, am going to find very useful.
Choose File > New > Presenter Notebook… then press Create to create a new, blank presenter notebook:
In the toolbar, there’s now a new ![]() button that inserts a template for a full-slide image (or graphic):
button that inserts a template for a full-slide image (or graphic):
Insert an image—by copy/pasting, dragging (even from an external program) or whatever—with any aspect ratio:

Press ![]() and you’ll get a full-screen presentation—with everything sized right, the short-and-wide graphic spanning the width of my display, and the tall-and-narrow graphic spanning the height:
and you’ll get a full-screen presentation—with everything sized right, the short-and-wide graphic spanning the width of my display, and the tall-and-narrow graphic spanning the height:

When you insert a full-slide image, there’s always a “control bar” underneath:
![]()
The first pulldown

lets you decide whether the make the image fit in the window, or whether instead to make it fill out the window horizontally, perhaps clipping at the top and bottom.
Now remember that this template is for placing full-slide images. If you want there to be room, say for a caption, on the slide, you need to pick a size less than 100%.
By default, the background of the cells you get is determined by the original presenter notebook theme you chose. So in the example here, the default background will be white. And this means that if, for example, you’re projecting your images there’ll always be a “background white rectangle”. But if you want to just see your image projected—at its natural aspect ratio—with nothing visible around it, you can select Cell Background to instead be black.
It’s been 38 years since we invented notebooks… but in every new version we’re still continuing to polish and enhance how they work. Here’s an example. Nearly 30 years ago we introduced the idea that if you type -> it’ll get replaced by the more elegant ![]() . Four years ago (in Version 12.3) we tweaked this idea by having -> not actually be replaced by
. Four years ago (in Version 12.3) we tweaked this idea by having -> not actually be replaced by ![]() , but instead just render that one. But here’s a subtle question: if you arrow backwards through the
, but instead just render that one. But here’s a subtle question: if you arrow backwards through the ![]() does it show you the characters it’s made from? In previous versions it did, but now in Version 14.3 it doesn’t. It’s something we learned from experience: if you see something that looks like a single character (here
does it show you the characters it’s made from? In previous versions it did, but now in Version 14.3 it doesn’t. It’s something we learned from experience: if you see something that looks like a single character (here ![]() ) it’s strange and jarring for it to break apart if you arrow through it. So now it doesn’t. However, if you backspace (rather than arrowing), it will break apart, so you can edit the individual characters. Yes, it’s a subtle story, but getting it just right is one of those many, many things that makes the Wolfram Notebook experience so smooth.
) it’s strange and jarring for it to break apart if you arrow through it. So now it doesn’t. However, if you backspace (rather than arrowing), it will break apart, so you can edit the individual characters. Yes, it’s a subtle story, but getting it just right is one of those many, many things that makes the Wolfram Notebook experience so smooth.
Here’s another important little convenience that we’ve added in Version 14.3: single-character delimiter wrapping. Let’s say you typed this:
![]()
Most likely you actually wanted a list. And you can get it by adding { at the beginning, and } at the end. But now there’s a more streamlined thing to do. Just select everything
![]()
and now simply type {. The { … } will automatically get wrapped around the selection:
![]()
The same thing works with ( … ), [ … ], and “ … ”.
It may seem like a trivial thing. But if you’ve got lots of code on the screen, it’s very convenient to not have to go back and forth adding delimiters—but just be able to select some subexpression, then type a single character.
There’ve been a number of changes to icons, tooltips, etc. just to make things clearer. Something else is that (finally) there’s support for separate British and American English spelling dictionaries. By default, the choice of which one to use is made automatically from the setting for your operating system. But yes, “color” vs. “colour” and “center” vs. “centre” will now follow your preferences and get tagged appropriately. By the way, in case you’re wondering: we’ve been curating our own spelling dictionaries for years. And in fact, I routinely send in words to add, either because I find myself using them, or, yes, because I just invented them (“ruliad”, “emes”, etc.).
You want a file that’s plaintext but “formatted”. These days a common way to achieve that is to use Markdown. It’s a format both humans and AIs can easily read, and it can be “dressed up” to have visual formatting. Well, in Version 14.3 we’re making Markdown an easy-to-access format in Wolfram Notebooks, and in the Wolfram Language in general.
It should be said at the outset that Markdown isn’t even close to being as rich as our standard Notebook format. But many key elements of notebooks can still be captured by Markdown. (By the way, our .nb notebook files are, like Markdown, actually pure plaintext, but since they have to faithfully represent every aspect of notebook content, they’re inevitably not as spare and easy to read as Markdown files.)
OK, so let’s say you have a Notebook:

You can get a Markdown version just by using File > Save As > Markdown:

Here’s what this looks like in a Markdown viewer:
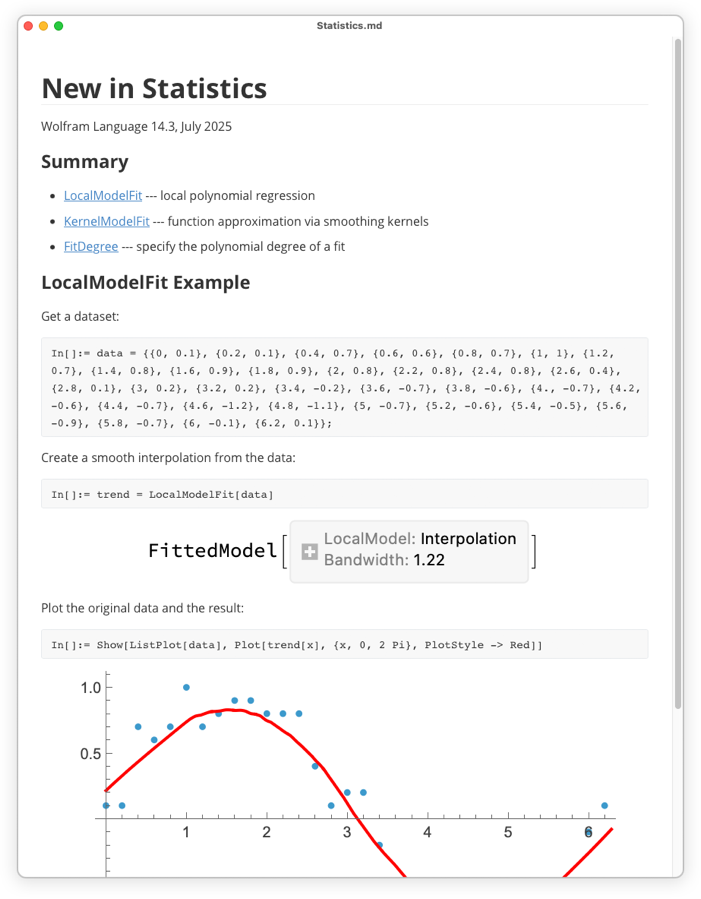
The main features of the notebook are there, but there are details missing (like cell backgrounds, real math typesetting, etc.), and the rendering is definitely not as beautiful as in our system nor as functional (for example, there are no closeable cell groups, no dynamic interactivity, etc.).
OK, so let’s say you have a Markdown file. In Version 14.3 you can now just use File > Open, choose Markdown Files as the file type, and open the Markdown file as a Notebook:
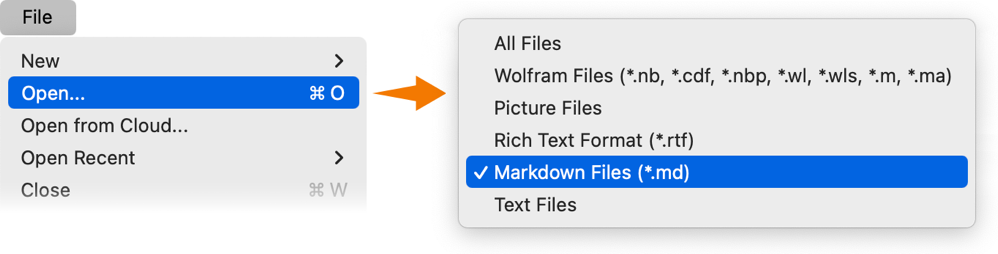
Round-tripping through Markdown loses some of the finer points of a Notebook, but the basic structure is there. And, yes, you can open Markdown files “from the wild” this way too, coming, for example, from notes apps, software documentation, raw LLM output, etc.
In addition to handling Markdown at a “whole file” level, you can also generate (and read) Markdown fragments. So, for example, you can take a table in a Notebook, then just do Copy As > Markdown to get a Markdown version:
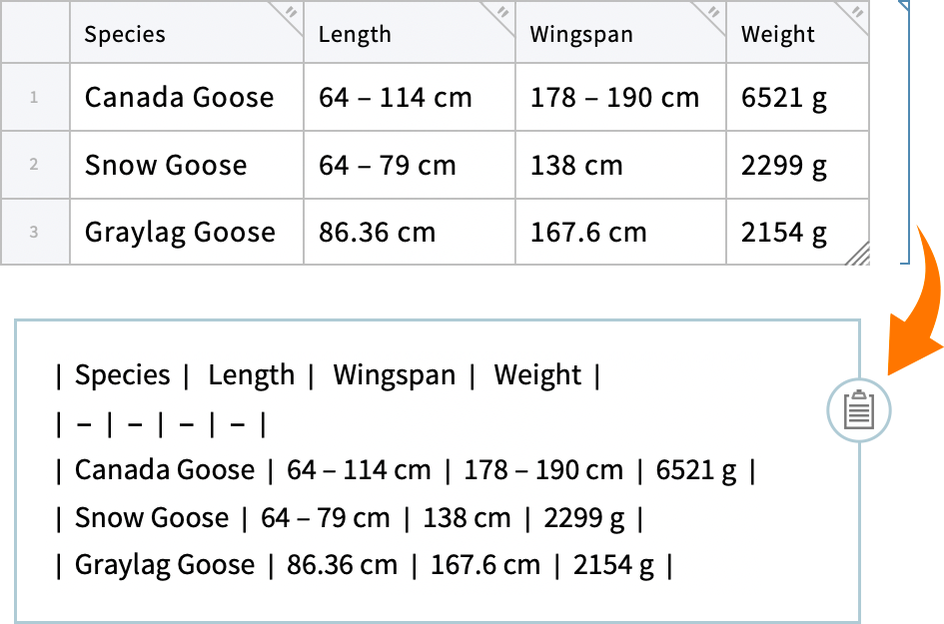
Needless to say, everything you can do interactively with Markdown, you can also do programmatically in the Wolfram Language. So, for example, you can use ExportString to export to Markdown:

Importing this gives by default plaintext:

But if you tell it to import as “formatted text”, it’ll package up the data in a tabular form:

Particularly when you’re communicating with LLMs, it’s often useful to have Markdown tables that are just “summaries” of longer, original tables. Here we’re asking for 3 rows of data:

And here we’re asking for 2 rows at the beginning, and 2 at the end:

There are lots of subtleties (and clever heuristics) associated with getting Markdown that’s as good—and round-trippable—as possible. If you export an image to Markdown


the actual Markdown will simply contain a pointer to a file that’s been created (in the img subdirectory) to store the image. This is particularly convenient if you’re using the Wolfram Cloud, where the images are embedded in the Markdown file as data URLs:

Ever since Version 13, there’s been a choice: download all 6.5 gigabytes of Wolfram Language documentation and use it locally, or just link to the web for documentation, without downloading anything. (By the way, if you want to download documentation, but haven’t, you can always do it with the Install Local Documentation item in the Help menu.)
In Version 14.3 there’s a new feature in web documentation. Assuming you have your browser window set fairly wide, there’s now a navigation sidebar on every function page:

Want to quickly look up how that option works? Just click it in the sidebar, and the page will jump down to where that option is described, opening the relevant cells:
Of course, in nearly 10,000 pages of rather diverse material, lots of complicated UX issues come up. Like with Plot, for example, the full list of options is very long, so by default it’s elided with ![]() :
:
Click the ![]() and all the options open up—with something like a cell bracket, that you can click to close it again:
and all the options open up—with something like a cell bracket, that you can click to close it again:

Version 14.3 is a strong release, full of new capabilities. And the things we’ve discussed so far aren’t even everything. There’s even more.
In video, for example, we’ve added VideoStabilize to take out jitter in videos. We’ve also enhanced VideoObjectTracking to let you specify particular points in a video to track. And if you effectively want to track every point, we’ve enhanced ImageDisplacements to work on videos.
In images, we now import .avif (AV1) files.
In speech synthesis, we’re now able to always do everything locally. In Version 14.2 we were using operating-system-based speech synthesis on Mac and Windows. Now we’ve got a collection of local neural net models that run consistently on any operating system—and whenever we can’t use operating-system-based speech synthesis, these are what we use.
Version 14.3 also adds yet more polish to our already very well developed system for handling dates. In particular, we’ve added new day types such as “NonHoliday” and “WeekendHoliday”, and we’ve provided an operator form of DayMatchQ—all in service of making it easy (and, by the way, very efficient) to more finely select specific types of dates, notably now in Tabular.
In a completely different area, Version 14.3 makes RandomTree much more efficient, and also allows trees with a specified list of node labels, here the alphabet:
Talking of efficiency, a small but useful enhancement to the world of DataStructure is that “BitVector” data structures now use multithreading, and the function Pick can operate directly on such data structures—including ones that are billions of bits long.
Also, in computation with GPUArray objects, we’ve further improved the performance of core arithmetic operations, as well as adding GPU support for functions like UnitStep and NumericalSort.
In the continuing story of partial differential equations and PDE modeling, Version 14.3 includes a new option for solving axisymmetric fluid flow problems—allowing one for example to compute this solution for flow through a pipe with a constriction:
In biochemistry, we’ve added connections to UniProt and the AlphaFold database. And in chemistry we’ve added various utility functions such as ChemicalFormulaQ and PatternReactionQ.
In the compiler we’ve added CurrentCompiledFunctionData to provide introspection on compiled functions, allowing you to determine, for example, what particular type the compiler assigned to the function you’re currently in:
Also in the compiler we’ve extended DownValuesFunction to let you “wrap for compilation” functions whose definitions involve constructs like Alternatives and Except. (This is a further precursor to letting you just directly compile raw downvalue assignments.)
In addition to all this, there are a large number of little tweaks and little pieces of polish that we’ve added in Version 14.3, along with over a thousand bug fixes: all things that make the experience of using Wolfram Language just that much smoother and richer.
Version 14.3 for desktop systems is ready for download now. It’s also now what you automatically get in the Wolfram Cloud. So… start using it today! And experience the fruits of the latest round of our intense research and development efforts…
2025-05-21 22:28:31

We humans have perhaps 100 billion neurons in our brains. But what if we had many more? Or what if the AIs we built effectively had many more? What kinds of things might then become possible? At 100 billion neurons, we know, for example, that compositional language of the kind we humans use is possible. At the 100 million or so neurons of a cat, it doesn’t seem to be. But what would become possible with 100 trillion neurons? And is it even something we could imagine understanding?
My purpose here is to start exploring such questions, informed by what we’ve seen in recent years in neural nets and LLMs, as well as by what we now know about the fundamental nature of computation, and about neuroscience and the operation of actual brains (like the one that’s writing this, imaged here):

One suggestive point is that as artificial neural nets have gotten bigger, they seem to have successively passed a sequence of thresholds in capability:

So what’s next? No doubt there’ll be things like humanoid robotic control that have close analogs in what we humans already do. But what if we go far beyond the ~1014 connections that our human brains have? What qualitatively new kinds of capabilities might there then be?
If this was about “computation in general” then there wouldn’t really be much to talk about. The Principle of Computational Equivalence implies that beyond some low threshold computational systems can generically produce behavior that corresponds to computation that’s as sophisticated as it can ever be. And indeed that’s the kind of thing we see both in lots of abstract settings, and in the natural world.
But the point here is that we’re not dealing with “computation in general”. We’re dealing with the kinds of computations that brains fundamentally do. And the essence of these seems to have to do with taking in large amounts of sensory data and then coming up with what amount to decisions about what to do next.
It’s not obvious that there’d be any reasonable way to do this. The world at large is full of computational irreducibility—where the only general way to work out what will happen in a system is just to run the underlying rules for that system step by step and see what comes out:

And, yes, there are plenty of questions and issues for which there’s essentially no choice but to do this irreducible computation—just as there are plenty of cases where LLMs need to call on our Wolfram Language computation system to get computations done. But brains, for the things most important to them, somehow seem to routinely manage to “jump ahead” without in effect simulating every detail. And what makes this possible is the fundamental fact that within any system that shows overall computational irreducibility there must inevitably be an infinite number of “pockets of computational reducibility”, in effect associated with “simplifying features” of the behavior of the system.
It’s these “pockets of reducibility” that brains exploit to be able to successfully “navigate” the world for their purposes in spite of its “background” of computational irreducibility. And in these terms things like the progress of science (and technology) can basically be thought of as the identification of progressively more pockets of computational reducibility. And we can then imagine that the capabilities of bigger brains could revolve around being able to “hold in mind” more of these pockets of computational reducibility.
We can think of brains as fundamentally serving to “compress” the complexity of the world, and extract from it just certain features—associated with pockets of reducibility—that we care about. And for us a key manifestation of this is the idea of concepts, and of language that uses them. At the level of raw sensory input we might see many detailed images of some category of thing—but language lets us describe them all just in terms of one particular symbolic concept (say “rock”).
In a rough first approximation, we can imagine that there’s a direct correspondence between concepts and words in our language. And it’s then notable that human languages all tend to have perhaps 30,000 common words (or word-like constructs). So is that scale the result of the size of our brains? And could bigger brains perhaps deal with many more words, say millions or more?
“What could all those words be about?” we might ask. After all, our everyday experience makes it seem like our current 30,000 words are quite sufficient to describe the world as it is. But in some sense this is circular: we’ve invented the words we have because they’re what we need to describe the aspects of the world we care about, and want to talk about. There will always be more features of, say, the natural world that we could talk about. It’s just that we haven’t chosen to engage with them. (For example, we could perfectly well invent words for all the detailed patterns of clouds in the sky, but those patterns are not something we currently feel the need to talk in detail about.)
But given our current set of words or concepts, is there “closure” to it? Can we successfully operate in a “self-consistent slice of concept space” or will we always find ourselves needing new concepts? We might think of new concepts as being associated with intellectual progress that we choose to pursue or not. But insofar as the “operation of the world” is computationally irreducible it’s basically inevitable that we’ll eventually be confronted with things that cannot be described by our current concepts.
So why is it that the number of concepts (or words) isn’t just always increasing? A fundamental reason is abstraction. Abstraction takes collections of potentially large numbers of specific things (“tiger”, “lion”, …) and allows them to be described “abstractly” in terms of a more general thing (say, “big cats”). And abstraction is useful if it’s possible to make collective statements about those general things (“all big cats have…”), in effect providing a consistent “higher-level” way of thinking about things.
If we imagine concepts as being associated with particular pockets of reducibility, the phenomenon of abstraction is then a reflection of the existence of networks of these pockets. And, yes, such networks can themselves show computational irreducibility, which can then have its own pockets of reducibility, etc.
So what about (artificial) neural nets? It’s routine to “look inside” these, and for example see the possible patterns of activation at a given layer based on a range of possible (“real-world”) inputs. We can then think of these patterns of activation as forming points in a “feature space”. And typically we’ll be able to see clusters of these points, which we can potentially identify as “emergent concepts” that we can view as having been “discovered” by the neural net (or rather, its training). Normally there won’t be existing words in human languages that correspond to most of these concepts. They represent pockets of reducibility, but not ones that we’ve identified, and that are captured by our typical 30,000 or so words. And, yes, even in today’s neural nets, there can easily be millions of “emergent concepts”.
But will these be useful abstractions or concepts, or merely “incidental examples of compression” not connected to anything else? The construction of neural nets implies that a pattern of “emergent concepts” at one layer will necessarily feed into the next layer. But the question is really whether the concept can somehow be useful “independently”—not just at this particular place in the neural net.
And indeed the most obvious everyday use for words and concepts—and language in general—is for communication: for “transferring thoughts” from one mind to another. Within a brain (or a neural net) there are all kinds of complicated patterns of activity, different in each brain (or each neural net). But a fundamental role that concepts, words and language play is to define a way to “package up” certain features of that activity in a form that can be robustly transported between minds, somehow inducing “comparable thoughts” in all of them.
The transfer from one mind to another can never be precise: in going from the pattern of activity in one brain (or neural net) to the pattern of activity in another, there’ll always be translation involved. But—at least up to a point—one can expect that the “more that’s said” the more faithful a translation can be.
But what if there’s a bigger brain, with more “emergent concepts” inside? Then to communicate about them at a certain level of precision we might need to use more words—if not a fundamentally richer form of language. And, yes, while dogs seem to understand isolated words (“sit”, “fetch”, …), we, with our larger brains, can deal with compositional language in which we can in effect construct an infinite range of meanings by combining words into phrases, sentences, etc.
At least as we currently imagine it, language defines a certain model of the world, based on some finite collection of primitives (words, concepts, etc.). The existence of computational irreducibility tells us that such a model can never be complete. Instead, the model has to “approximate things” based on the “network of pockets of reducibility” that the primitives in the language effectively define. And insofar as a bigger brain might in essence be able to make use of a larger network of pockets of reducibility, it can then potentially support a more precise model of the world.
And it could then be that if we look at such a brain and what it does, it will inevitably seem closer to the kind of “incomprehensible and irreducible computation” that’s characteristic of so many abstract systems, and systems in nature. But it could also be that in being a “brain-like construct” it’d necessarily tap into computational reducibility in such a way that—with the formalism and abstraction we’ve built—we’d still meaningfully be able to talk about what it can do.
At the outset we might have thought any attempt for us to “understand minds beyond ours” would be like asking a cat to understand algebra. But somehow the universality of the concepts of computation that we now know—with their ability to address the deepest foundations of physics and other fields—makes it seem more plausible we might now be in a position to meaningfully discuss minds beyond ours. Or at least to discuss the rather more concrete question of what brains like ours, but bigger than ours, might be able to do.
As we’ve mentioned, at least in a rough approximation, the role of brains is to turn large amounts of sensory input into small numbers of decisions about what to do. But how does this happen?
Human brains continually receive input from a few million “sensors”, mostly associated with photoreceptors in our eyes and touch receptors in our skin. This input is processed by a total of about 100 billion neurons, each responding in a few milliseconds, and mostly organized into a handful of layers. There are altogether perhaps 100 trillion connections between neurons, many quite long range. At any given moment, a few percent of neurons (i.e. perhaps a billion) are firing. But in the end, all that activity seems to feed into particular structures in the lower part of the brain that in effect “take a majority vote” a few times a second to determine what to do next—in particular with the few hundred “actuators” our bodies have.
This basic picture seems to be more or less the same in all higher animals. The total number of neurons scales roughly with the number of “input sensors” (or, in a first approximation, the surface area of the animal—i.e. volume2/3—which determines the number of touch sensors). The fraction of brain volume that consists of connections (“white matter”) as opposed to main parts of neurons (“gray matter”) increases as a power of the number of neurons. The largest brains—like ours—have a roughly nested pattern of folds that presumably reduce average connection lengths. Different parts of our brains have characteristic functions (e.g. motor control, handling input from our eyes, generation of language, etc.), although there seems to be enough universality that other parts can usually learn to take over if necessary. And in terms of overall performance, animals with smaller brains generally seem to react more quickly to stimuli.
So what was it that made brains originally arise in biological evolution? Perhaps it had to do with giving animals a way to decide where to go next as they moved around. (Plants, which don’t move around, don’t have brains.) And perhaps it’s because animals can’t “go in more than one direction at once” that brains seem to have the fundamental feature of generating a single stream of decisions. And, yes, this is probably why we have a single thread of “conscious experience”, rather than a whole collection of experiences associated with the activities of all our neurons. And no doubt it’s also what we leverage in the construction of language—and in communicating through a one-dimensional sequence of tokens.
It’s notable how similar our description of brains is to the basic operation of large language models: an LLM processes input from its “context window” by feeding it through large numbers of artificial neurons organized in layers—ultimately taking something like a majority vote to decide what token to generate next. There are differences, however, most notably that whereas brains routinely intersperse learning and thinking, current LLMs separate training from operation, in effect “learning first” and “thinking later”.
But almost certainly the core capabilities of both brains and neural nets don’t depend much on the details of their biological or architectural structure. It matters that there are many inputs and few outputs. It matters that there’s irreducible computation inside. It matters that the systems are trained on the world as it is. And, finally, it matters how “big” they are, in effect relative to the “number of relevant features of the world”.
In artificial neural nets, and presumably also in brains, memory is encoded in the
strengths (or “weights”) of connections between neurons. And at least in neural nets it seems that the number of tokens (of textual data) that can reasonably be “remembered” is a few times the number of weights. (With current methods, the number of computational operations of training needed to achieve this is roughly the product of the total number of weights and the total number of tokens.) If there are too few weights, what happens is that the “memory” gets fuzzy, with details of the fuzziness reflecting details of the structure of the network.
But what’s crucial—for both neural nets and brains—is not so much to remember specifics of training data, but rather to just “do something reasonable” for a wide range of inputs, regardless of whether they’re in the training data. Or, in other words, to generalize appropriately from training data.
But what is “appropriate generalization”? As a practical matter, it tends to be “generalization that aligns with what we humans would do”. And it’s then a remarkable fact that artificial neural nets with fairly simple architectures can successfully do generalizations in a way that’s roughly aligned with human brains. So why does this work? Presumably it’s because there are universal features of “brain-like systems” that are close enough between human brains and neural nets. And once again it’s important to emphasize that what’s happening in both cases seems distinctly weaker than “general computation”.
A feature of “general computation” is that it can potentially involve unbounded amounts of time and storage space. But both brains and typical neural nets have just a fixed number of neurons. And although both brains and LLMs in effect have an “outer loop” that can “recycle” output to input, it’s limited.
And at least when it comes to brains, a key feature associated with this is the limit on “working memory”, i.e. memory that can readily be both read and written “in the course of a computation”. Bigger and more developed brains typically seem to support larger amounts of working memory. Adult humans can remember perhaps 5 or 7 “chunks” of data in working memory; for young children, and other animals, it’s less. Size of working memory (as we’ll discuss later) seems to be important in things like language capabilities. And the fact that it’s limited is no doubt one reason we can’t generally “run code in our brains”.
As we try to reflect on what our brains do, we’re most aware of our stream of conscious thought. But that represents just a tiny fraction of all our neural activity. Most of the activity is much less like “thought” and much more like typical processes in nature, with lots of elements seemingly “doing their own thing”. We might think of this as an “ocean of unconscious neural activity”, from which a “thread of consensus thought” is derived. Usually—much like in an artificial neural net—it’s difficult to find much regularity in that “unconscious activity”. Though when one trains oneself enough to get to the point of being able to “do something without thinking about it”, that presumably happens by organizing some part of that activity.
There’s always a question of what kinds of things we can learn. We can’t overcome computational irreducibility. But how broadly can we handle what’s computationally reducible? Artificial neural nets show a certain genericity in their operation: although some specific architectures are more efficient than others, it doesn’t seem to matter much whether the input they’re fed is images or text or numbers, or whatever. And for our brains it’s probably the same—though what we’ve normally experienced, and learned from, are the specific kinds of input that come from our eyes, ears, etc. And from these, we’ve ended up recognizing certain types of regularities—that we’ve then used to guide our actions, set up our environment, etc.
And, yes, this plugs into certain pockets of computational reducibility in the world. But there’s always further one could go. And how that might work with brains bigger than ours is at the core of what we’re trying to discuss here.
At some level we can view our brains as serving to take the complexity of the world and extract from it a compressed representation that our finite minds can handle. But what is the structure of that representation? A central aspect of it is that it ignores many details of the original input (like particular configurations of pixels). Or, in other words, it effectively equivalences many different inputs together.
But how then do we describe that equivalence class? Implementationally, say in a neural net, the equivalence class might correspond to an attractor to which many different initial conditions all evolve. In terms of the detailed pattern of activity in the neural net the attractor will typically be very hard to describe. But on a larger scale we can potentially just think of it as some kind of robust construct that represents a class of things—or what in terms of our process of thought we might describe as a “concept”.
At the lowest level there’s all sorts of complicated neural activity in our brains—most of it mired in computational irreducibility. But the “thin thread of conscious experience” that we extract from this we can for many purposes treat as being made up of higher-level “units of thought”, or essentially “discrete concepts”.
And, yes, it’s certainly our typical human experience that robust constructs—and particularly ones from which other constructs can be built—will be discrete. In principle one can imagine that there could be things like “robust continuous spaces of concepts” (“cat and dog and everything in between”). But we don’t have anything like the computational paradigm that shows us a consistent universal way that such things could fit together (there’s no robust analog of computation theory for real numbers, for example). And somehow the success of the computational paradigm—potentially all the way down to the foundations of the physical universe—doesn’t seem to leave much room for anything else.
So, OK, let’s imagine that we can represent our thread of conscious experience in terms of concepts. Well, that’s close to saying that we’re using language. We’re “packaging up” the details of our neural activity into “robust elements” which we can think of as concepts—and which are represented in language essentially by words. And not only does this “packaging” into language give a robust way for different brains to communicate; it also gives a single brain a robust way to “remember” and “redeploy” thoughts.
Within one brain one could imagine that one might be able to remember and “think” directly in terms of detailed low-level neural patterns. But no doubt the “neural environment” inside a brain is continually changing (not least because of its stream of sensory input). And so the only way to successfully “preserve a thought” across time is presumably to “package it up” in terms of robust elements, or essentially in terms of language. In other words, if we’re going to be able to consistently “think a particular thought” we probably have to formulate it in terms of something robust—like concepts.
But, OK, individual concepts are one thing. But language—or at least human language—is based on putting together concepts in structured ways. One might take a noun (“cat”) and qualify it with an adjective (“black”) to form a phrase that’s in effect a finer-grained version of the concept represented by the noun. And in a rough approximation one can think of language as formed from trees of nested phrases like this. And insofar as the phrases are independent in their structure (i.e. “context free”), we can parse such language by recursively understanding each phrase in turn—with the constraint that we can’t do it if the nesting goes too deep for us to hold the necessary stack of intermediate steps in our working memory.
An important feature of ordinary human language is that it’s ultimately presented in a sequential way. Even though it may consist of a nested tree of phrases, the words that are the leaves of that tree are spoken or written in a one-dimensional sequence. And, yes, the fact that this is how it works is surely closely connected to the fact that our brains construct a single thread of conscious experience.
In the actuality of the few thousand human languages currently in use, there is considerable superficial diversity, but also considerable fundamental commonality. For example, the same parts of speech (noun, verb, etc.) typically show up, as do concepts like “subject” and “object”. But the details of how words are put together, and how things are indicated, can be fairly different. Sometimes nouns have case endings; sometimes there are separate prepositions. Sometimes verb tenses are indicated by annotating the verb; sometimes with extra words. And sometimes, for example, what would usually be whole phrases can be smooshed together into single words.
It’s not clear to what extent commonalities between languages are the result of shared history, and to what extent they’re consequences either of the particulars of our human sensory experience of the world, or the particular construction of our brains. It’s not too hard to get something like concepts to emerge in experiments on training neural nets to pass data through a “bottleneck” that simulates a “mind-to-mind communication channel”. But how compositionality or grammatical structure might emerge is not clear.
OK, but so what might change if we had bigger brains? If neural nets are a guide, one obvious thing is that we should be able to deal directly with a larger number of “distinct concepts”, or words. So what consequences would this have? Presumably one’s language would get “grammatically shallower”, in the sense that what would otherwise have had to be said with nested phrases could now be said with individual words. And presumably this would tend to lead to “faster communication”, requiring fewer words. But it would likely also lead to more rigid communication, with less ability to tweak shades of meaning, say by changing just a few words in a phrase. (And it would presumably also require longer training, to learn what all the words mean.)
In a sense we have a preview of what it’s like to have more words whenever we deal with specialized versions of existing language, aimed say at particular technical fields. There are additional words of “jargon” available, that make certain things “faster to say” (but require longer to learn). And with that jargon comes a certain rigidity, in saying easily only what the jargon says, and not something slightly different.
So how else could language be different with a bigger brain? With larger working memory, one could presumably have more deeply nested phrases. But what about more sophisticated grammatical structures, say ones that aren’t “context free”, in the sense that different nested phrases can’t be parsed separately? My guess is that this quickly devolves into requiring arbitrary computation—and runs into computational irreducibility. In principle it’s perfectly possible to have any program as the “message” one communicates. But if one has to run the program to “determine its meaning”, that’s in general going to involve computational irreducibility.
And the point is that with our assumptions about what “brain-like systems” do, that’s something that’s out of scope. Yes, one can construct a system (even with neurons) that can do it. But not with the “single thread of decisions from sensory input” workflow that seems characteristic of brains. (There are finer gradations one could consider—like languages that are context sensitive but don’t require general computation. But the Principle of Computational Equivalence strongly suggests that the separation between nested context-free systems and ones associated with arbitrary computation is very thin, and there doesn’t seem to be any particular reason to expect that the capabilities of a bigger brain would land right there.)
Said another way: the Principle of Computational Equivalence says it’s easy to have a system that can deal with arbitrary computation. It’s just that such a system is not “brain like” in its behavior; it’s more like a typical system we see in nature.
OK, but what other “additional features” can one imagine, for even roughly “brain-like” systems? One possibility is to go beyond the idea of a single thread of experience, and to consider a multiway system in which threads of experience can branch and merge. And, yes, this is what we imagine happens at a low level in the physical universe, particularly in connection with quantum mechanics. And indeed it’s perfectly possible to imagine, for example, a “quantum-like” LLM system in which one generates a graph of different textual sequences. But just “scaling up the number of neurons” in a brain, without changing the overall architecture, won’t get to this. We have to have a different, multiway architecture. Where we have a “graph of consciousness” rather than a “stream of consciousness”, and where, in effect, we’re “thinking a graph of thoughts”, notably with thoughts themselves being able to branch and merge.
In our practical use of language, it’s most often communicated in spoken or written form—effectively as a one-dimensional sequence of tokens. But in math, for example, it’s common to have a certain amount of 2D structure, and in general there are also all sorts of specialized (usually technical) diagrammatic representations in use, often based on using graphs and networks—as we’ll discuss in more detail below.
But what about general pictures? Normally it’s difficult for us to produce these. But in generative AI systems it’s basically easy. So could we then imagine directly “communicating mental images” from one mind to another? Maybe as a practical matter some neural implant in our brain could aggregate neural signals from which a displayed image could be generated. But is there in fact something coherent that could be extracted from our brains in this way? Perhaps that can only happen after “consensus is formed”, and we’ve reduced things to a much thinner “thread of experience”. Or, in other words, perhaps the only robust way for us to “think about images” is in effect to reduce them to discrete concepts and language-like representations.
But perhaps if we “had the hardware” to display images directly from our minds it’d be a different story. And it’s sobering to imagine that perhaps the reason cats and dogs don’t appear to have compositional language is just that they don’t “have the hardware” to talk like we do (and it’s too laborious for them to “type with their paws”, etc.). And, by analogy, that if we “had the hardware” for displaying images, we’d discover we could also “think very differently”.
Of course, in some small ways we do have the ability to “directly communicate with images”, for example in our use of gestures and body language. Right now, these seem like largely ancillary forms of communication. But, yes, it’s conceivable that with bigger brains, they could be more.
And when it comes to other animals the story can be different. Cuttlefish are notable for dynamically producing elaborate patterns on their skin—giving them in a sense the hardware to “communicate in pictures”. But so far as one can tell, they produce just a small number of distinct patterns—and certainly nothing like a “pictorial generalization of compositional language”. (In principle one could imagine that “generalized cuttlefish” could do things like “dynamically run cellular automata on their skin”, just like all sorts of animals “statically” do in the process of growth or development. But to decode such patterns—and thereby in a sense enable “communicating in programs”—would typically require irreducible amounts of computation that are beyond the capabilities of any standard brain-like system.)
We humans have raw inputs coming into our brains from a few million sensors distributed across our usual senses of touch, sight, hearing, taste and smell (together with balance, temperature, hunger, etc.). In most cases the detailed sensor inputs are not independent; in a typical visual scene, for example, neighboring pixels are highly correlated. And it doesn’t seem to take many layers of neurons in our brains to distill our typical sensory experience from pure pieces of “raw data” to what we might view as “more independent features”.
Of course there’ll usually be much more in the raw data than just those features. But the “features” typically correspond to aspects of the data that we’ve “learned are useful to us”—normally connected to pockets of computational reducibility that exist in the environment in which we operate. Are the features we pick out all we’ll ever need? In the end, we typically want to derive a small stream of decisions or actions from all the data that comes in. But how many “intermediate features” do we need to get “good” decisions or actions?
That really depends on two things. First, what our decisions and actions are like. And second, what our raw data is like. Early in the history of our species, everything was just about “indigenous human experience”: what the natural world is like, and what we can do with our bodies. But as soon as we were dealing with technology, that changed. And in today’s world we’re constantly exposed, for example, to visual input that comes not from the natural world, but, say, from digital displays.
And, yes, we often try to arrange our “user experience” to align with what’s familiar from the natural world (say by having objects that stay unchanged when they’re moved across the screen). But it doesn’t have to be that way. And indeed it’s easy—even with simple programs—to generate for example visual images very different from what we’re used to. And in many such cases, it’s very hard for us to “tell what’s going on” in the image. Sometimes it’ll just “look too complicated”. Sometimes it’ll seem like it has pieces we should recognize, but we don’t:

When it’s “just too complicated”, that’s often a reflection of computational irreducibility. But when there are pieces we might “think we should recognize”, that can be a reflection of pockets of reducibility we’re just not familiar with. If we imagine a space of possible images—as we can readily produce with generative AI—there will be some that correspond to concepts (and words) we’re familiar with. But the vast majority will effectively lie in “interconcept space”: places where we could have concepts, but don’t, at least yet:

So what could bigger brains do with all this? Potentially they could handle more features, and more concepts. Full computational irreducibility will always in effect ultimately overpower them. But when it comes to handling pockets of reducibility, they’ll presumably be able to deal with more of them. So in the end, it’s very much as one might expect: a bigger brain should be able to track more things going on, “see more details”, etc.
Brains of our size seem like they are in effect sufficient for “indigenous human experience”. But with technology in the picture, it’s perfectly possible to “overload” them. (Needless to say, technology—in the form of filtering, data analysis, etc.—can also reduce that overload, in effect taking raw input and bringing our actual experience of it closer to something “indigenous”.)
It’s worth pointing out that while two brains of a given size might be able to “deal with the same number of features or concepts”, those features or concepts might be different. One brain might have learned to talk about the world in terms of one set of primitives (such as certain basic colors); another in terms of a different set of primitives. But if both brains are sampling “indigenous human experience” in similar environments one can expect that it should be possible to translate between these descriptions—just as it is generally possible to translate between things said in different human languages.
But what if the brains are effectively sampling “different slices of reality”? What if one’s using technology to convert different physical phenomena to forms (like images) that we can “indigenously” handle? Perhaps we’re sensing different electromagnetic frequencies; perhaps we’re sensing molecular or chemical properties; perhaps we’re sensing something like fluid motion. The kinds of features that will be “useful” may be quite different in these different modalities. Indeed, even something as seemingly basic as the notion of an “object” may not be so relevant if our sensory experience is effectively of continuous fluid motion.
But in the end, what’s “useful” will depend on what we can do. And once again, it depends on whether we’re dealing with “pure humans” (who can’t, for example, move like octopuses) or with humans “augmented by technology”. And here we start to see an issue that relates to the basic capabilities of our brains.
As “pure humans”, we have certain “actuators” (basically in the form of muscles) that we can “indigenously” operate. But with technology it’s perfectly possible for us to use quite different actuators in quite different configurations. And as a practical matter, with brains like ours, we may not be able to make them work.
For example, while humans can control helicopters, they never managed to control quadcopters—at least not until digital flight controllers could do most of the work. In a sense there were just too many degrees of freedom for brains like ours to deal with. Should bigger brains be able to do more? One would think so. And indeed one could imagine testing this with artificial neural nets. In millipedes, for example, their actual brains seem to support only a couple of patterns of motion of their legs (roughly, same phase vs. opposite phase). But one could imagine that with a bigger brain, all sorts of other patterns would become possible.
Ultimately, there are two issues at stake here. The first is having a brain be able to “independently address” enough actuators, or in effect enough degrees of freedom. The second is having a brain be able to control those degrees of freedom. And for example with mechanical degrees of freedom there are again essentially issues of computational irreducibility. Looking at the space of possible configurations—say of millipede legs—does one effectively just have to trace the path to find out if, and how, one can get from one configuration to another? Or are there instead pockets of reducibility, associated with regularities in the space of configurations, that let one “jump ahead” and figure this out without tracing all the steps? It’s those pockets of reducibility that brains can potentially make use of.
When it comes to our everyday “indigenous” experience of the world, we are used to certain kinds of computational reducibility, associated for example with familiar natural laws, say about motion of objects. But what if we were dealing with different experiences, associated with different senses?
For example, imagine (as with dogs) that our sense of smell was better developed than our sense of sight—as reflected by more nerves coming into our brains from our noses than our eyes. Our description of the world would then be quite different, based for example not on geometry revealed by the line-of-sight arrival of light, but instead by the delivery of odors through fluid motion and diffusion—not to mention the probably-several-hundred-dimensional space of odors, compared to the red, green, blue space of colors. Once again there would be features that could be identified, and “concepts” that could be defined. But those might only be useful in an environment “built for smell” rather than one “built for sight”.
And in the end, how many concepts would be useful? I don’t think we have any way to know. But it certainly seems as if one can be a successful “smell-based animal” with a smaller brain (presumably supporting fewer concepts) than one needs as a successful “sight-based animal”.
One feature of “natural senses” is that they tend to be spatially localized: an animal basically senses things only where it is. (We’ll discuss the case of social organisms later.) But what if we had access to a distributed array of sensors—say associated with IoT devices? The “effective laws of nature” that one could perceive would then be different. Maybe there would be regularities that could be captured by a small number of concepts, but it seems more likely that the story would be more complicated, and that in effect one would “need a bigger brain” to be able to keep track of what’s going on, and make use of whatever pockets of reducibility might exist.
There are somewhat similar issues if one imagines changing the timescales for sensory input. Our perception of space, for example, depends on the fact that light travels fast enough that in the milliseconds it takes our brain to register the input, we’ve already received light from everything that’s around us. But if our brains operated a million times faster (as digital electronics does) we’d instead be registering individual photons. And while our brains might aggregate these to something like what we ordinarily perceive, there may be all sorts of other (e.g. quantum optics) effects that would be more obvious.
The more abstractly we try to think, the harder it seems to get. But would it get easier if we had bigger brains? And might there perhaps be fundamentally higher levels of abstraction that we could reach—but only if we had bigger brains.
As a way to approach such questions, let’s begin by talking a bit about the history of the phenomenon of abstraction. We might already say that basic perception involves some abstraction, capturing as it does a filtered version of the world as it actually is. But perhaps we reach a different level when we start to ask “what if?” questions, and to imagine how things in the world could be different than they are.
But somehow when it comes to us humans, it seems as if the greatest early leap in abstraction was the invention of language, and the explicit delineation of concepts that could be quite far from our direct experience. The earliest written records tend to be rather matter of fact, mostly recording as they do events and transactions. But already there are plenty of signs of abstraction. Numbers independent of what they count. Things that should happen in the future. The concept of money.
There seems to be a certain pattern to the development of abstraction. One notices that some category of things one sees many times can be considered similar, then one “packages these up” into a concept, often described by a word. And in many cases, there’s a certain kind of self amplification: once one has a word for something (as a modern example, say “blog”), it becomes easier for us to think about the thing, and we tend to see it or make it more often in the world around us. But what really makes abstraction take off is when we start building a whole tower of it, with one abstract concept recursively being based on others.
Historically this began quite slowly. And perhaps it was seen first in theology. There were glimmerings of it in things like early (syllogistic) logic, in which one started to be able to talk about the form of arguments, independent of their particulars. And then there was mathematics, where computations could be done just in terms of numbers, independent of where those numbers came from. And, yes, while there were tables of “raw computational results”, numbers were usually discussed in terms of what they were numbers of. And indeed when it came to things like measures of weight, it took until surprisingly modern times for there to be an absolute, abstract notion of weight, independent of whether it was a weight of figs or of wool.
The development of algebra in the early modern period can be considered an important step forward in abstraction. Now there were formulas that could be manipulated abstractly, without even knowing what particular numbers x stood for. But it would probably be fair to say that there was a major acceleration in abstraction in the 19th century—with the development of formal systems that could be discussed in “purely symbolic form” independent of what they might (or might not) “actually represent”.
And it was from this tradition that modern notions of computation emerged (and indeed particularly ones associated with symbolic computation that I personally have extensively used). But the most obvious area in which towers of abstraction have been built is mathematics. One might start with numbers (that could count things). But soon one’s on to variables, functions, spaces of functions, category theory—and a zillion other constructs that abstractly build on each other.
The great value of abstraction is that it allows one to think about large classes of things all at once, instead of each separately. But how do those abstract concepts fit together? The issue is that often it’s in a way that’s very remote from anything about which we have direct experience from our raw perception of the world. Yes, we can define concepts about transfinite numbers or higher categories. But they don’t immediately relate to anything we’re familiar with from our everyday experience.
As a practical matter one can often get a sense of how high something is on the tower of abstraction by seeing how much one has to explain to build up to it from “raw experiential concepts”. Just sometimes it turns out that actually, once one hears about a certain seemingly “highly abstract” concept, one can actually explain it surprisingly simply, without going through the whole historical chain that led to it. (A notable example of this is the concept of universal computation—which arose remarkably late in human intellectual history, but is now quite easy to explain, albeit particularly given its actual widespread embodiment in technology.) But the more common case is that there’s no choice but to explain a whole tower of concepts.
At least in my experience, however, when one actually thinks about “highly abstract” things, one does it by making analogies to more familiar, more concrete things. The analogies may not be perfect, but they provide scaffolding which allows our brains to take what would otherwise be quite inaccessible steps.
At some level any abstraction is a reflection of a pocket of computational reducibility. Because if a useful abstraction can be defined, what it means is that it’s possible to say something in a “summarized” or reduced way, in effect “jumping ahead”, without going through all the computational steps or engaging with all the details. And one can then think of towers of abstraction as being like networks of pockets of computational reducibility. But, yes, it can be hard to navigate these.
Underneath, there’s lots of computational irreducibility. And if one is prepared to “go through all the steps” one can often “get to an answer” without all the “conceptual difficulty” of complex abstractions. But while computers can often readily “go through all the steps”, brains can’t. And that’s in a sense why we have to use abstraction. But inevitably, even if we’re using abstraction, and the pockets of computational reducibility associated with it, there’ll be shadows of the computational irreducibility underneath. And in particular, if we try to “explore everything”, our network of pockets of reducibility will inevitably “get complicated”, and ultimately also be mired in computational irreducibility, albeit with “higher-level” constructs than in the computational irreducibility underneath.
No finite brain will ever be able to “go all the way”, but it starts to seem likely that a bigger brain will be able to “reach further” in the network of abstraction. But what will it find there? How does the character of abstraction change when we take it further? We’ll be able to discuss this a bit more concretely when we talk about computational language below. But perhaps the main thing to say now is that—at least in my experience—most higher abstractions don’t feel as if they’re “structurally different” once one understands them. In other words, most of the time, it seems as if the same patterns of thought and reasoning that one’s applied in many other places can be applied there too, just to different kinds of constructs.
Sometimes, though, there seem to be exceptions. Shocks to intuition that seem to separate what one’s now thinking about from anything one’s thought before. And, for example, for me this happened when I started looking broadly at the computational universe. I had always assumed that simple rules would lead to simple behavior. But many years ago I discovered that in the computational universe this isn’t true (hence computational irreducibility). And this led to a whole different paradigm for thinking about things.
It feels a bit like in metamathematics. Where one can imagine one type of abstraction associated with different constructs out of which to form theorems. But where somehow there’s another level associated with different ways to build new theorems, or indeed whole spaces of theorems. Or to build proofs from proofs, or proofs from proofs of proofs, etc. But the remarkable thing is that there seems to be an ultimate construct that encompasses it all: the ruliad.
We can describe the ruliad as the entangled limit of all possible computations. But we can also describe it as the limit of all possible abstractions. And it seems to lie underneath all physical reality, as well as all possible mathematics, etc. But, we might ask, how do brains relate to it?
Inevitably, it’s full of computational irreducibility. And looked at as a whole, brains can’t get far with it. But the key idea is to think about how brains as they are—with all their various features and limitations—will “parse” it. And what I’ve argued is that what “brains as they are” will perceive about the ruliad are the core laws of physics (and mathematics) as we know them. In other words, it’s because brains are the way they are that we perceive the laws of physics that we perceive.
Would it be different for bigger brains? Not if they’re the “same kind of brains”. Because what seems to matter for the core laws of physics are really just two properties of observers. First, that they’re computationally bounded. And second, that they believe they are persistent in time, and have a single thread of experience through time. And both of these seem to be core features of what makes brains “brain-like”, rather than just arbitrary computational systems.
It’s a remarkable thing that just these features are sufficient to make core laws of physics inevitable. But if we want to understand more about the physics we’ve constructed—and the laws we’ve deduced—we probably have to understand more about what we’re like as observers. And indeed, as I’ve argued elsewhere, even our physical scale (much bigger than molecules, much smaller than the whole universe) is for example important in giving us the particular experience (and laws) of physics that we have.
Would this be different with bigger brains? Perhaps a little. But anything that something brain-like can do pales in comparison to the computational irreducibility that exists in the ruliad and in the natural world. Nevertheless, with every new pocket of computational reducibility that’s reached we get some new abstraction about the world, or in effect, some new law about how the world works.
And as a practical matter, each such abstraction can allow us to build a whole collection of new ways of thinking about the world, and making things in the world. It’s challenging to trace this arc. Because in a sense it’ll all be about “things we never thought to think about before”. Goals we might define for ourselves that are built on a tower of abstraction, far away from what we might think of as “indigenous human goals”.
It’s important to realize that there won’t just be one tower of abstraction that can be built. There’ll inevitably be an infinite network of pockets of computational reducibility, with each path leading to a different specific tower of abstraction. And indeed the abstractions we have pursued reflect the particular arc of human intellectual history. Bigger brains—or AIs—have many possible directions they can go, each one defining a different path of history.
One question to ask is to what extent reaching higher levels of abstraction is a matter of education, and to what extent it requires additional intrinsic capabilities of a brain. It is, I suspect, a mixture. Sometimes it’s really just a question of knowing “where that pocket of reducibility is”, which is something we can learn from education. But sometimes it’s a question of navigating a network of pockets, which may only be possible when brains reach a certain level of “computational ability”.
There’s another thing to discuss, related to education. And that’s the fact that over time, more and more “distinct pieces of knowledge” get built up in our civilization. There was perhaps a time in history when a brain of our size could realistically commit to memory at least the basics of much of that knowledge. But today that time has long passed. Yes, abstraction in effect compresses what one needs to know. But the continual addition of new and seemingly important knowledge, across countless specialties, makes it impossible for brains of our size to keep up.
Plenty of that knowledge is, though, quite siloed in different areas. But sometimes there are “grand analogies” to make—say pulling an idea from relativity theory and applying it to biological evolution. In a sense such analogies reveal new abstractions—but to make them requires knowledge that spans many different areas. And that’s a place where bigger brains—or AIs—can potentially do something that’s in a fundamental way “beyond us”.
Will there always be such “grand analogies” to make? The general growth of knowledge is inevitably a computationally irreducible process. And within it there will inevitably be pockets of reducibility. But how often in practice will one actually encounter “long-range connections” across “knowledge space”? As a specific example one can look at metamathematics, where such connections are manifest in theorems that link seemingly different areas of mathematics. And this example leads one to realize that at some deep level grand analogies are in a sense inevitable. In the context of the ruliad, one can think of different domains of knowledge as corresponding to different parts. But the nature of the ruliad—encompassing as it does everything that is computationally possible—inevitably imbues it with a certain homogeneity, which implies that (as the Principle of Computational Equivalence might suggest) there must ultimately be a correspondence between different areas. In practice, though, this correspondence may be at a very “atomic” (or “formal”) level, far below the kinds of descriptions (based on pockets of reducibility) that we imagine brains normally use.
But, OK, will it always take an “expanding brain” to keep up with the “expanding knowledge” we have? Computational irreducibility guarantees that there’ll always in principle be “new knowledge” to be had—separated from what’s come before by irreducible amounts of computation. But then there’s the question of whether in the end we’ll care about it. After all, it could be that the knowledge we can add is so abstruse that it will never affect any practical decisions we have to make. And, yes, to some extent that’s true (which is why only some tiny fraction of the Earth’s population will care about what I’m writing here). But another consequence of computational irreducibility is that there will always be “surprises”—and those can eventually “push into focus” even what at first seems like arbitrarily obscure knowledge.
Language in general—and compositional language in particular—is arguably the greatest invention of our species. But is it somehow “the top”—the highest possible representation of things? Or if, for example, we had bigger brains, is there something beyond it that we could reach?
Well, in some very formal sense, yes, compositional language (at least in idealized form) is “the top”. Because—at least if it’s allowed to include utterances of any length—then in some sense it can in principle encode arbitrary, universal computations. But this really isn’t true in any useful sense—and indeed to apply ordinary compositional language in this way would require doing computationally irreducible computations.
So we return to the question of what might in practice lie beyond ordinary human language. I wondered about this for a long time. But in the end I realized that the most important clue is in a sense right in front of me: the concept of computational language, that I’ve spent much of my life exploring.
It’s worth saying at the outset that the way computational language plays out for computers and for brains is somewhat different, and in some respects complementary. In computers you might specify something as a Wolfram Language symbolic expression, and then the “main action” is to evaluate this expression, potentially running a long computation to find out what the expression evaluates to.
Brains aren’t set up to do long computations like this. For them a Wolfram Language expression is something to use in effect as a “representation of a thought”. (And, yes, that’s an important distinction between the computational language concept of Wolfram Language, and standard “programming languages”, which are intended purely as a way to tell a computer what to do, not a way to represent thoughts.)
So what kinds of thoughts can we readily represent in our computational language? There are ones involving explicit numbers, or mathematical expressions. There are ones involving cities and chemicals, and other real-world entities. But then there are higher-level ones, that in effect describe more abstract structures.
For example, there’s NestList, which gives the result of nesting any operation, here named f:
At the outset, it’s not obvious that this would be a useful thing to do. But in fact it’s a very successful abstraction: there are lots of functions f for which one wants to do this.
In the development of ordinary human language, words tend to get introduced when they’re useful, or, in other words, when they express things one often wants to express. But somehow in human language the words one gets tend to be more concrete. Maybe they describe something that directly happens to objects in the world. Maybe they describe our impression of a human mental state. Yes, one can make rather vague statements like “I’m going to do something to someone”. But human language doesn’t normally “go meta”, doing things like NestList where one’s saying that one wants to take some “direct statement” and in effect “work with the statement”. In some sense, human language tends to “work with data”, applying a simple analog of code to it. Our computational language can “work with code” as “raw material”.
One can think about this as a “higher-order function”: a function that operates not on data, but on functions. And one can keep going, dealing with functions that operate on functions that operate on functions, and so on. And at every level one is increasing the generality—and abstraction—at which one is working. There may be many specific functions (a bit analogous to verbs) that operate on data (a bit analogous to nouns). But when we talk about operating on functions themselves we can potentially have just a single function (like NestList) that operates, quite generally, on many functions. In ordinary language, we might call such things “metaverbs”, but they aren’t something that commonly occurs.
But what makes them possible in computational language? Well, it’s taking the computational paradigm seriously, and representing everything in computational terms: objects, actions, etc. In Wolfram Language, it’s that we can represent everything as a symbolic expression. Arrays of numbers (or countries, or whatever) are symbolic expressions. Graphics are symbolic expressions. Programs are symbolic expressions. And so on.
And given this uniformity of representation it becomes feasible—and natural—to do higher-order operations, that in effect manipulate symbolic structure without being concerned about what the structure might represent. At some level we can view this as leading to the ultimate abstraction embodied in the ruliad, where in a sense “everything is pure structure”. But in practice in Wolfram Language we try to “anchor” what we’re doing to known concepts from ordinary human language—so that we use names for things (like NestList) that are derived from common English words.
In some formal sense this isn’t necessary. Everything can be “purely structural”, as it is not only in the ruliad but also in constructs like combinators, where, say, the operation of addition can be represented by:
Combinators have been around for more than a century. But they are almost impenetrably difficult for most humans to understand. Somehow they involve too much “pure abstraction”, not anchored to concepts we “have a sense of” in our brains.
It’s been interesting for me to observe over the years what it’s taken for people (including myself) to come to terms with the kind of higher-order constructs that exist in the Wolfram Language. The typical pattern is that over the course of months or years one gets used to lots of specific cases. And only after that is one able—often in the end rather quickly—to “get to the next level” and start to use some generalized, higher-order construct. But normally one can in effect only “go one level at a time”. After one groks one level of abstraction, that seems to have to “settle” for a while before one can go on to the next one.
Somehow it seems as if one is gradually “feeling out” a certain amount of computational irreducibility, to learn about a new pocket of reducibility, that one can eventually use to “think in terms of”.
Could “having a bigger brain” speed this up? Maybe it’d be useful to be able to remember more cases, and perhaps get more into “working memory”. But I rather suspect that combinators, for example, are in some sense fundamentally beyond all brain-like systems. It’s much as the Principle of Computational Equivalence suggests: one quickly “ascends” to things that are as computationally sophisticated as anything—and therefore inevitably involve computational irreducibility. There are only certain specific setups that remain within the computationally bounded domain that brain-like systems can deal with.
Of course, even though they can’t directly “run code in their brains”, humans—and LLMs—can perfectly well use Wolfram Language as a tool, getting it to actually run computations. And this means they can readily “observe phenomena” that are computationally irreducible. And indeed in the end it’s very much the same kind of thing observing such phenomena in the abstract computational universe, and in the “real” physical universe. And the point is that in both cases, brain-like systems will pull out only certain features, essentially corresponding to pockets of computational reducibility.
How do things like higher-order functions relate to this? At this point it’s not completely clear. Presumably in at least some sense there are hierarchies of higher-order functions that capture certain kinds of regularities that can be thought of as associated with networks of computational reducibility. And it’s conceivable that category theory and its higher-order generalizations are relevant here. In category theory one imagines applying sequences of functions (“morphisms”) and it’s a foundational assumption that the effect of any sequence of functions can also be represented by just a single function—which seems tantamount to saying that one can always “jump ahead”, or in other words, that everything one’s dealing with is computationally reducible. Higher-order category theory then effectively extends this to higher-order functions, but always with what seem like assumptions of computational reducibility.
And, yes, this all seems highly abstract, and difficult to understand. But does it really need to be, or is there some way to “bring it down” to a level that’s close to everyday human thinking? It’s not clear. But in a sense the core art of computational language design (that I’ve practiced so assiduously for nearly half a century) is precisely to take things that at first might seem abstruse, and somehow cast them into an accessible form. And, yes, this is something that’s about as intellectually challenging as anything—because in a sense it involves continually trying to “figure out what’s really going on”, and in effect “drilling down” to get to the foundations of everything.
But, OK, when one gets there, how simple will things be? Part of that depends on how much computational irreducibility is left when one reaches what one considers to be “the foundations”. And part in a sense depends on the extent to which one can “find a bridge” between the foundations and something that’s familiar. Of course, what’s “familiar” can change. And indeed over the four decades that I’ve been developing the Wolfram Language quite a few things (particularly in areas like functional programming) that at first seemed abstruse and unfamiliar have begun to seem more familiar. And, yes, it’s taken the collective development and dissemination of the relevant ideas to achieve that. But now it “just takes education”; it doesn’t “take a bigger brain” to deal with these things.
One of the core features of the Wolfram Language is that it represents everything as a symbolic expression. And, yes, symbolic expressions are formally able to represent any kind of computational structure. But beyond that, the important point is that they’re somehow set up to be a match for how brains work.
And in particular, symbolic expressions can be thought of “grammatically” as consisting of nested functions that form a tree-like structure; effectively a more precise version of the typical kind of grammar that we find in human language. And, yes, just as we manage to understand and generate human language with a limited working memory, so (at least at the grammatical level) we can do the same thing with computational language. In other words, in dealing with Wolfram Language we’re leveraging our faculties with human language. And that’s why Wolfram Language can serve as such an effective bridge between the way we think about things, and what’s computationally possible.
But symbolic expressions represented as trees aren’t the only conceivable structures. It’s also possible to have symbolic expressions where the elements are nodes on a graph, and the graph can even have loops in it. Or one can go further, and start talking, for example, about the hypergraphs that appear in our Physics Project. But the point is that brain-like systems have a hard time processing such structures. Because to keep track of what’s going on they in a sense have to keep track of multiple “threads of thought”. And that’s not something individual brain-like systems as we current envision them can do.
As we’ve discussed several times here, it seems to be a key feature of brains that they create a single “thread of experience”. But what would it be like to have multiple threads? Well, we actually have a very familiar example of that: what happens when we have a whole collection of people (or other animals).
One could imagine that biological evolution might have produced animals whose brains maintain multiple simultaneous threads of experience. But somehow it has ended up instead restricting each animal to just one thread of experience—and getting multiple threads by having multiple animals. (Conceivably creatures like octopuses may actually in some sense support multiple threads within one organism.)
Within a single brain it seems important to always “come to a single, definite conclusion”—say to determine where an animal will “move next”. But what about in a collection of organisms? Well, there’s still some kind of coordination that will be important to the fitness of the whole population—perhaps even something as direct as moving together as a herd or flock. And in a sense, just as all those different neuron firings in one brain get collected to determine a “final conclusion for what to do”, so similarly the conclusions of many different brains have to be collected to determine a coordinated outcome.
But how can a coordinated outcome arise? Well, there has to be communication of some sort between organisms. Sometimes it’s rather passive (just watch what your neighbor in a herd or flock does). Sometimes it’s something more elaborate and active—like language. But is that the best one can do? One might imagine that there could be some kind of “telepathic coordination”, in which the raw pattern of neuron firings is communicated from one brain to another. But as we’ve argued, such communication cannot be expected to be robust. To achieve robustness, one must “package up” all the internal details into some standardized form of communication (words, roars, calls, etc.) that one can expect can be “faithfully unpacked” and in effect “understood” by other, suitably similar brains.
But it’s important to realize that the very possibility of such standardized communication in effect requires coordination. Because somehow what goes on in one brain has to be aligned with what goes on in another. And indeed the way that’s maintained is precisely through continual communication.
So, OK, how might bigger brains affect this? One possibility is that they might enable more complex social structures. There are plenty of animals with fairly small brains that successfully form “all do the same thing” flocks, herds and the like. But the larger brains of primates seem to allow more complex “tribal” structures. Could having a bigger brain let one successfully maintain a larger social structure, in effect remembering and handling larger numbers of social connections? Or could the actual forms of these connections be more complex? While human social connections seem to be at least roughly captured by social networks represented as ordinary graphs, maybe bigger brains would for example routinely require hypergraphs.
But in general we can say that language—or standardized communication of some form—is deeply connected to the existence of a “coherent society”. For without being able to exchange something like language there’s no way to align the members of a potential society. And without coherence between members something like language won’t be useful.
As in so many other situations, one can expect that the detailed interactions between members of a society will show all sorts of computational irreducibility. And insofar as one can identify “the will of society” (or, for that matter, the “tide of history”), it represents a pocket of computational reducibility in the system.
In human society there is a considerable tendency (though it’s often not successful) to try to maintain a single “thread of society”, in which, at some level, everyone is supposed to act more or less the same. And certainly that’s an important simplifying feature in allowing brains like ours to “navigate the social world”. Could bigger brains do something more sophisticated? As in other areas, one can imagine a whole network of regularities (or pockets of reducibility) in the structure of society, perhaps connected to a whole tower of “higher-order social abstractions”, that only brains bigger than ours can comfortably deal with. (“Just being friends” might be a story for the “small brained”. With bigger brains one might instead have patterns of dependence and connectivity that can only be represented in complicated graph theoretic ways.)
We humans have a tremendous tendency to think—or at least hope—that our minds are somehow “at the top” of what’s possible. But with what we know now about computation and how it operates in the natural world it’s pretty clear this isn’t true. And indeed it seems as if it’s precisely a limitation in the “computational architecture” of our minds—and brains—that leads to that most cherished feature of our existence that we characterize as “conscious experience”.
In the natural world at large, computation is in some sense happening quite uniformly, everywhere. But our brains seem to be set up to do computation in a more directed and more limited way—taking in large amounts of sensory data, but then filtering it down to a small stream of actions to take. And, yes, one can remove this “limitation”. And while the result may lead to more computation getting done, it doesn’t lead to something that’s “a mind like ours”.
And indeed in what we’ve done here, we’ve tended to be very conservative in how we imagine “extending our minds”. We’ve mostly just considered what might happen if our brains were scaled up to have more neurons, while basically maintaining the same structure. (And, yes, animals physically bigger than us already have larger brains—as did Neanderthals—but what we really need to look at is size of brain relative to size of the animal, or, in effect “amount of brain for a given amount of sensory input”.)
A certain amount about what happens with different scales of brains is already fairly clear from looking at different kinds of animals, and at things like their apparent lack of human-like language. But now that we have artificial neural nets that do remarkably human-like things we’re in a position to get a more systematic sense of what different scales of “brains” can do. And indeed we’ve seen a sequence of “capability thresholds” passed as neural nets get larger.
So what will bigger brains be able to do? What’s fairly straightforward is that they’ll presumably be able to take larger amounts of sensory input, and generate larger amounts of output. (And, yes, the sensory input could come from existing modalities, or new ones, and the outputs could go to existing “actuators”, or new ones.) As a practical matter, the more “data” that has to be processed for a brain to “come to a decision” and generate an output, the slower it’ll probably be. But as brains get bigger, so presumably will the size of their working memory—as well as the number of distinct “concepts” they can “distinguish” and “remember”.
If the same overall architecture is maintained, there’ll still be just a single “thread of experience”, associated with a single “thread of communication”, or a single “stream of tokens”. At the size of brains we have, we can deal with compositional language in which “concepts” (represented, basically, as words) can have at least a certain depth of qualifiers (corresponding, say, to adjectival phrases). As brain size increases, we can expect there can both be more “raw concepts”—allowing fewer qualifiers—as well as more working memory to deal with more deeply nested qualifiers.
But is there something qualitatively different that can happen with bigger brains? Computational language (and particularly my experience with the Wolfram Language) gives some indications, the most notable of which is the idea of “going meta” and using “higher-order constructs”. Instead of, say, operating directly on “raw concepts” with (say, “verb-like”) “functions”, we can imagine higher-order functions that operate on functions themselves. And, yes, this is something of which we see powerful examples in the Wolfram Language. But it feels as if we could somehow go further—and make this more routine—if our brains in a sense had “more capacity”.
To “go meta” and “use higher-order constructs” is in effect a story of abstraction—and of taking many disparate things and abstracting to the point where one can “talk about them all together”. The world at large is full of complexity—and computational irreducibility. But in essence what makes “minds like ours” possible is that there are pockets of computational reducibility to be found. And those pockets of reducibility are closely related to being able to successfully do abstraction. And as we build up towers of abstraction we are in effect navigating through networks of pockets of computational reducibility.
The progress of knowledge—and the fact that we’re educated about it—lets us get to a certain level of abstraction. And, one suspects, the more capacity there is in a brain, the further it will be able to go.
But where will it “want to go”? The world at large—full as it is with computational irreducibility, along with infinite numbers of pockets of reducibility—leaves infinite possibilities. And it is largely the coincidence of our particular history that defines the path we have taken.
We often identify our “sense of purpose” with the path we will take. And perhaps the definiteness of our belief in purpose is related to the particular feature of brains that leads us to concentrate “everything we’re thinking” down into just a single stream of decisions and action.
And, yes, as we’ve discussed, one could in principle imagine “multiway minds” with multiple “threads of consciousness” operating at once. But we humans (and individual animals in general) don’t seem to have those. Of course, in collections of humans (or other animals) there are still inevitably multiple “threads of consciousness” —and it’s things like language that “knit together” those threads to, for example, make a coherent society.
Quite what that “knitting” looks like might change as we scale up the size of brains. And so, for example, with bigger brains we might be able to deal with “higher-order social structures” that would seem alien and incomprehensible to us today.
So what would it be like to interact with a “bigger brain”? Inside, that brain might effectively use many more words and concepts than we know. But presumably it could generate at least a rough (“explain-like-I’m-5”) approximation that we’d be able to understand. There might well be all sorts of abstractions and “higher-order constructs” that we are basically blind to. And, yes, one is reminded of something like a dog listening to a human conversation about philosophy—and catching only the occasional “sit” or “fetch” word.
As we’ve discussed several times here, if we remove our restriction to “brain-like” operation (and in particular to deriving a small stream of decisions from large amounts of sensory input) we’re thrown into the domain of general computation, where computational irreducibility is rampant, and we can’t in general expect to say much about what’s going on. But if we maintain “brain-like operation”, we’re instead in effect navigating through “networks of computational reducibility”, and we can expect to talk about things like concepts, language and towers of abstraction.
From a foundational point of view, we can imagine any mind as in effect being at a particular place in the ruliad. When minds communicate, they are effectively exchanging the rulial analog of particles—robust concepts that are somehow unchanged as they propagate within the ruliad. So what would happen if we had bigger brains? In a sense it’s a surprisingly “mechanical” story: a bigger brain—encompassing more concepts, etc.—in effect just occupies a larger region of rulial space. And the presence of abstraction—perhaps learned from a whole arc of intellectual history—can lead to more expansion in rulial space.
And in the end it seems that “minds beyond ours” can be characterized by how large the regions of the ruliad they occupy are. (Such minds are, in some very literal rulial sense, more “broad minded”.) So what is the limit of all this? Ultimately, it’s a “mind” that spans the whole ruliad, and in effect incorporates all possible computations. But in some fundamental sense this is not a mind like ours, not least because by “being everything” it “becomes nothing”—and one can no longer identify it as having a coherent “thread of individual existence”.
And, yes, the overall thrust of what we’ve been saying applies just as well to “AI minds” as to biological ones. If we remove restrictions like being set up to generate the next token, we’ll be left with a neural net that’s just “doing computation”, with no obvious “mind-like purpose” in sight. But if we make neural nets do typical “brain-like” tasks, then we can expect that they too will find and navigate pockets of reducibility. We may well not recognize what they’re doing. But insofar as we can, then inevitably we’ll mostly be sampling the parts of “minds beyond ours” that are aligned with “minds like ours”. And it’ll take progress in our whole human intellectual edifice to be able to fully appreciate what it is that minds beyond ours can do.
Thanks for recent discussions about topics covered here in particular to Richard Assar, Joscha Bach, Kovas Boguta, Thomas Dullien, Dugan Hammock, Christopher Lord, Fred Meinberg, Nora Popescu, Philip Rosedale, Terry Sejnowski, Hikari Sorensen, and James Wiles.